Тогда из второго уравнения находим вначале

.

Из первого уравнения

.

Рассмотрим узел 3.

Для этого узла уместно вспомнить правило: если в узел сходятся 4 усилия (стержня), попарно лежащие на одной прямой ( и ; 5(кн) и ), то усилия в этих стержнях равны между собой по величине и по знаку, т. е.

;

.

Следовательно, узел 3 мы не вырезаем.

Вырезаем узел 5 (рис. 17б).

;

,

или

.

;

,

или

.

Решая совместно полученные 2 уравнения

,

, находим:

,

.

Вырезаем узел 2 (рис. 18).

; .

; .

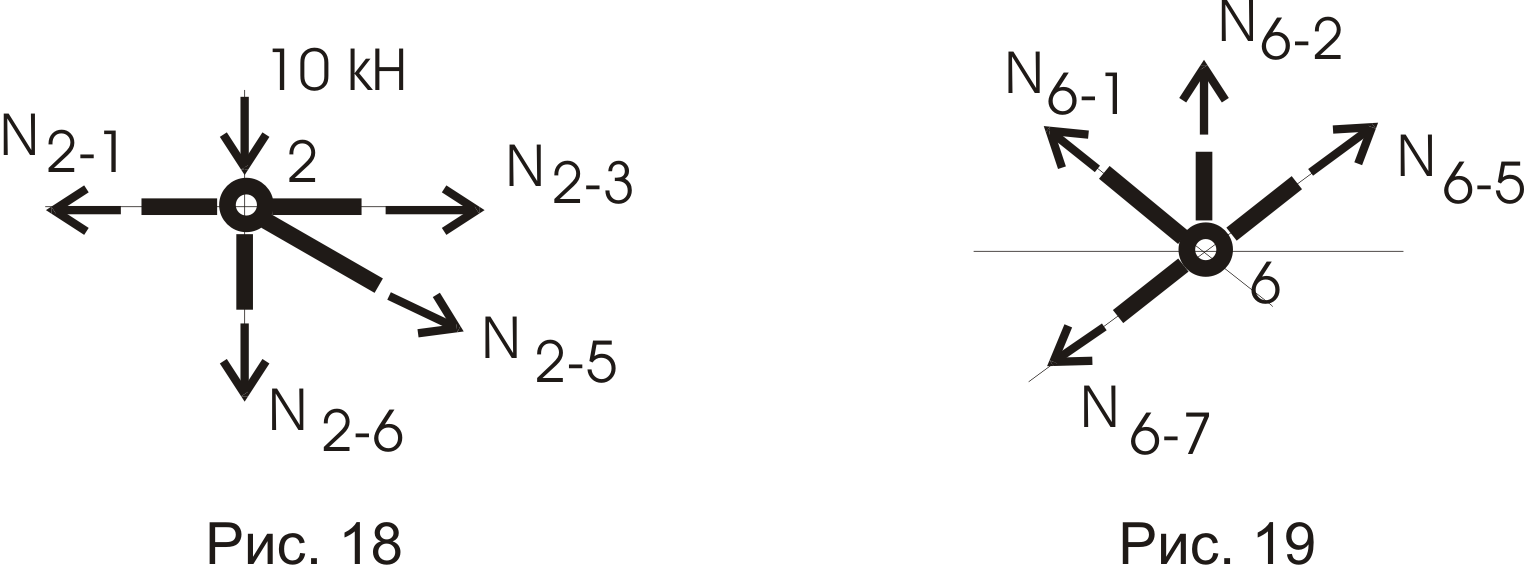
Из первого уравнения определяем

.

Из второго:

.

Узел 6 (рис. 19).

; ,

или

.

.

; ,

или

.

Приведем подобные и получим:

;

.

Из решения полученной системы:

кн;

кн.

Узел 1 (рис. 20).

; ,

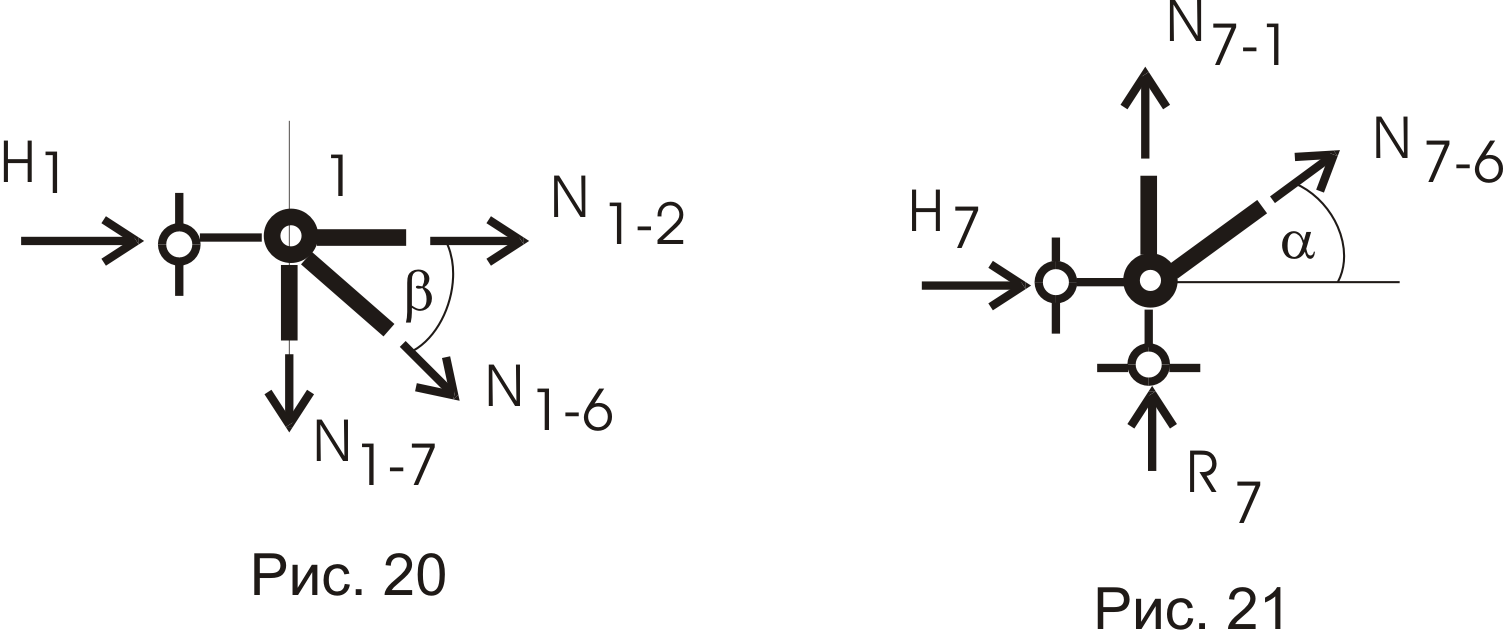
или

.

Направлением реакции Н₁ мы ошиблись.

; ,

или

.

Последний вырезается узел 7 (рис. 21).

; ;

(кн).

; ;

(кн).

Как видим, для консольной фермы опорные реакции могут определяться в последнюю очередь.

Способ сквозного сечения.

При таком подходе мы имеем три уравнения статического равновесия. Это позволяет проводить сечение, разрезая по трем неизвестным усилиям (стержням). Это могут быть сечения 1–1; 2–2; 3–3; 4–4; 5–5. Сечение 5-5 равносильно вырезанию узла 4.

Рассекая ферму, впоследствии можем рассматривать равновесие одной из ее полученных частей (правой или левой).

Сечение 1-1 (правая часть фермы – рис. 22).

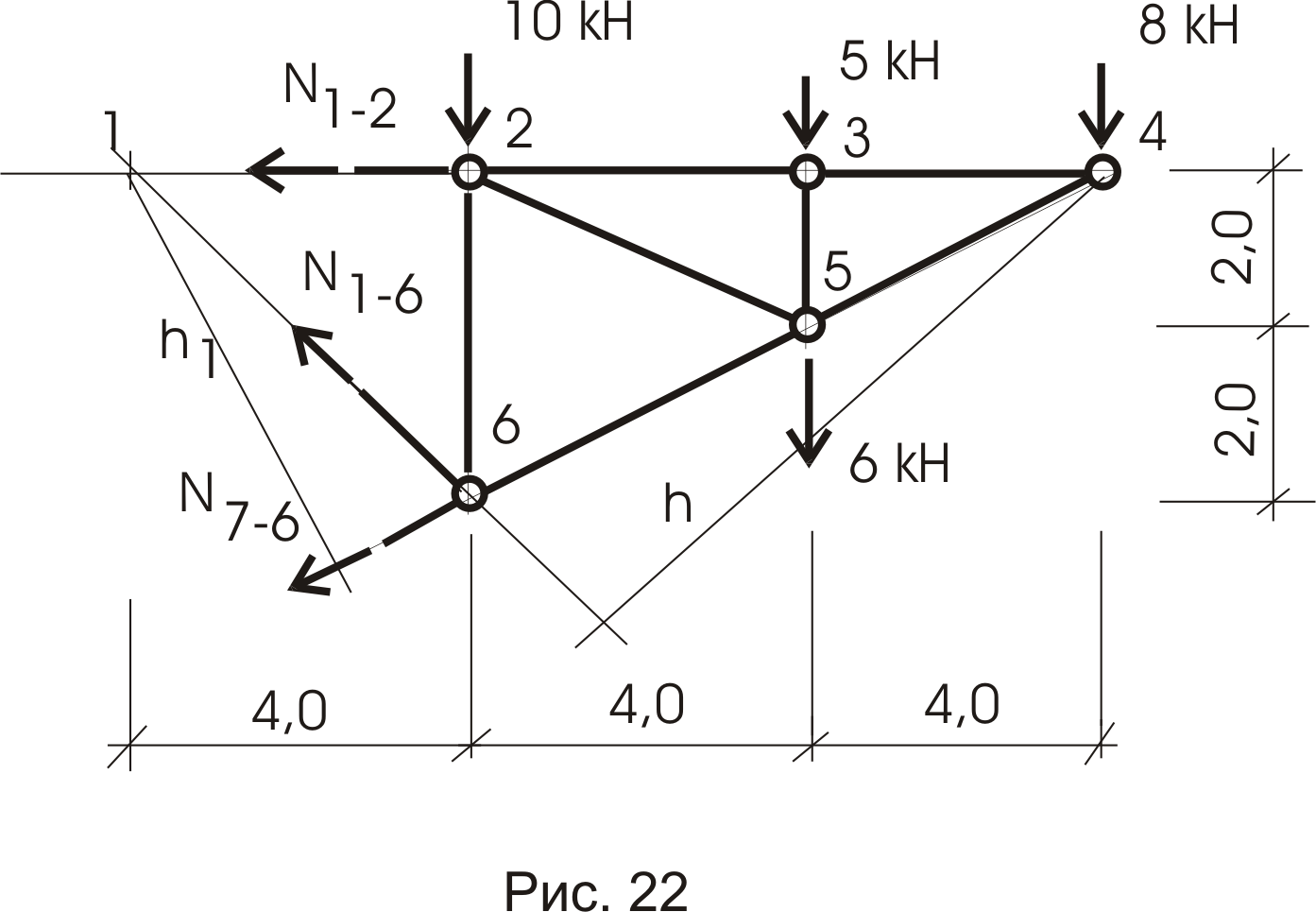
Используя одно из уравнений статики, определим искомое усилие.

Усилие

; ;

.

Усилие

; ;

. ( .

Усилие

; ;

(кн).

Сечение 2-2 (правая часть фермы - рис. 23).

Усилие нами уже определено из сечения 1-1.

Усилие

; ;

.

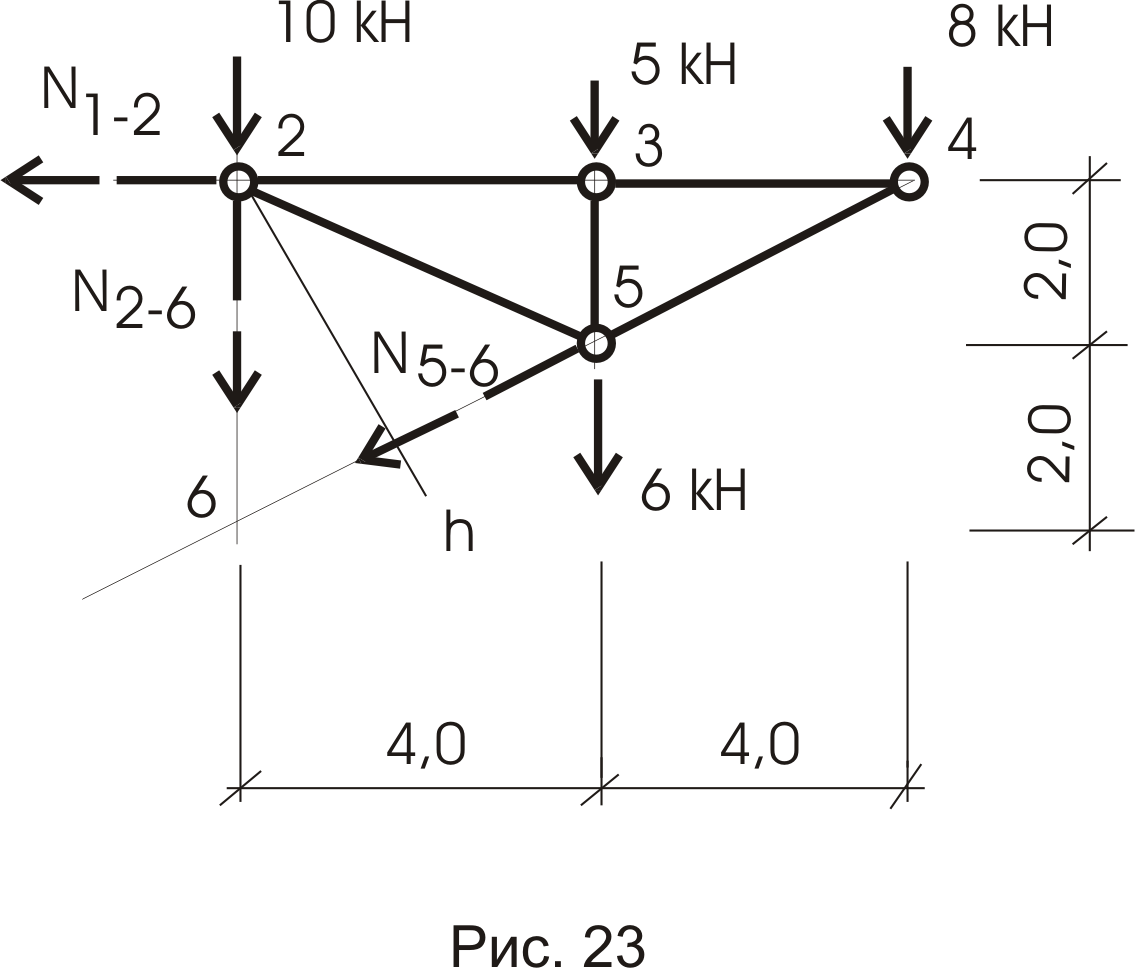
Усилие .

; ;

(кн).

Сечение 3-3 (вновь правая часть фермы – рис. 24).

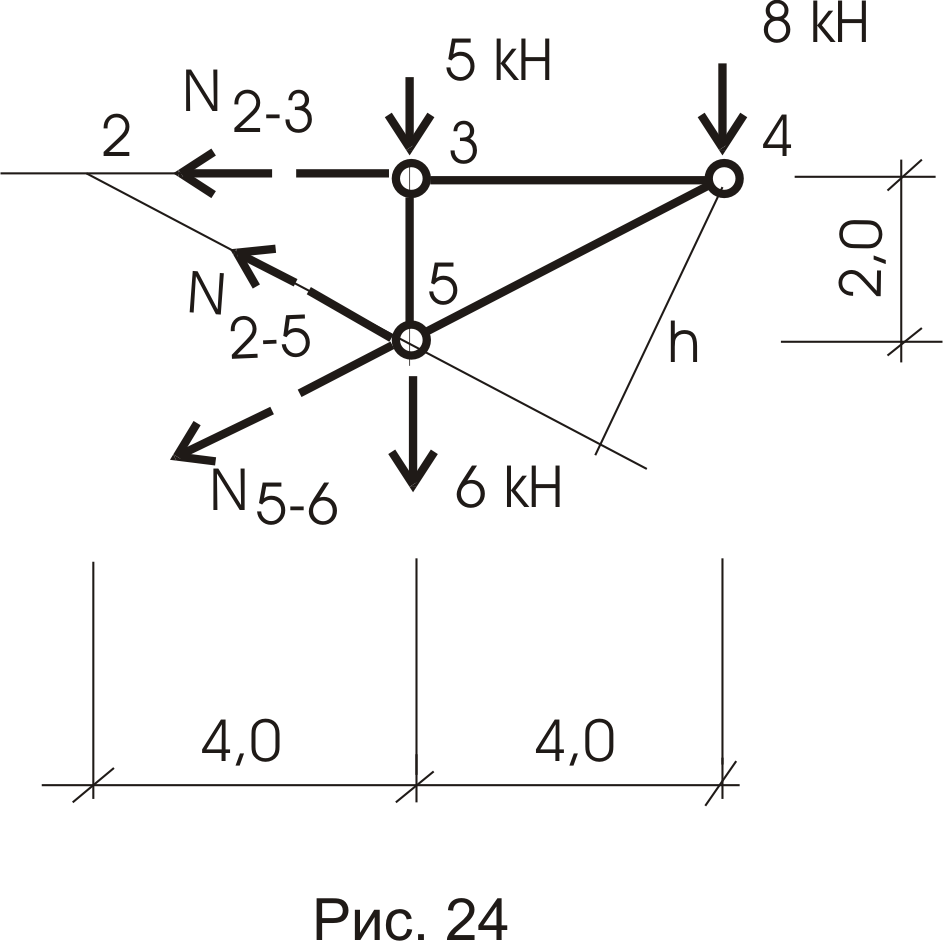
Усилие .

; ;

.

Усилие .

; ;

(кн).

Сравнивая значения усилий, вычисленные двумя способами, видим небольшую разницу, связанную с погрешностью вычислений (табл. 1).

Таблица 1

Усилия
Способ вырезания узлов	12,304	16,0	-30,194	-15,50	-41,752	14,612	27,0
Способ сквозного сечения	12,304	16,0	-30,20	-15,50	-41,759	14,615	27,0

1.3 Многодисковая рама (рис. 25)

Кинематический анализ дает:

Конструкция неизменяемая и неподвижная. Определение опорных реакций в связях (шарнирах) проведем расчленением конструкции на ее составляющие элементы (другие приемы здесь неприемлемы).

1 диск (элемент) – рис. 26а.

Составляем для 1 элемента уравнения статики:

; .

; .

; .

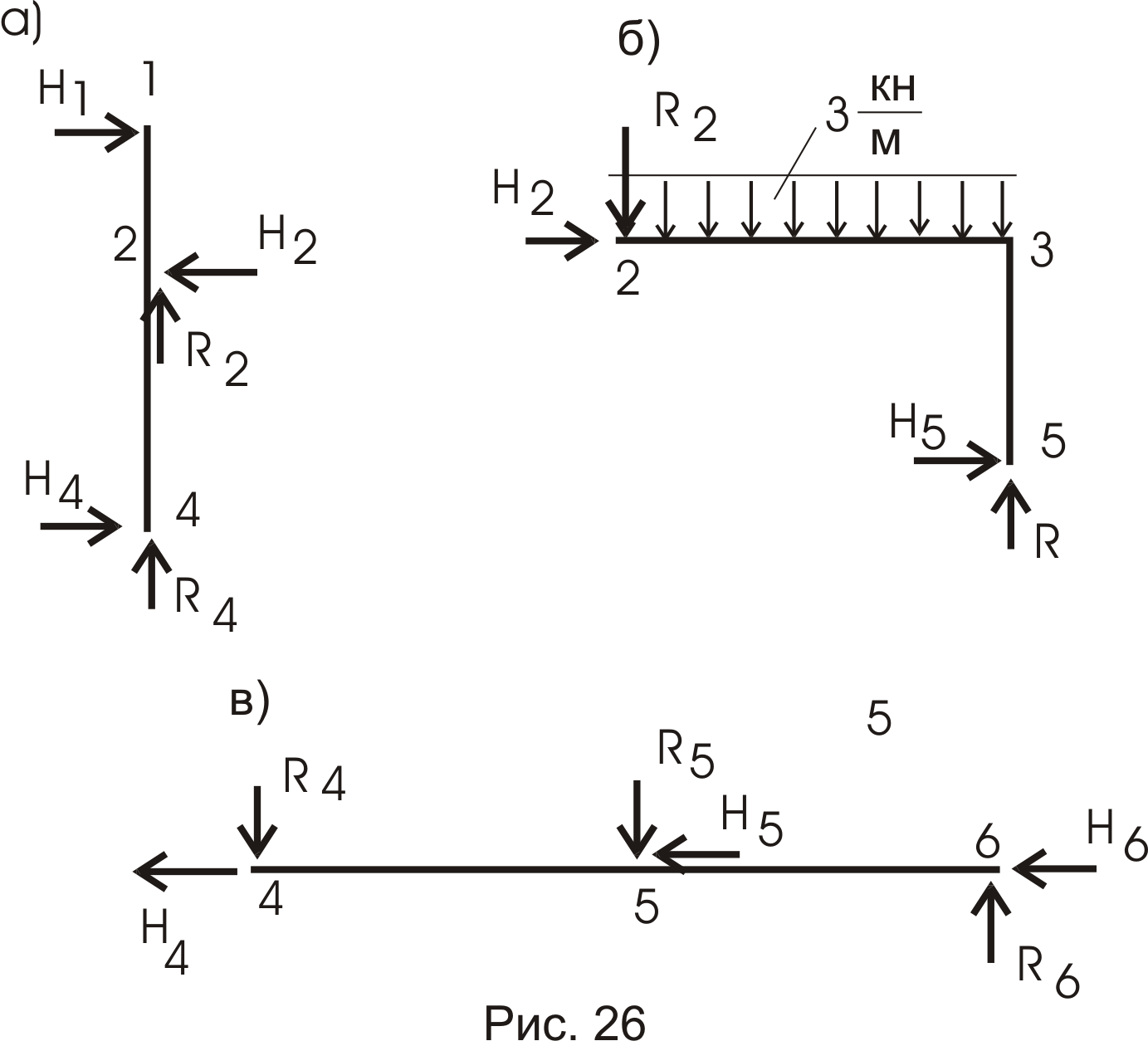
2 диск (элемент) – рис. 26б.

; .

; .

; .

3 диск (элемент) – рис. 26в.

; .

; .

; .

Систему уравнений представим в матричной форме:

.

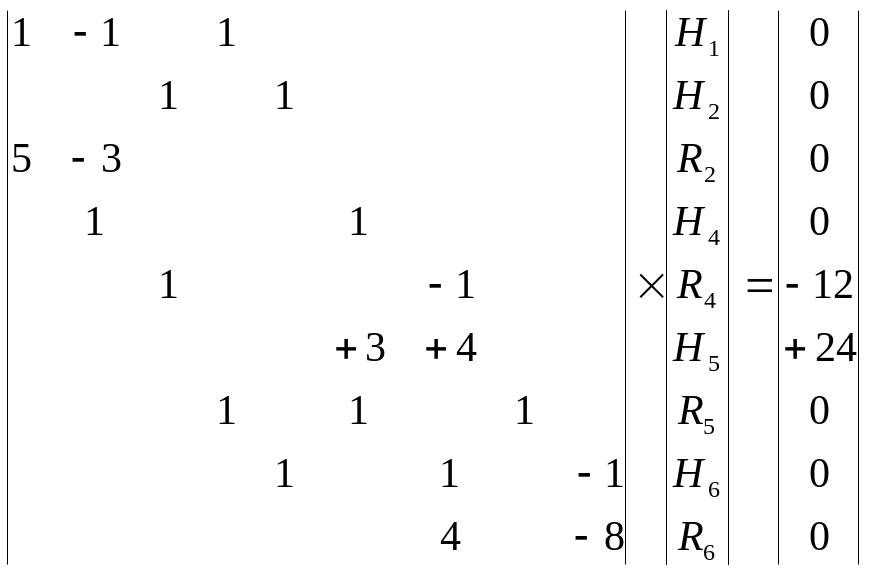Решение системы дает:

кн; кн; кн;

кн; кн; кн;

кн; кн; кн.

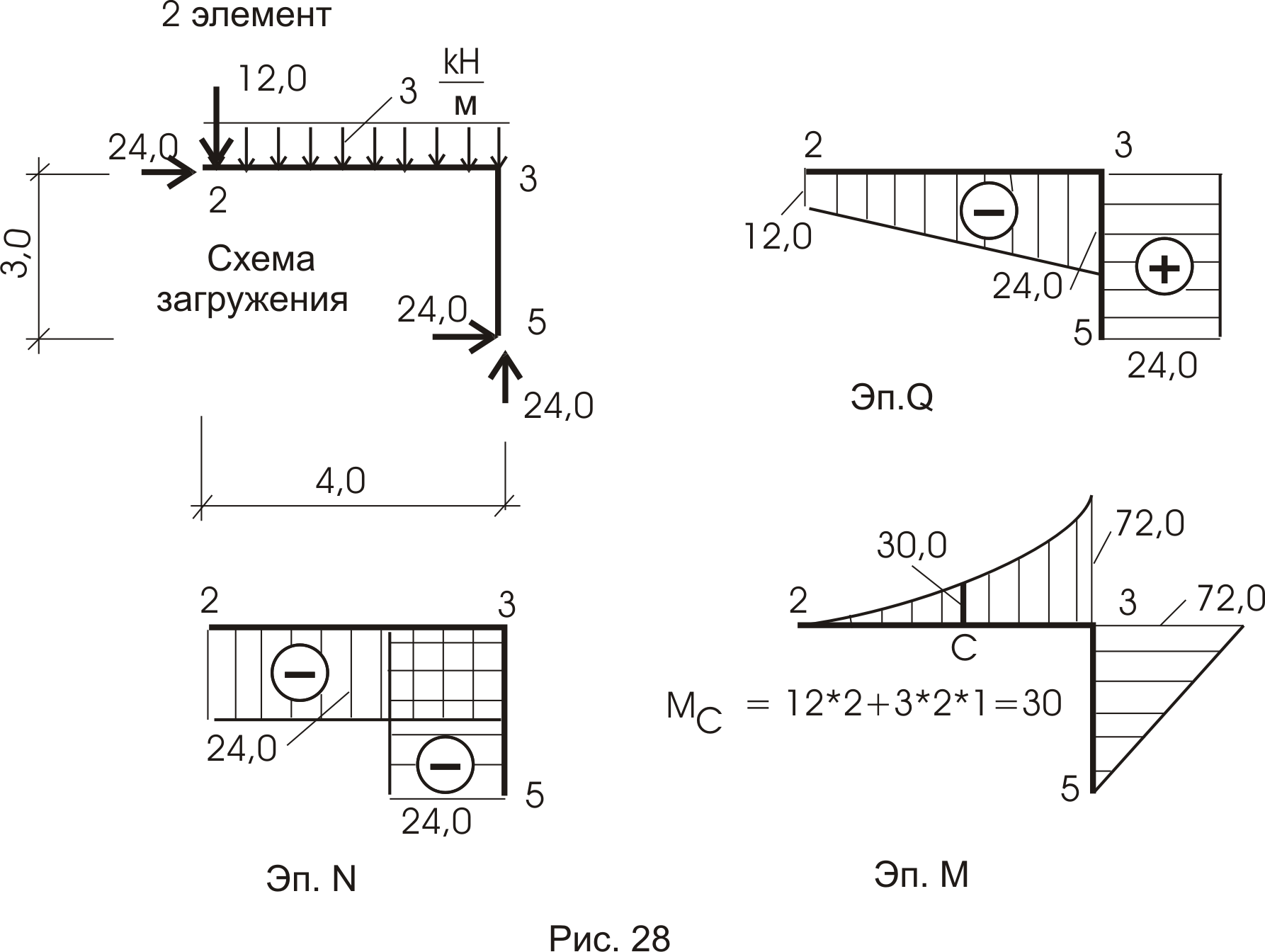
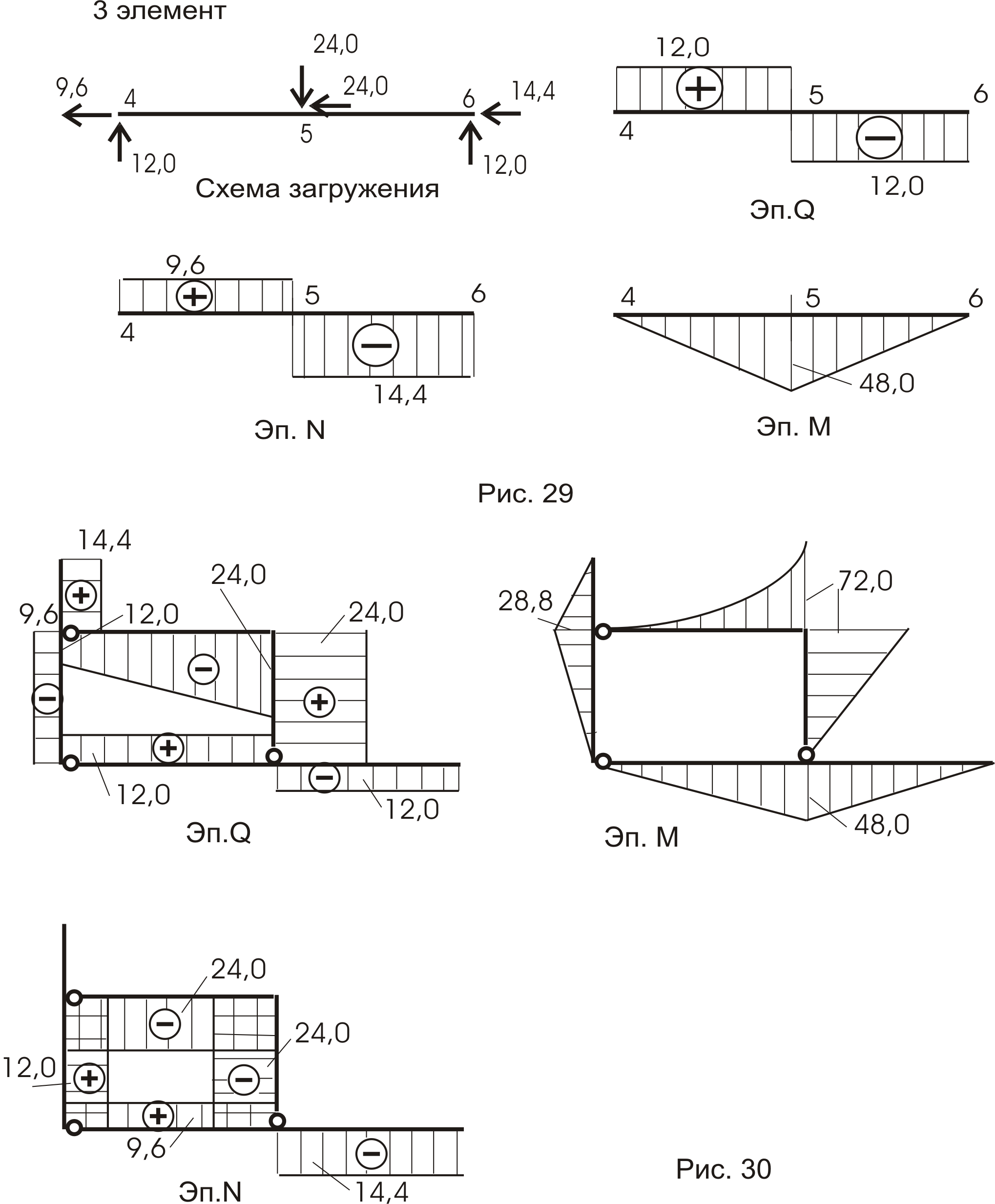
Эпюры внутренних усилий строим по элементам (рис. 27, 28, 29), а потом объединяем в одно целое (рис. 30). Нужно помнить, что в схемах загружения усилия в связях прикладываем с учетом их знака: если получили знак минус, то направление усилия меняем на противоположное.

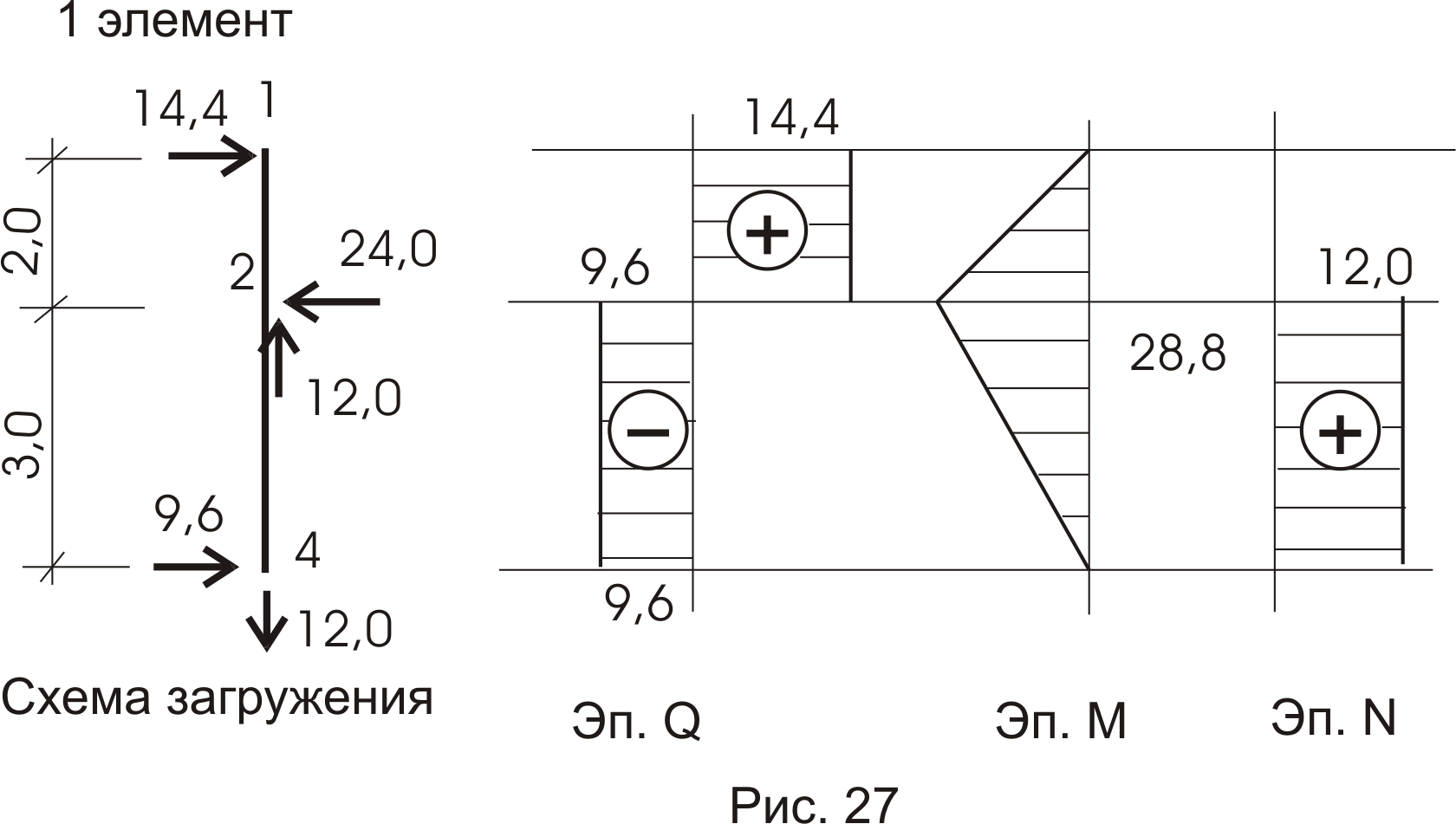
1.5 Комбинированная конструкция

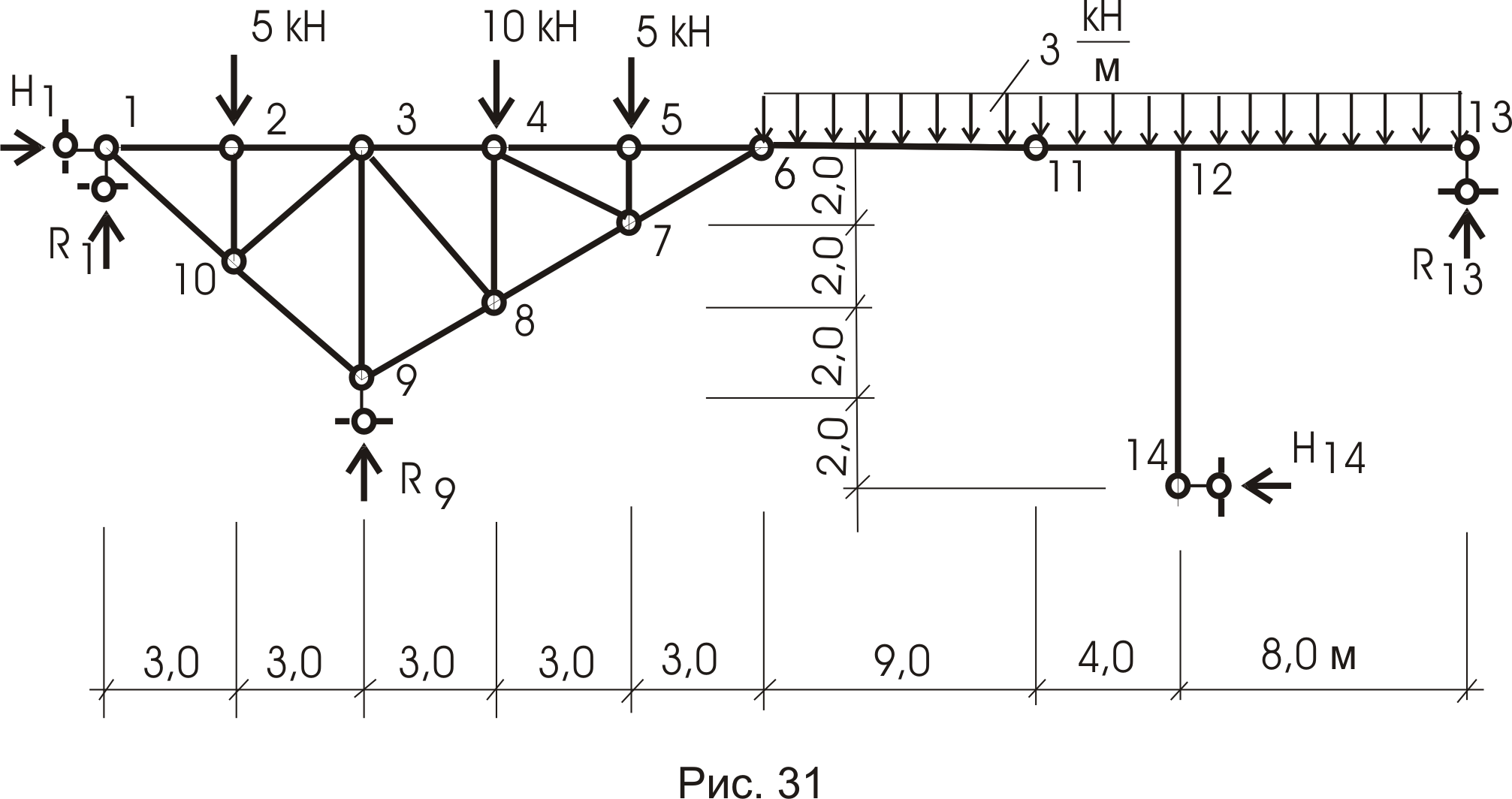
Комбинированные конструкции – конструкции, состоящие из сочетания рам, балок, ферм. Для примера рассмотрим конструкцию, показанную на рисунке 31 (конструкция мостового перехода).

Расчет:

1. Кинематический анализ.

Для конструкции в целом

.

.

Расчленим конструкцию на ее элементы:

1-ый элемент – ферма

.

Ферма - геометрически неизменяемая конструкция (диск), опирающаяся на 3 опорных стержня, следовательно, является основной конструкцией. Балка и рама (второй и третий элементы) крепятся к ферме с помощью связей – шарнирами 6 и 11.

2. Опорные реакции (усилия) в связях

Расчленим конструкцию на три элемента: ферму, балку, раму.

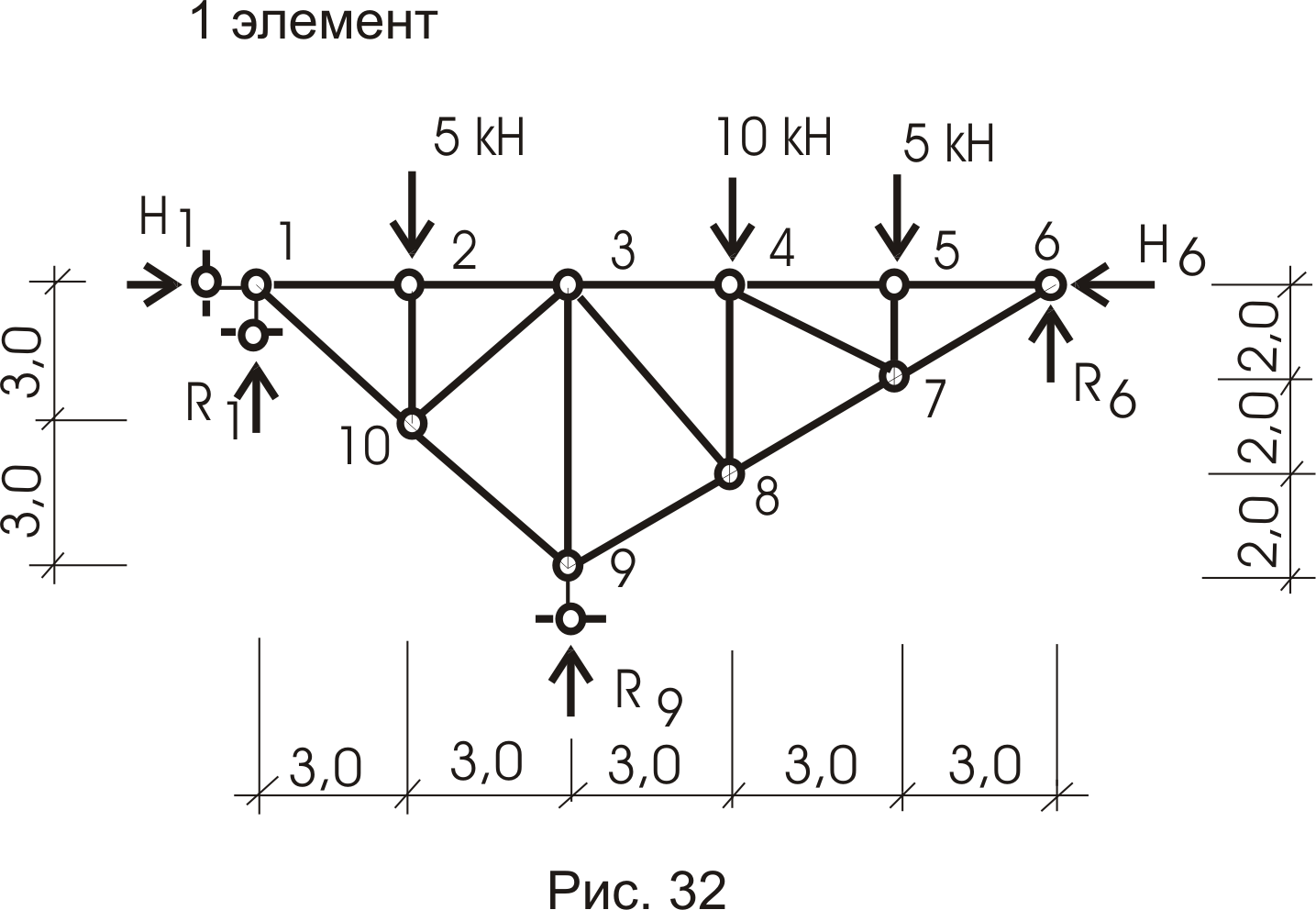
1- ый элемент (рис. 32)

; .

; или .

; или .

2 ой элемент (рис. 33а)

; .

; или (кн).

; .

Отсюда находим ; из 2 уравнения .

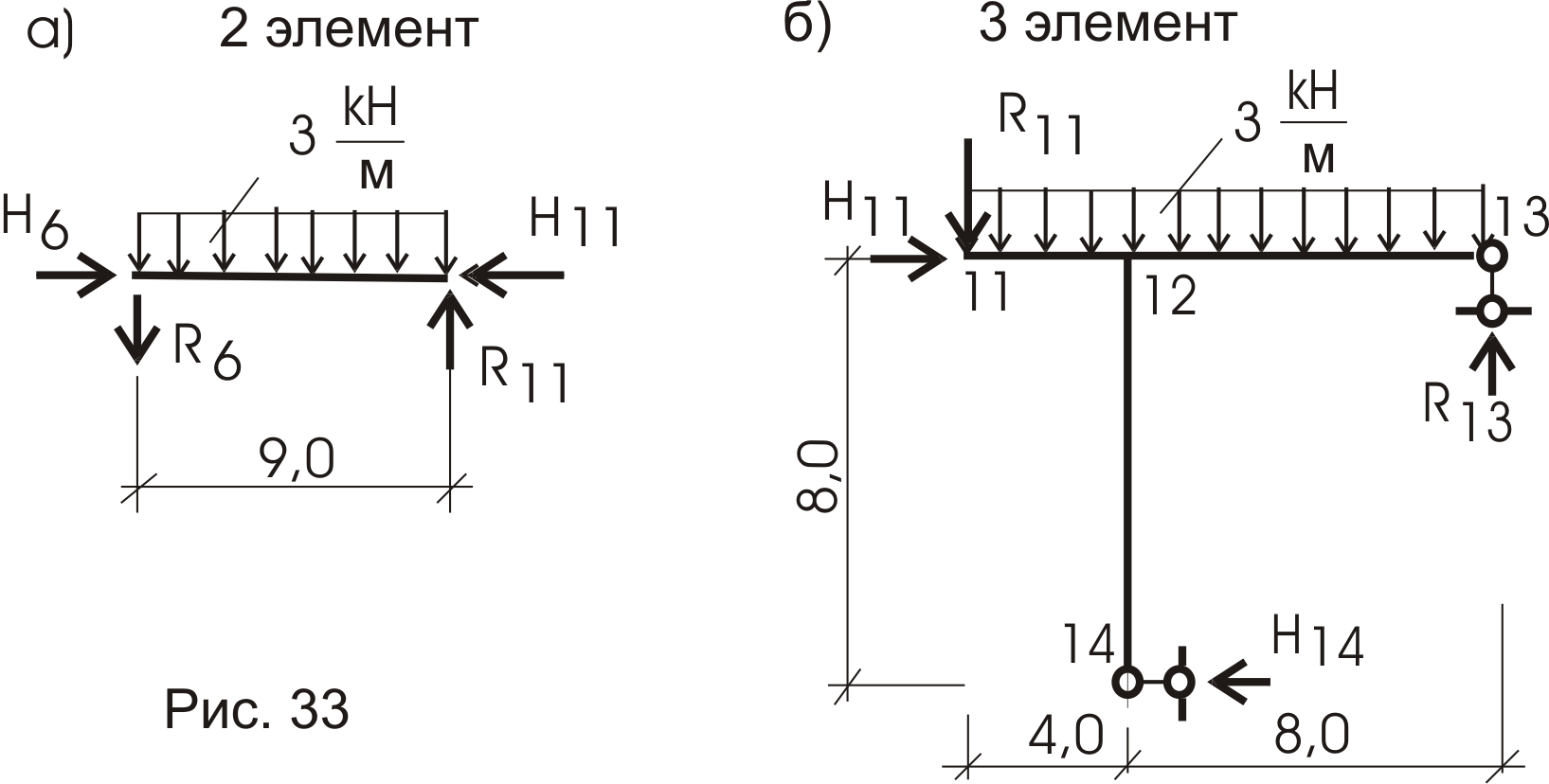
3-ий элемент (рис.33б)

; .

; или .

; .

Отсюда ; ; ; .

Усилия в связях 2 и 3 элементов определены, что позволит определить и усилия в связях 1 элемента:

.

Из третьего уравнения:

,

из второго:

; .

Знание усилий в связях позволяет одним из разобранных путей построить эпюры внутренних усилий в балке и раме (рис. 34) и определить усилия в стержнях фермы (таблица 2).

Таблица 2

стержень	1-2	2-3	3-4	4-5	5-6	6-7	7-8	8-9
величина усилия	-19,5	-19,5	-23,25	-26,98	-26,98	-24,32	-28,82	-36,31

стержень	9-10	1-10	2-10	3-10	3-9	3-8	4-8	4-7	5-7
величина усилия	-42,78	-39,25	-5	3,53	-10,85	10,44	-12,5	4,50	-5