Пример 1. Для конструкции (рамы - рис. 160) требуется :

Определить горизонтальное перемещение точки 1.

Решение задачи.

Строим эпюру М_изг. от внешней нагрузки (рис. 161).

Для построения определим вертикальные опорные реакции:

; ; отсюда находим

; , отсюда определяем .

.

2. Построим эпюру от единичного загружения (рис. 162).

3. Вычисляем искомое перемещение:

а) по правилу Верещагина

б) по правилу Симпсона

.

10. Перемещение от осадки опор

Рассмотрим пример (рис. 163):

Рама. Опора 4 просела на . Требуется определить горизонтальное перемещение узла 2. Загрузим узел 2 (рис. 163б) горизонтальной единичной нагрузкой. В опорных связях возникнут реакции (усилия).

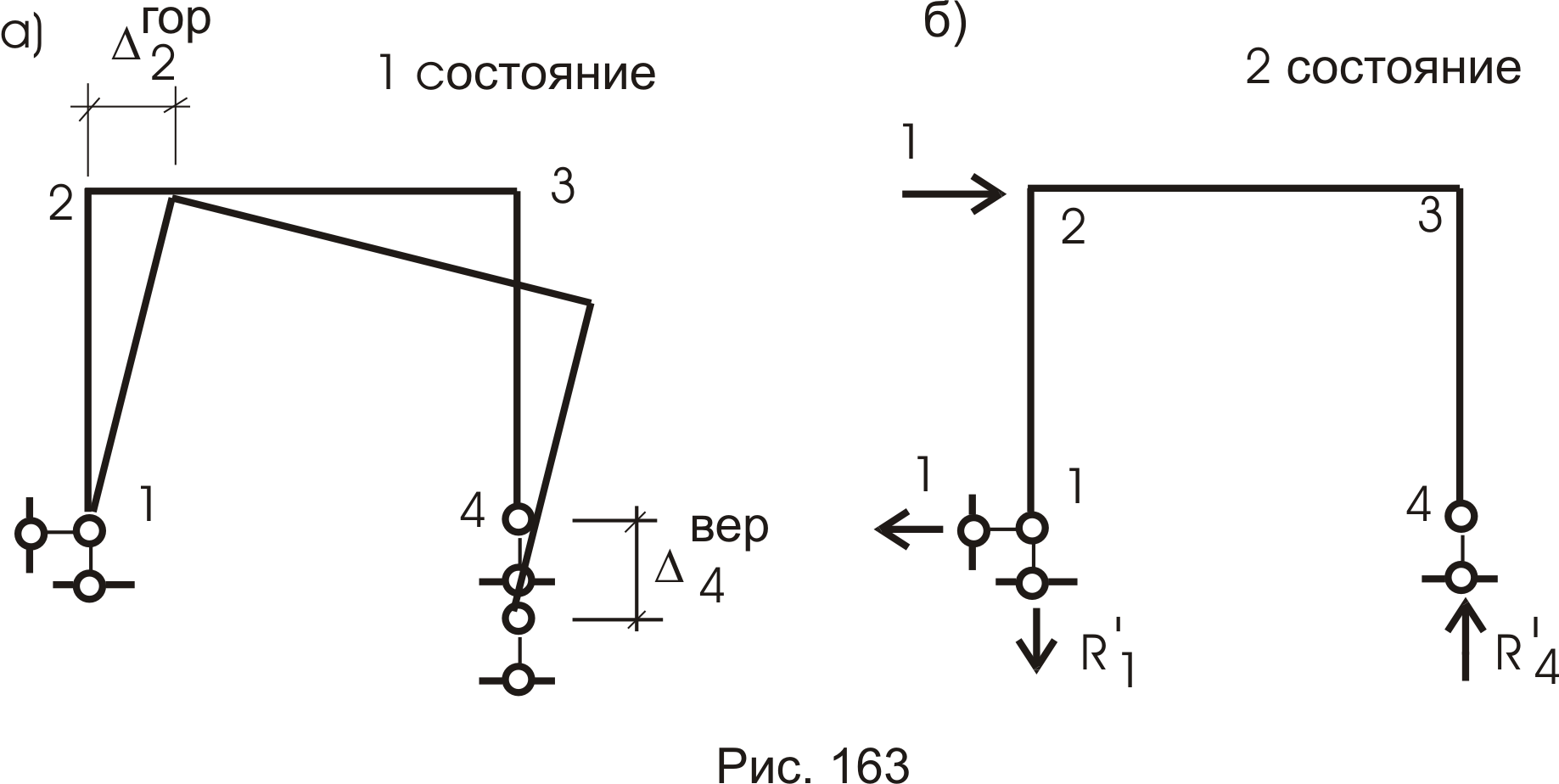
На основании теоремы о взаимности работ запишем:

.

Работа единичной силы (сил второго состояния) на перемещениях, вызванных осадкой опор (силами первого состояния), равна работе сил второго состояния (реакции связи) на перемещениях (осадка опор) первого состояния, т. е. перемещение в i-ом направлении вычисляется как сумма произведений реакций j связи (R_j⁽¹⁾) от единичного i-го загружения на величину перемещения j-ой связи (осадки опоры).

Пример (рис. 164). Определить угол поворота сечения 3, т е.

. .

11. Перемещение от воздействия температуры Запишем формулу перемещений Мора:

в этом выражении:

; ; - перемещения от внешних воздействий на сооружение (конструкцию). Внешним воздействием может быть и температурное воздействие.

Предположим, что элемент конструкции нагрет неравномерно.

Рассмотрим элементарный участок dx (рис. 165). С одной стороны его мысленно закрепим глухой заделкой. От воздействия температуры волокна удлиняются (укорачиваются), вызывая деформацию стержня.

; ; ;

; - коэффициент линейного расширения.

Тогда

; ;

.

Следует заметить, что оба слагаемых равноправны.

.

Внимание. Правило знаков:

а) для М

Изгибающие моменты откладываем на растянутых волокнах. Если воздействие температуры и единичная сила растягивают волокна стержня с одной стороны относительно оси - знак вычисления положительный.

б) для N

Если единичное усилие и температурное воздействие растягивают (сжимают) стержень - знак произведения положительный.

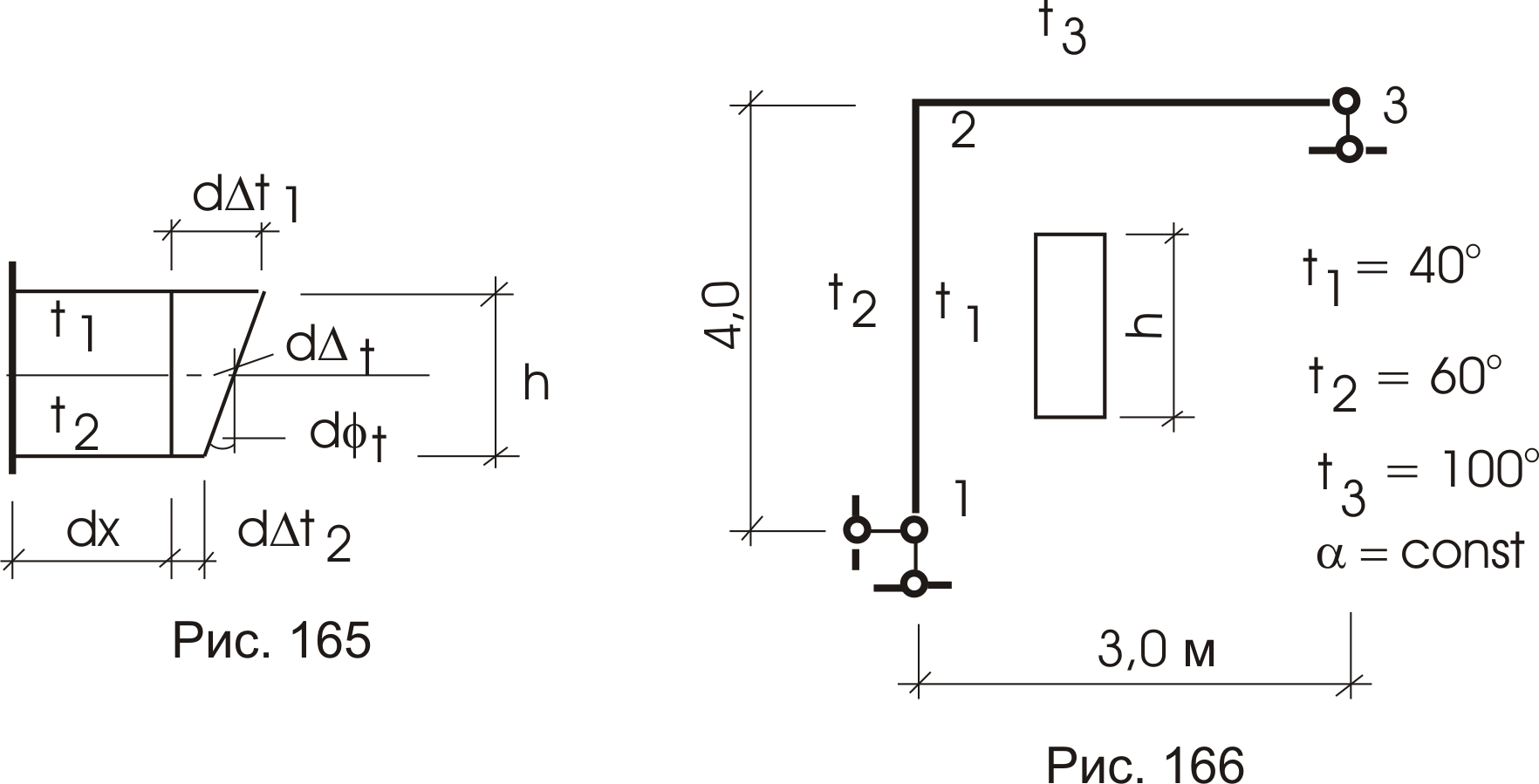
Пример (рис. 166).

Определить горизонтальное перемещение узла 3.

Решение.

Приложим к узлу 3 единичную силу. Построим эпюры М₁ (рис. 167б) и N₁ (рис. 167в). Вычислим перемещение перемножением эпюр.

.

9. Статически неопределимые

системы (конструкции)

1. Общие понятия.

Статически неопределимые системы – это системы, у которых внутренние усилия (в первую очередь, опорные реакции) не могут быть определены из уравнений статики. Для таких конструкций характерно, что степень свободы n – отрицательное число, т. е.

.

Это означает, что конструкция имеет избыточное число связей, обеспечивающих ее неподвижность и неизменяемость.

Ряд примеров.

1. Балка (рис. 168)

Балка имеет 2 избыточные связи.

2. Ферма (рис. 169)

или для ферм

Подсчет по любой формуле дает, что ферма имеет 2 избыточные связи.

3. Рама (рис. 170)

Рама имеет 3 избыточные связи.

2. Методы расчета статически неопределимых

систем (конструкций)

Расчет любой конструкции сводится к определению, как мы уже знаем, внутренних усилий в элементах конструкций. И в начале расчета определяем реакции в связях. В статически определимых конструкциях используем уравнения статики. В статически неопределимых конструкциях этих уравнений недостаточно. Встает вопрос: какие дополнительные уравнения использовать? Если мы зададимся целью вначале определить усилия в избыточных связях – мы придем к методу сил.

Под действием внешней нагрузки точки (сечения) конструкции перемещаются. Связь между этими перемещениями и усилиями в общем виде в упругой стадии имеет вид:

,

где - перемещение сечения конструкции; - коэффициент пропорциональности; - усилия (это может быть M, Q, N).

Если мы зададимся целью определить перемещения заданных точек (узлов) конструкции, мы придем к методу перемещений.

Эти два основных метода с середины 18 века являются основными методами и не утратили свого значения в наши дни.

В недалеком прошлом (порядка 30 лет) в практике расчета конструкций начал использоваться метод конечных элементов (МКЭ), в котором одновременно определяются и усилия, и перемещения.

3. Метод сил

Наша цель – определить усилия в избыточных связях. Вначале мы должны назначить для расчета избыточные связи и освободиться от них (удалить их). Получаем расчетную модель конструкции, названную нашими предками – «основная система». Оставим этот термин за расчетной моделью.

Основная система метода сил

Выбор основной системы зависит от расчетчика (его опыта), и она, как мы отметили чуть выше, получается путем отбрасывания избыточного числа связей. К основной системе предъявляются требования:

• не должна быть изменяемой и мгновенно изменяемой;

• должна быть статически определимой.

Для ряда примеров рассмотрим выбор основной системы.

Балка (рис.171)

.

Одна избыточная связь.

Вариант а) Ввели шарнир в произвольное сечение, помня, что шарнир уменьшает одну связь.

Варианты б) и в) равнозначны. Во всех случаях мы получили неизменяемые конструкции и статически определимые.

Вариант г) не может быть принят в качестве основной системы, так как полученная система мгновенно изменяемая; все три опорных стержня пересекаются в бесконечности.

Разобранный пример дает понятия о:

• абсолютно необходимых связях, которые при выборе основной системы нельзя убрать;

• условно необходимых связях, которые можно убрать, не нарушая геометрическую неизменяемость и неподвижность основной системы.

Ферма (рис. 172)

.

Ферма имеет одну избыточную связь или, как говорится, однажды статически неопределимая ферма. Присмотримся к ферме и можем отметить:

• опорные реакции определяются из уравнений статики;

• усилия в стержнях 3 – 4; 4 – 5; 5 – 6; 4 – 6 могут быть определены вырезанием узлов или сквозным сечением. Следовательно, опорные стержни и перечисленные стержни являются абсолютно необходимыми;

• усилия в стержнях 1 – 2; 1 – 3; 1 – 6; 2 – 3; 2 – 6; 3 – 6 не могут быть определены обычными методами. Их можем считать условно необходимыми – один из них можем отбросить, тогда система будет статически определима и геометрически неизменяема (рис. 172б).

Разобранные примеры дают понятия о внешней статической неопределимости (внешние связи) и внутренней статической неопределимости (внутренние связи).

Наглядным примером внутренней неопределимости является замкнутая рама (замкнутый контур) (рис. 173):

.

Усилия во внешних связях (опорные реакции) определяются из уравнений статики, а внутренние усилия M, Q, N мы не определим, пока не разрежем в любом сечении контур (рис.174). Нарушая жесткое соединение равнозначно удаленных 3-х внутренних связей, получаем три неизвестных усилия. Можем сделать вывод, что каждый замкнутый контур рамы дает нам три неизвестных усилия и степень статической неопределимости m может подсчитываться для замкнутых контуров:

где: K – количество замкнутых контуров;

Ш – количество простых шарниров в контурах (рис. 175).

где .

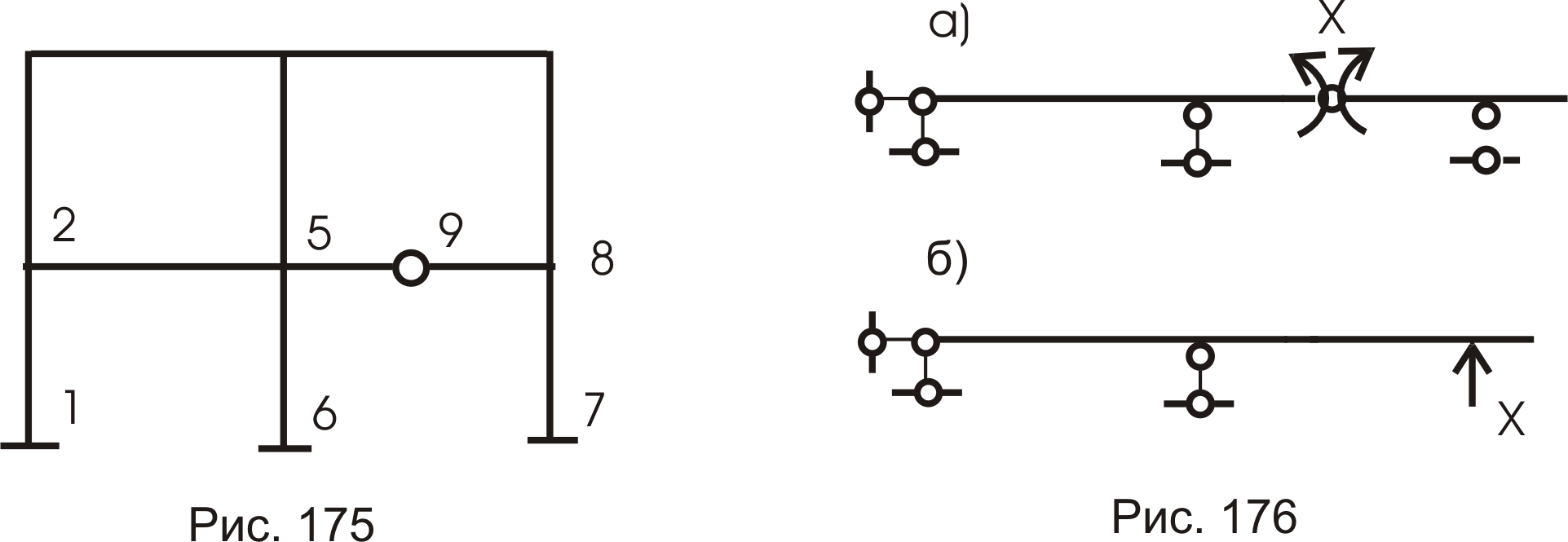
Уравнения совместности деформаций.

Как только основная система определилась, взамен отброшенных связей, прикладываются неизвестные усилия х₁, х₂,…х_i,…х_m (рис. 176).

Следует заметить:

1) Если отбрасывается внешняя связь (рис. 176б), то прикладывается одна сила х;

2) Если отбрасывается внутренняя связь (рис.177а,б), то прикладывается обобщенная двойная неизвестная сила, равная по величине и обратная по направлению.

Дальнейшие рассуждения проведем для конструкции, показанной на рис. 177б).

Усилия х_i и внешняя нагрузка вызывают перемещения точек приложения х_i по их направлению. Условие совместности деформации заключается в том, что взаимное перемещение от воздействия всех сил, действующих на конструкцию,

равно нулю. Используя принцип независимости действия сил, запишем для первого неизвестного х₁ (рис. г) данное условие:

где - перемещение точки приложения первой неизвестной по ее направлению, вызванному от действия первой неизвестной;

аналогично, перемещение точки приложения первой неизвестной по ее направлению, вызванному от действия второй, третьей неизвестных и внешней нагрузки, соответственно.

Положим , тогда можем записать в виде:

или условие (1) представится:

.

Аналогично запишется условие для перемещений точек приложения второй, третьей и т. д. неизвестных:

;

.

Полученные уравнения называются каноническими уравнениями метода сил. В этих уравнениях: - перемещение (обобщенные или независимые) точки приложения i-ой неизвестной по ее направлению от силы . Оно вычисляется по формуле Мора;

где - эпюры моментов от сил соответственно. Интеграл Мора вычисляется по правилам Верещагина или Симпсона, как это было рассмотрено ранее.

Решение системы канонических уравнений дает значение усилий , что позволяет рассчитать конструкцию обычным порядком.

Некоторые особенности и порядок расчета рассмотрим на примере.

Пример. Для заданной рамы (рис. 178) требуется построить M, Q, N.

1. Определяем степень статической неопределимости

Для получения основной системы нужно отбросить 2 избыточные связи.

2. Выбираем основную систему.

Варианты основной системы приведены на рисунке 179 а,б,в,г.

Для расчета возьмем вариант 2 (выбор произвольный).

3. Запишем канонические уравнения для решения:

;

.

Для подсчета коэффициентов и свободных членов уравнений построим эпюры от единичных сил и внешней нагрузки (рис. 180 а,б,в,г).

Вычисление основных параметров для построения эп. М от внешней нагрузки:

,

,

То же для построения М₁.

, ; .

И для построения М_2.

, .

4. Вычисляем коэффициенты при по правилу Верещагина:

,

,

.

Вычисляем грузовые слагаемые:

,

.

Перед решением системы уравнений производим проверку правильности вычислений коэффициентов:

а) построчная проверка

где - суммарная эпюра моментов от единичных сил (рис. 181) и для первой с троки

т. е. .

Равенство удовлетворяется.

б) суммарная проверка.

Сумма всех коэффициентов =

т.е. ;

т.е.

32,33=32,33.

Условие удовлетворяется.

в) проверка грузовых слагаемых

;

-8=-8.

Условие удовлетворяется.

5. Решение системы производим по методу Гаусса

Для этого разделим первое уравнение на 27, а второе – на 24. Получим:

Складываем оба уравнения:

Отсюда находим:

Подставляем х₂ в любое уравнение системы:

Вывод: Неизвестная реакция х₁ = - 1,21 направлена нами неправильно. Истинное направление реакции Н₄ будет вправо, а направление реакции Н₁ нами выбрано верно.

Дальнейший расчет может производиться двумя путями:

1) Приложив найденные усилия x_i к основной системе совместно с внешней нагрузкой (рис. 182), строим обычным способом эпюры М_ок, Q_ок, N_ок . Опорные реакции H₅, R₅, R₁ определяются из уравнений статики, и дальнейших пояснений не требуется.

Построение этим путем мы предоставляем читателю для самостоятельного решения.

2) Используем принцип независимости действия сил, а именно:

Поскольку эпюры перерезывающих и продольных сил обычно не строятся ни от единичных сил, ни от внешней нагрузки, то эпюра перерезывающих сил Q_ок строится по эпюре изгибающих моментов М_ок, а эпюра N_ок - по эпюре Q_ок.

Рассмотрим этот путь расчета. Для этого построим эпюры M_ix_i (рис. 183 а,б) и рядом - М_р. (рис. 183 в). Результат построения - эпюра М_ок (рис. 183 г).

Проверим правильность построения эпюры М_{ок .}

1. Статическая проверка.

Вырезаем узел 3 (рис. 184).

Составим уравнение статики

Условие удовлетворяется.

2. Кинематическая проверка.

Проверяем перемещение точки приложения силы x_i по ее направлению. Оно должно быть равно нулю, что отвечает условию совместности деформации

.

Перемножим М_ок на М₁

.

Ошибка составляет

.

Условие удовлетворяется.

По эпюре М_ок строим эпюру Q_ок. Для этого рассмотрим каждый стержень рамы, как отдельную балку, нагруженную системой сил: изгибающими моментами и

внешней нагрузкой (рис.185). Построив обычным путем эпюры Q для каждого участка, сформируем эпюру Q_ок (рис.186 а). Эпюра N_ок строится по эпюре Q_ок из условия равновесия узлов:

Вырезаем узел 4 (рис.187а) Вырезаем узел 3 (рис.187 б)

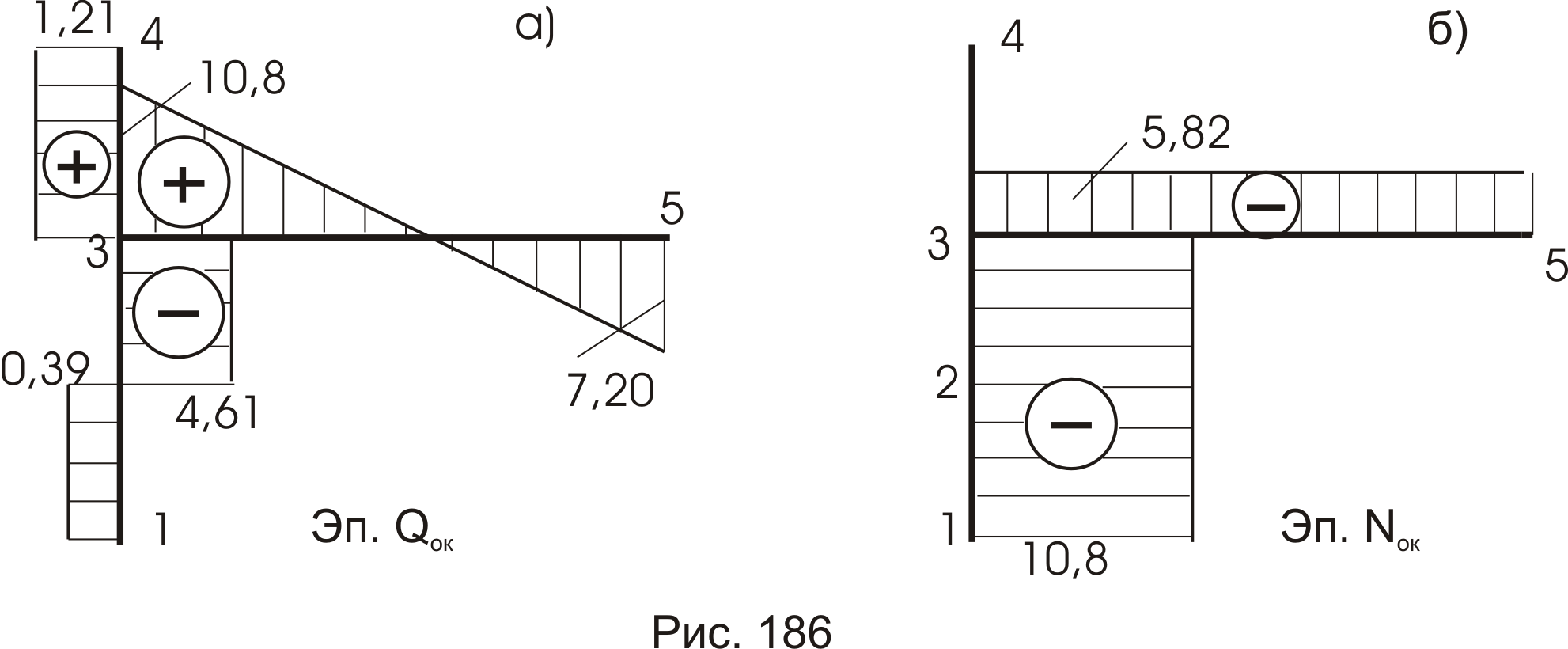
Эпюра N_ок показана на рисунке 186 б.

Многопролетные неразрезные балки

Методом сил довольно удачно производится расчет многопролетных неразрезных балок (рис. 188), которые используются в промышленном (подкрановые пути), да и в городском строительстве (эстакады, мостовые развязки и т. д.).

Примем некоторые правила:

- пролет балки (расстояние между соседними опорами, рис. 188) будем именовать по номеру правой опоры;

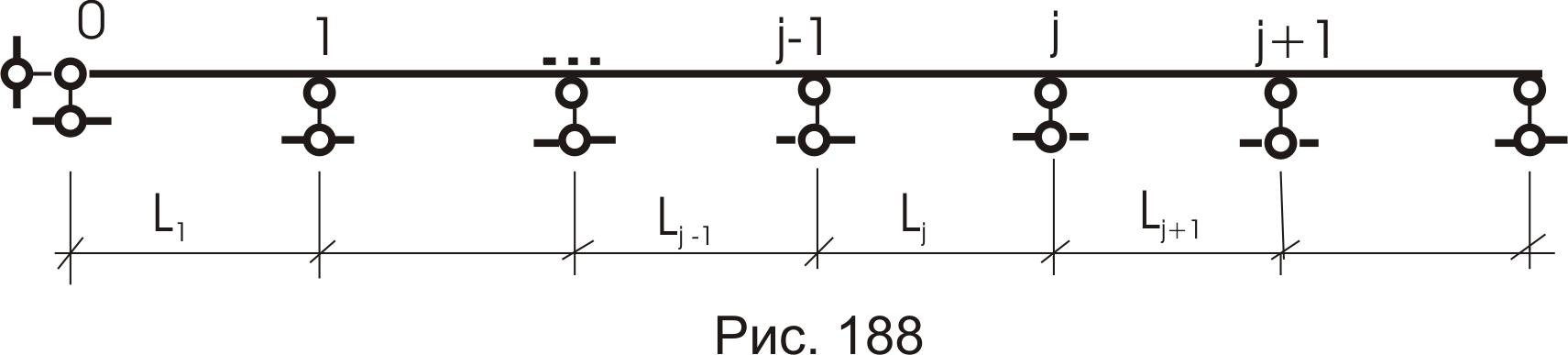
- нумерацию опор производим слева направо, начиная с нуля.

Степень статической неопределимости будем подсчитывать по упрощенному выражению

.

Основная система для неразрезной балки получается однозначно путем введения шарниров на опорах (рис. 189), что определяет в качестве неизвестных обобщенные изгибающие моменты на опорах. Направление их возьмем из предположения, что они растягивают нижние волокна. При такой основной системе единичные изгибающие моменты и не будут вызывать перемещений на опоре i (угол поворота на опоре i, рис. 189 а). Это позволяет упростить систему канонических уравнений:

………………………………………………………………………………

………………………………………………………………………………

Рассмотрим подробно одно общее уравнение системы, состоящее из 3-х моментов; скажем,для опоры i-ой

.

Вычислим значения коэффициентов перемножением эпюр (рис. 189 б,в,г ):

Грузовое слагаемое:

.

Из подобия треугольников ординаты y_i и y_i+1 определяются:

; .

Подставим значения ординат в выражение :

.

Нетрудно убедиться, что выражения и есть опорные реакции при загружении пролетов фиктивной нагрузкой по характеру и значениям, равным изгибающим моментам от внешней нагрузки в соответствующих пролетах, а именно (рис. 189 д).

Определим реакцию - го пролета (рис. 190 а):

;

;

.

Аналогично находим (рис. 190 б): .

Подставим все полученные значения в уравнение

.

Произведем преобразования:

- умножим уравнение на ;

- введем обозначение

проведенная длина i – го пролета , где J₀ – произвольный момент инерции.

Преобразования дают уравнение 3-х моментов в виде:

.

Рассмотрим пример (рис. 191).

В нашем примере неизвестные моменты М₀ и М₁. Момент на опоре 2 вычисляется (кн·м).

Записываем уравнения для М₀ и М₁:

1)

2)

здесь при EJ – const , тогда

1) , .

2) .

Определим фиктивные реакции.

Пролет 1 (рис. 191б).

.

.

; .

Пролет 2.

Учитывая симметричность загружения, можем обойтись без уравнения

статики (рис. 191 в).

Полученные значения подставим в уравнения и произведем преобразования:

или

.

Зная моменты на опорах, строим эпюру опорных моментов. Окончательная эпюра М_ок строится как результат сложения М_оп с М_пр (рис. 191 г). Момент на консоли строится обычным путем. Уже известным приемом по М_ок строится Q (рис. 191 д).

Говоря о расчете неразрезных балок, остановимся на частном загружении, а именно загружении балки только в одном пролете. В этом случае эпюра изгибающих моментов строится по моментно-фокусным отношениям.

Было подмечено, что при загружении одного пролета (рис. 192) значения

изгибающих моментов от загруженного пролета от опоры к опоре:

- затухают, становятся все меньщими;

- имеют переменные знаки, а значит имеется точка в пролете, в котором M = 0;

- с ростом нагрузки увеличиваются опорные моменты пропорционально, при этом точка, в которой M = 0, не меняет своего положения.

Последнее обстоятельство позволило записать:

и т. д.,

где k_i – коэффициент, который назван фокусным отношением. Различаются правые и левые фокусные отношения в зависимости от того, в какую сторону от загруженного пролета распространяются опорные моменты (в нашем примере правые фокусные отношения).

Для вычисления значения фокусных отношений рассмотрим i – ый пролет балки с нагрузкой, располагающейся где-то в пролете слева (рис. 193).

Запишем для M_i уравнение трех моментов:

.

Разделим уравнение на M_i

.

Как видно из рисунка,

; .

Из этих выражений мы можем записать:

; и

Значок «пр» у фокусного отношения означает, что вычисления ведем для правых фокусных отношений. Подставим полученные значения и в уравнение и получим:

.

Откуда и определим :

.

Приведя подобные, получим:

.

Аналогично произведя преобразования, получим выражение для левых фокусных отношений (рис. 194):

Как видно из полученных выражений, вычисления фокусных отношений приведут нас к началу (левые фокусные отношения) или к концу балки (правые фокусные отношения).

Начальное или конечное опирания могут быть: шарнирным опиранием или заделкой.

Шарнирное опирание (рис.195)

, ,

, .

Заделка (рис.196 а).

Заделку можем представить с нулевым пролетом (рис. 196 б), тогда

,

где , тогда .

Выводы:

1. Ближайшее фокусное отношение у шарнирной опоры равно бесконечности.

2. Ближайшее фокусное отношение у опоры – заделки равно 2.

Пример (рис. 197)

Значения моментов на первой и второй опорах найдем, записав для них уравнения трех моментов:

где ; ; ; .

Нужно определить фокусные отношения:

а) левые

б) правые

.

Подставим эти выражения в систему уравнений

;

,

Приведя подобные и решив систему уравнений, получим :

Тогда

.

Эпюра моментов показана на рисунке 197.

4. Метод перемещений

1. Основные понятия.

Выделим для рассуждений из конструкции отдельный элемент в виде прямолинейного стержня. От воздействия внешней нагрузки стержень займет новое положение – деформированное (рис. 198).

Разберем перемещение стержня поэтапно:

1. Стержень поступательно переместится из положения А – В в положение А₁ – В₁ по горизонтали - _гор. и по вертикали -_верт..

2. Стержень повернется на угол  - положение (рис.198, тонкие линии).

Напомним, что данные перемещения не вызывают внутренних усилий в стержне.

3. Перемещение точки в положение по отношению к точке вызывает искривление стержня, а значит и внутренние усилия.

4. Сечение и сечение при воздействии нагрузки поворачиваются на углы и , что вызывает деформацию стержня и вместе с этим- внутренние усилия в стержне.

Следовательно, за неизвестные перемещения принимаем относительные линейные смещения и угловые перемещения концов стержня, т. е. общее число неизвестных конструкций вычисляется по выражению

.

Подсчет угловых перемещений - .

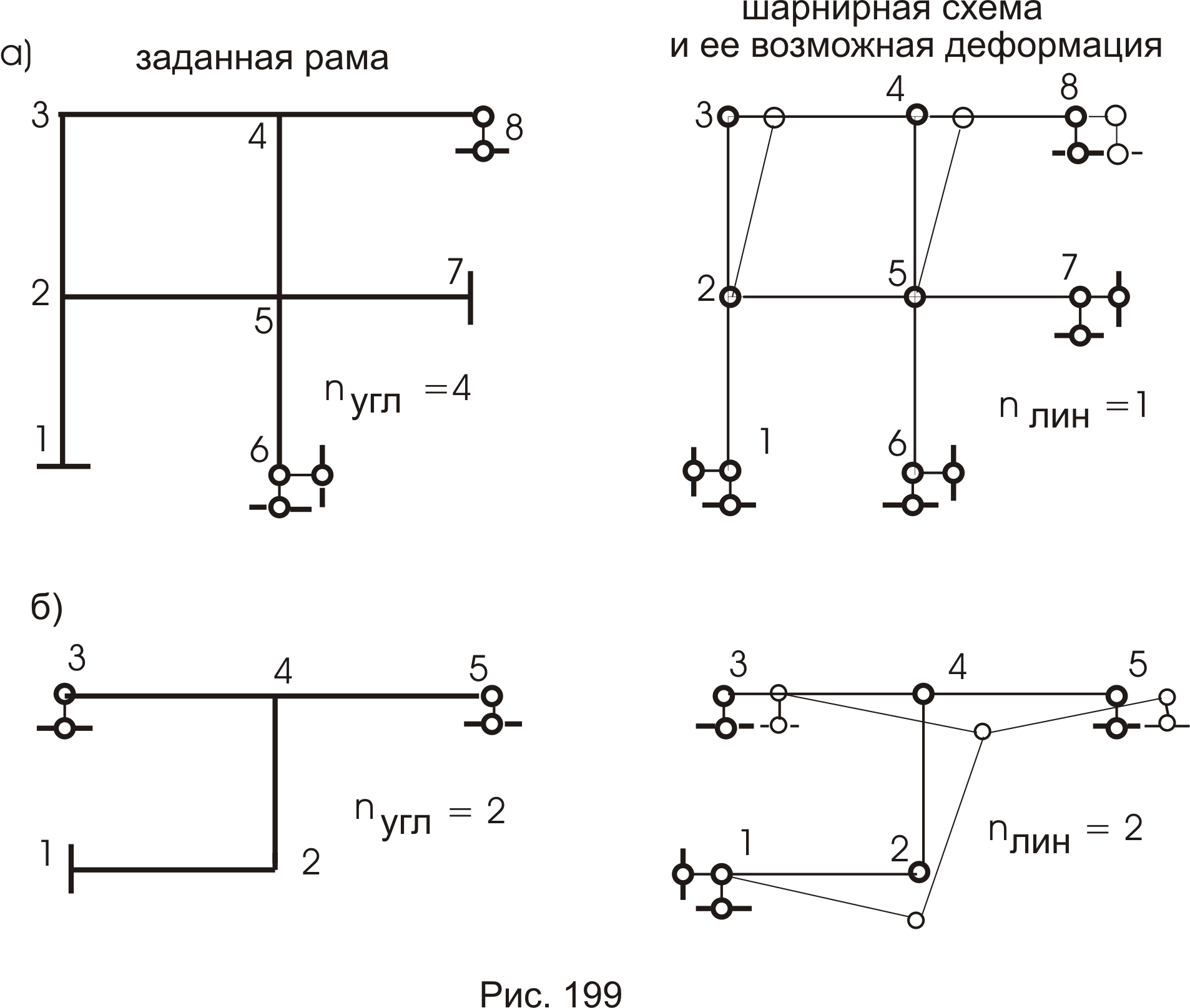
Стержни в конструкции соединяются между собой шарнирно, либо жестко. В шарнирном соединении сечения стержни поворачиваются свободно и не вызывают внутренних усилий. В жестком узле концы стержней с учетом совместности их деформаций поворачиваются на один угол. Следовательно, подсчет сводится к простому пересчету жестких узлов конструкции (рис.199).

Подсчет линейных перемещений -

Относительное перемещение узлов численно равно степени свободы шарнирной схемы заданной конструкции, т. е. во все жесткие узлы, включая и опорные заделки, вводим полные шарниры (рис. 199 a,б).

Итак, для рамы (рис. 199 а) имеем 4 жестких узла (2, 3, 4, 5), что дает

Шарнирная схема дает

Одно линейное смещение и возможная при этом деформация рамы приведены на схеме (рис. 199а). Для рамы (рис. 199б) имеем 2 жестких узла (2, 4), что определяет , а шарнирная схема дает две степени свободы, что определяет

Нужно отметить, что если и система полностью или ее участок мгновенно-изменяем, что требует постановки связи, то будет равно количеству линейных связей, устанавливаемых в шарнирную схему конструкции для обеспечения ее неизменяемости и неподвижности (рис. 200).

2. Основная система (расчетная модель).

получается наложением связей на возможные перемещения:

- в жесткие узлы вводим заделку, препятствующую только повороту узла, но не препятствующую линейному перемещению;

- линейные связи (опорные стержни) устанавливаем в узлы по направлению возможных перемещений шарнирной схемы конструкции.

Основные системы для рам (рис. 199) показаны на рисунке 201. Нумерация связей обозначена в кружочках.