7. Теорема о взаимности перемещений

Из выражения нетрудно видеть, что при Р₁ = Р₂ = 1

.

В дальнейшем перемещения от единичных сил будем обозначать строчной буквой дельта - .

Тогда получаем или - Теорема Максвелла.

Перемещение точки приложения первой единичной силы по ее направлению, вызванное второй единичной силой, равно перемещению точки приложения второй единичной силы по ее направлению, вызванному первой единичной силой.

8. Определение перемещений

Рассмотрим конструкцию (балку), загруженную двумя системами сил:

1. произвольной внешней нагрузкой (грузовое состояние);

2. единичной силой (единичное состояние).

Внешняя нагрузка вызывает:

а) перемещение точки А приложения единичной силы по ее направлению - ;

б) внутренние деформации - .

Единичная сила вызовет внутренние усилия .

Составим возможную работу сил единичного состояния на перемещениях грузового состояния (внешнюю работу и внутреннюю работу).

Данная формула носит название «формула Мора»

Для конструкций, в основном подверженных изгибу (балки, рамы), в формуле учитывается только слагаемое с М, т. е.

.

Влияние Q и N мало ( 3%).

Для конструкций, в основном работающих на продольные усилия (фермы), в формуле учитывается слагаемое с N, т .е.

.

Для арок учитываются все слагаемые.

Порядок определения перемещений

1. Приложить единичную силу в точку, перемещения которой определяются по требуемому направлению;

2. Построить эпюры внутренних усилий от единичной нагрузки;

3. Построить эпюры внутренних усилий от внешней нагрузки;

4. Подсчитать перемещение по формуле Мора.

На рисунке 155 приведены варианты приложения единичной нагрузки в зависимости от требуемой задачи: горизонтальное перемещение точки; угол поворота сечения; взаимное сближение или удаление точек; взаимный угол поворота сечений.

Пример.

Требуется:

1. Определить перемещение точки «К» в середине пролета (рис. 156а).

Решение.

Приложим силу Р = 1 в точку «К» направлением вниз, совпадающим с возможным перемещением точки «К» (рис. 156 б).

2. Построим эпюру М от грузового состояния с .

3. Построим эпюру М от единичного состояния с .

3. Подставляем значения моментов в выражение перемещения:

= .

Вычисление интегралов формулы Мора (формулы перемещений) производится по правилу Верещагина и по правилу Симпсона.

Правило Верещагина:

где : - площадь эпюры моментов грузового состояния;

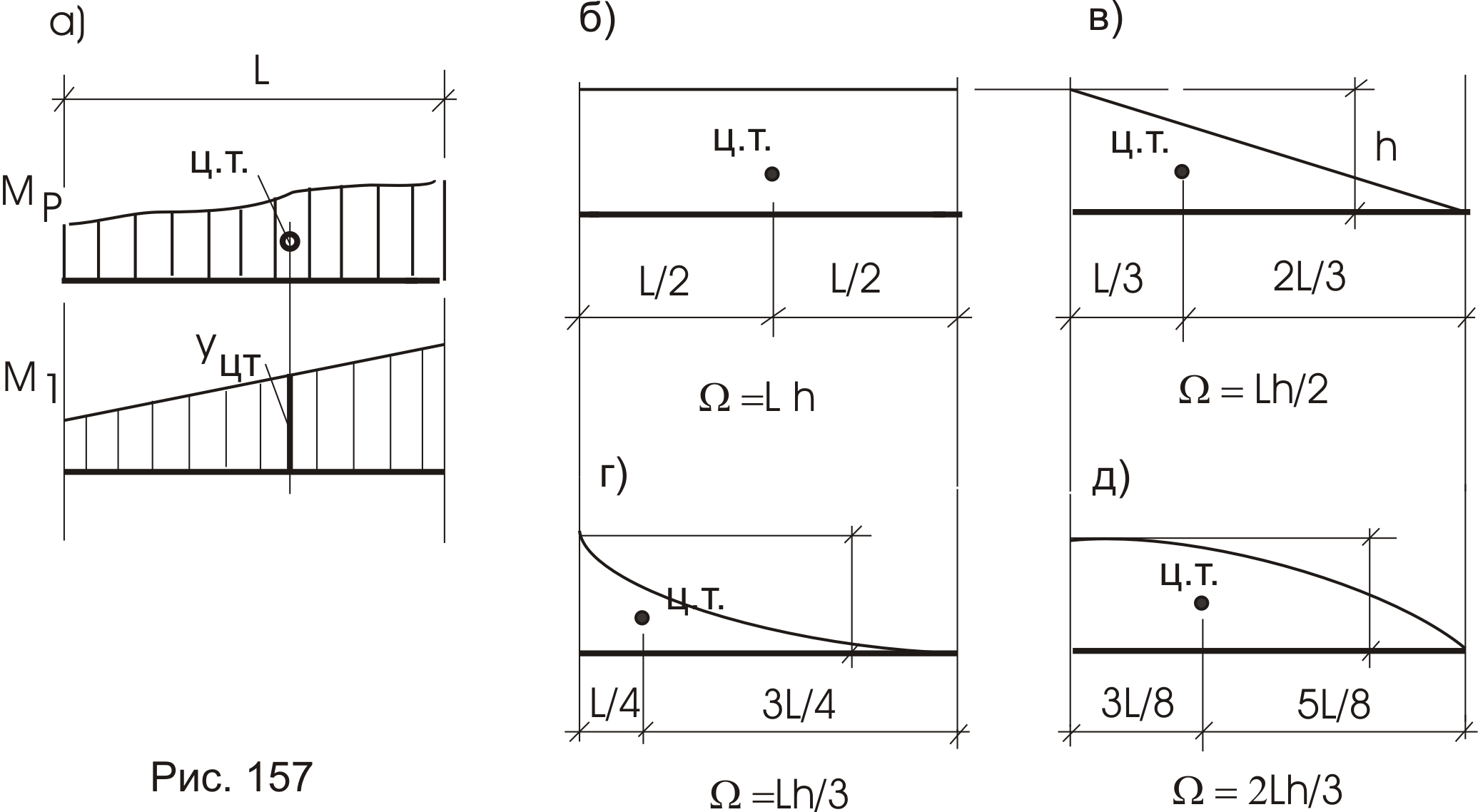
ордината, взятая из эпюры единичного состояния под центром тяжести эпюры изгибающих моментов грузового состояния (рис. 157а).

Приведем некоторые значения положений центров тяжести простых фигур – М_р. (рис. 157 б,в,г,д).

Варианты перемножения эпюр (рис. 158):

а) перемножение трапеции с треугольником (рис. 158а):

.

б) Перемножение переменной трапеции с трапецией (рис. 158б):

.

в) Перемножение квадратной параболы общего положения с трапецией (рис. 158 в):

.

Правило знаков: перемещение положительное, если значения обоих изгибающих моментов откладываются по одну сторону от оси стержня.

Правило Симпсона:

,

где: М_р^н, М_р^с, М_р^к – значения изгибающего момента от внешней нагрузки в начале, середине и в конце элемента (стержня) конструкции, соответственно;

М₁^н, М₁^с, М₁^к - значения изгибающего момента от единичной нагрузки в начале, середине и в конце этого же элемента (рис. 159);

L_j – длина элемента конструкции;

ЕJ – жесткость элемента на изгиб.

9. Примеры определения перемещений в упругих системах