5. Расчет конструкций и их элементов

1. Вводная часть

Под расчетом сооружения понимается определение внутренних усилий во всех элементах сооружения и их деформаций.

Внутренние усилия – усилия, возникающие в элементах сооружения вследствие их деформации от воздействия на сооружение внешней нагрузки.

Под деформацией элементов конструкции и конструкции в целом понимается изменение размеров конструкции и ее формы.

Знакомство с методами расчета, видами деформаций начнем с простых элементов сооружения – балки, стержня.

В основу расчета положен метод сечений.

Рассмотрим балку произвольной формы поперечного сечения, нагруженную произвольной системой сил (рис. 75). Рассечем ее плоскостью, перпендикулярной к оси балки. В результате этого сечения балка разделится на две части: левую, с приложенными к ней силами Р₁, Р₂, Р₆ , и правую, с приложенными к ней силами Р₃, Р₄, Р₅.

Использование секущей плоскости и определяет метод сечения.

Далее рассмотрим одну из полученных частей балки (левую) (рис. 75). При дальнейшем рассуждении мы будем иметь в виду:

• тело бруса (иного элемента) идеально упругое;

• сплошное (без изъянов);

• однородное и изотропное, т. е. во всех его точках и во всех направлениях упругие свойства одинаковы.

В месте сечения по площади поперечного сечения, как результат взаимодействия правой части на левую (левой на правую), возникнут внутренние усилия, которые в общем случае можно представить в виде (рис.76):

а) продольное усилие – N_x (оно направлено вдоль оси элемента конструкции);

б) перерезывающее усилие (сила) Q_y (оно направлено вдоль оси y );

в) перерезывающая сила Q_z (она направлена вдоль оси z);

г) момент относительно оси x;

д) момент относительно оси y;

е) момент относительно оси z.

Всего имеем шесть составляющих внутренних усилий.

Используя принцип независимости действия сил, можем общее воздействие сил на элемент конструкции рассмотреть как отдельные простые виды воздействия и им присущие виды деформации:

а) продольное усилие, деформации растяжения или сжатия;

б) сдвигающие усилия, деформации сдвига (среза);

в) крутящие усилия, деформации кручения (сдвига);

г) изгибающие усилия, деформации изгиба.

Для плоской задачи (рис. 77) количество внутренних усилий сокращается до трех:

а) продольное усилие –N_x ;

б) перерезывающая сила – Q_y;

в) момент относительно оси z (относительно точки), который вызывает изгиб элемента конструкции и носит название изгибающий момент.

Следует помнить: если брус до сечения находится в равновесии, то и после сечения обе его части (рис. 77б) находятся в равновесии. Следовательно, для левой рассматриваемой части справедливы уравнения статического равновесия:

1. 2. 3. .

По характеру приложения нагрузки получаем и соответствующие им внутренние усилия, следовательно и деформации: растяжение (сжатие), сдвиг, изгиб, кручение и их комбинации.

2. Растяжение, сжатие прямого бруса (стержня)

Рассмотрим стержень (брус), нагруженный растягивающими силами, линии действия которых совпадают с осью стержня (рис. 78а). Рассечем стержень плоскостью (сечение 1 – 1) и рассмотрим левую часть стержня (рис. 78б).

На рассматриваемую часть бруса действуют силы: Р – внешняя нагрузка, приложенная к левому концу бруса; dP – элементарное внутреннее усилие, приложенное (действующее) к элементарной площади dF сечения (рис. 78в).

Рис. 78

Составим уравнения равновесия: спроецируем все силы, действующие на левую часть бруса, на ось х:

.

Отсюда:

.

Интеграл левой части уравнения представляет собой равнодействующую силу N_(x) в сечении х.

Приняв, что dP по площади сечения распределяется равномерно, можем записать:

. Интеграл дает величину площади сечения – F_(x) , тогда

или

.

Обозначим dP = ,

где  - нормальное напряжение во всех точках поперечного сечения при растяжении (сжатии), т. е.

.

Следовательно, первоначально мы должны определить внутреннюю продольную силу N по длине бруса, т. е. построить график ее изменения по длине стержня (бруса). Этот график называем – эпюра. Для стержня, загруженного двумя силами Р (рис. 79а), проведем сечение 1 – 1 в произвольном сечении х.

Как и ранее, рассмотрим левую часть стержня ; ; .

Из уравнения видим, что усилие по длине стержня не зависит от ординаты х – поэтому ее величина по длине стержня постоянная и равна Р (рис. 79в).

Примем:

продольное усилие положительное, т. е. растягивающее, если оно направлено от сечения (рис. 80), и отрицательное, если оно направлено к сечению, т. е. происходит сжатие.

Рассмотрим ряд примеров.

Пример 1. Стержень переменного сечения по длине загружен тремя силами (рис. 81).

Проведем в произвольном месте в промежутке от точки А до точки В сечение 1 – 1.

Рассмотрим нижнюю часть стержня (рис. 82а). Составим уравнение равновесия: ; ; .

От точки А до точки В усилие продольное N = 10 kн. (растягивающее – см. рис. 83б).

Проведем сечение 2 – 2 на участке стержня (рис. 82б). Уравнение равновесия примет вид:

; ; (усилие растягивающее).

Рис 82

Эпюра N на этом участке показана на рис. 83б.

Проведем на участке от точки С до точки D (заделки) в произвольном месте сечение 3 – 3. И вновь рассмотрим равновесие нижней части (рис. 82в):

; ; .

Эпюру N на этом участке см. рис. 83б).

Из анализа эпюры N можно сделать выводы:

а) на участке между двумя сосредоточенными силами продольное усилие постоянное и не зависит от площади поперечного сечения стержня;

б) в точке приложения сосредоточенной продольной силы на эпюре внутреннего усилия N наблюдается скачок на величину этой силы.

Эпюра напряжений (рис. 83в) строится по величине напряжений, вычисляемых из выражения:

.

На первом участке (от точки А до точки В)

.

На втором участке (от точки В до точки С) нужно учесть, что площадь поперечного сечения стержня меняется:

для F = 10 см²:

;

для F = 20 см²:

.

На этом участке на эпюре нормальных напряжений в месте изменения площади поперечного сечения наблюдается скачок (рис. 83в).

На третьем участке нормальное напряжение

.

Пример 2. Стержень загружен равномерно распределенной нагрузкой от собственного веса (рис. 84а).

Построим эпюру N.

Рассечем на расстоянии y стержень плоскостью 1 – 1 и рассмотрим нижнюю часть (рис. 84б). Запишем уравнения равновесия

; ; .

Продольная сила меняется по линейному закону при z = 0 ; N=0, при z = 6

N = 36 = 18 (кн). Эпюра продольных усилий представлена на рис. 84в.

2. Растяжение (сжатие) прямого стержня.

Вернемся к стержню, нагруженному растягивающими силами (рис. 85). Для дальнейших рассуждений будем считать, что левый его конец неподвижен (заделан). Под действием силы Р стержень удлинится – его длина станет размером L₁. Вычислим величину удлинения, для чего возьмем разницу конечной длины и первоначальной, т. е.

.

Приращение длины стержня назовем абсолютным удлинением при растяжении. При этом будем считать, что:

• все плоские сечения до и после деформации остаются плоскими;

• величина площади поперечного сечения не меняется при деформации.

Возьмем отношение приращения - L к первоначальной длине стержня – L и назовем его относительное удлинение -  (эпсилон):

(величина безразмерная).

Обратимся к опытным данным различных образцов из различных материалов при растяжении. Установлено, что на графике (рис. 86), на котором напряжения и деформации откладывались на взаимно перпендикулярных осях,

с ростом напряжений, которые растут с ростом нагрузки, прямо пропорционально растут и относительные деформации стержня до какой-то точки А. После этой точки линейный закон нарушается. Точка А соответствует пределу пропорциональности. Нас будет интересовать та часть графика, которая относится к упругой стадии растяжения (сжатия).

О пустим перпендикуляр из точки А на ось  - точку В. Возьмем отношение

.

АВ будет соответствовать . ВО будет соответствовать  . Перепишем это соотношение в виде:

или .

Здесь tg  выступает как коэффициент пропорциональности.

Вывод: для упругих систем деформация прямо пропорциональна напряжению (нагрузке). Этот вывод сделан в 1678 году Робертом Гуком и известен как закон Гука. Этот закон является одним из основных законов при расчете конструкций.

Установим, что же кроется под величиной tg . Отрезок ОА на графике (рис. 86) для различных материалов имеет различный угол наклона - . Он целиком зависит от физических свойств материала (металл, бетон, дерево и т. д.), которые характеризуются модулем упругости (модулем Юнга, по имени ученого, который ввел этот параметр материалов) и обозначается буквой Е. Тогда наша зависимость примет вид:

Е имеет размерность ед. силы / ед. площади.

Эту зависимость перепишем:

Но .

Подставим эти значения в выражение и получим:

или

здесь EF – жесткость стержня (бруса) при растяжении (сжатии).

Вывод:

Удлинение (укорочение) стержня прямо пропорционально нагрузке и его длине и обратно пропорционально жесткости стержня при растяжении (сжатии).

В заключение отметим, что модули деформации Е для различных материалов приведены в справочной литературе.

3.Расчет ферм

Ферма относится к такому типу сооружений, у которого, учитывая принятую расчетную схему, в стержнях, образующих структуру фермы, возникают только продольные усилия. (Напомним особенности расчетной схемы фермы: соединение стержней в узлах - шарнирное, причем, оси стержней, входящих в узел пересекаются в оси шарнира; нагрузка прикладывается только в узлах в виде сосредоточенных сил – рис. 87 ).

В расчете фермы используется опять-таки метод сечений. В зависимости от характера проведения сечения различают два способа:

а) способ вырезания узлов; б) способ сквозного сечения.

а) Способ вырезания узлов

Рассмотрим для примера балочную ферму с параллельными поясами (рис. 87).

Пронумеруем узлы фермы цифрами (порядок нумерации произвольный).

Шарнирное соединение стержней в узлах создает сходящиеся системы сил. Следовательно, вырезая узел (разрезая стержни, входящие в узел, круговым сечением), можем рассматривать его равновесие отдельно. Поскольку для сходящейся системы сил для плоской задачи имеем только два уравнения равновесия, то вначале мы можем вырезать узел только с двумя неизвестными усилиями. Анализ данной фермы показывает, что таких узлов нет. Но!

Рассмотрим равновесие всей фермы в целом. От воздействия внешней нагрузки в опорных устройствах по направлению опорных стержней возникают три опорные реакции. Для их определения имеются три уравнения равновесия:

1. ; 2. ; 3. .

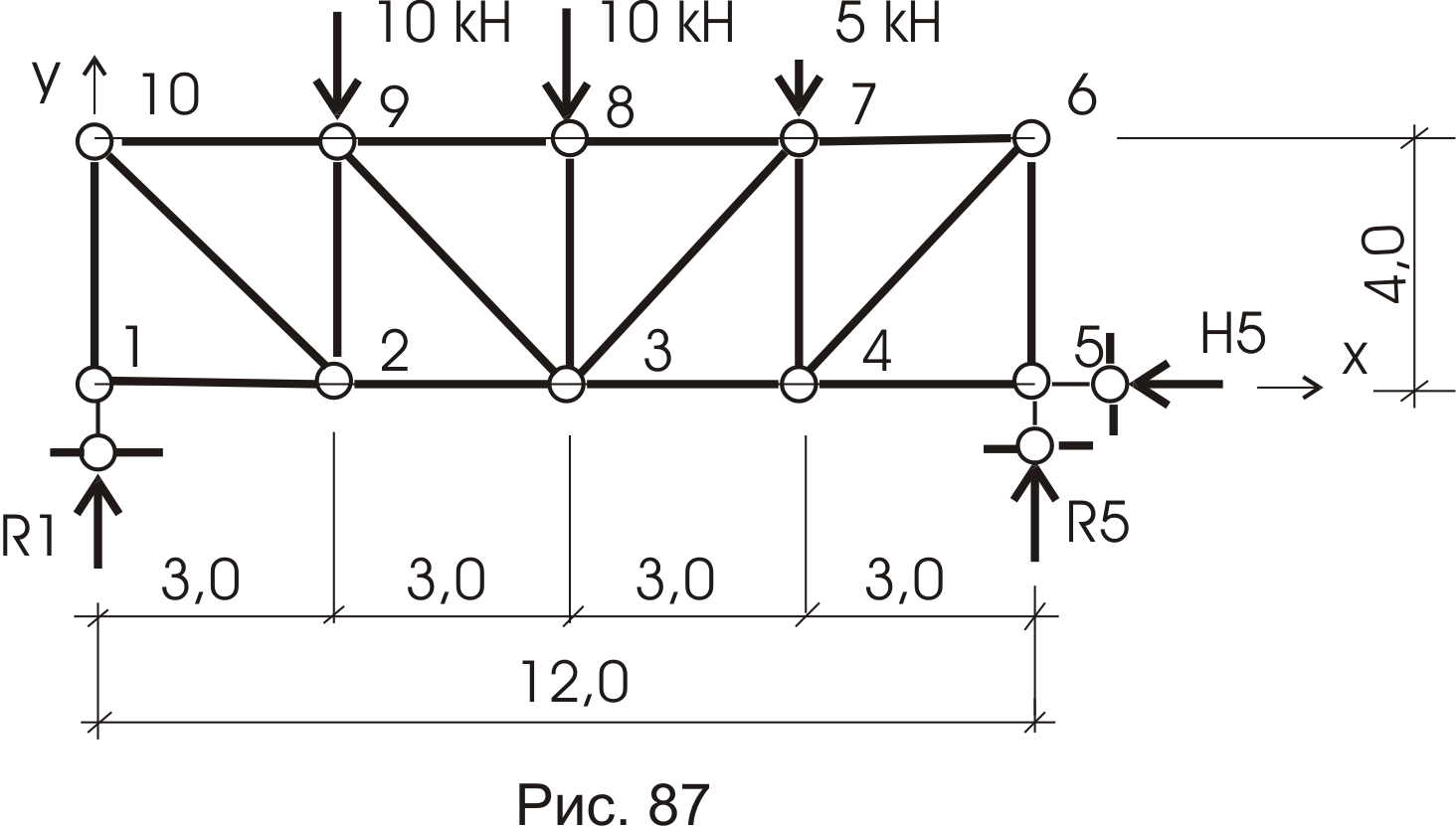
Направим произвольно реактивные усилия по направлению опорных стержней. Составим отмеченные уравнения последовательно:

1. ;

2. ;

3. .

Из третьего уравнения R₅ = 11,25 (кн). Из второго уравнения R₁ = 13,75 (кн).

В этом случае реактивные усилия выступают как внешняя нагрузка и мы можем воспользоваться вырезанием узла 1 или 5 (рис. 88а). Усилия в стержнях фермы будем обозначать с индексами, числа которых совпадают с номерами узлов, соединяющихся этим стержнем.

Система сходящихся сил находится в равновесии. Для этой системы запишем:

;

; .

Из решения можем сделать важный вывод:

а) если в узел сходятся три стержня (усилия), два из которых лежат на одной прямой (узел 1 – усилие R₁ и N_1·10 в стержне 1-10), и узел не загружен, то усилие в отдельно стоящем (третьем) стержне равно нулю, т.е. N_1-2 = 0.

б) если в узел (узел 5) сходятся четыре усилия (стержня), два из которых попарно лежат на одной прямой, то усилия в этих стержнях (лежащих на одной прямой) равны между собой по величине и по знаку (N_5-6 = - R₅ и N_4-5 = - H₅).

На основании этих частных случаев (выводов) можно точно сказать, что в стержне 4-5 усилие N_4-5 = 0, а в стержне 5-6 усилие .

Следующим можем вырезать только узел 10 (рис.88б) или узел 6. Воспользуемся уравнениями равновесия:

1. ; .

Cos α или Sin α вычисляются из геометрии фермы.

2. ; .

Из второго уравнения: .

Подставим значение , и получим: .

Из первого уравнения определяем

Последующий вырезается узел 2 (или узел 4), затем узел 9 (или узел 7).

Узел 8 относится к частному случаю:

а .

б) Способ сквозного сечения

Для нахождения усилий в стержнях, скажем, второй панели: , проведем сечение 1 – 1, рассекая нашу ферму по этим стержням (рис. 87). Рассмотрим далее одну из частей фермы (правую или левую) (рис. 89). Рассматриваемая часть находится в равновесии и для нее справедливы уравнения статики:

1. ;

2. ;

3. .

Определяем усилие .

Необходимо использовать одно из уравнений статики, чтобы искомое усилие определилось из этого уравнения. Усилия и сходятся в точке (узле) 3. Запишем уравнение моментов относительно узла (точки) 3 всех сил, действующих на левую часть фермы:

; .

Из этого уравнения :

.

Определяем усилие .

Запишем уравнение равновесия:

; .

.

Для определения усилия используем уравнение – сумма проекций на ось y:

; .

.

Вывод:

Сечение проводится по трем стержням с неизвестными усилиями, т. к. для их определения можем использовать только три уравнения статического равновесия.

4. Деформация сдвига

Понятия о сдвиге.

Сдвиг – это деформация стержня (бруса) от воздействия двух перпендикулярно направленных к оси стержня сил разного направления (рис. 90), приложенных практически в одну точку – А. Происходит срез подобно тому, как мы разрезаем ножницами бумагу или лист железа.

Если две силы, которые называются перерезывающими (поперечными), отодвинуть на некоторое малое расстояние друг от друга, то в начальный момент будем наблюдать перекашивание прямых углов параллелепипеда (рис. 91). Выделим этот элемент двумя плоскостями и рассмотрим его деформации (рис. 92а).

Напряжения и деформации при сдвиге.

Левый конец элемента будем считать неподвижным (защемим его). Под действием силы Р правый его конец переместится. При этом будем считать: плоское сечение в результате деформации остается плоским. Введем обозначения: Δ – перемещение точки. В (С) назовем абсолютным сдвигом. Он зависит от величины силы Р и длины dx стержня (бруса). Отношение абсолютного сдвига (Δ) к длине dx стержня (бруса) называется относительным сдвигом и выражается в радианах, т. е. углом сдвига:

,

ввиду малых деформаций tgγ = γ, тогда

.

При выделении из стержня элемента dx в его плоскостях (плоскости ВС, допустим) возникают внутренние силы, которые направлены вдоль плоскости среза, и которые называются перерезывающимися силами – Q. Если эту силу разделить на площадь сечения – F, то получим касательные напряжения - , т. е. .

Будем считать, что касательные напряжения равномерно распределяются по площади сечения (рис. 92б).

Между напряжениями ( ) и относительными деформациями при сдвиге (γ) действует закон Гука, т. е. напряжения прямо пропорциональны деформациям:

,

где G – модуль упругости материала при сдвиге.

Запишем : , но ; , тогда

или .

Экспериментами установлено, что модули упругости при растяжении (сжатии) и при сдвиге связаны соотношениями:

Пример. Рассчитать соединение врубки стропила с нижним поясом стропильной фермы (рис. 93а). Материал – дерево (сосна).

; .

Решение.

1. Подсчитаем площадь сжатия от нагрузки N = 500 кн:

; .

Примем глубину врезки h = 2,5 см.

Вычислим величину (рис. 93б):

.

Отсюда:

.

Принимаем а = 22 см.

5. Плоский изгиб

Плоский изгиб – вид деформации балки (конструкции) от воздействия на нее нагрузки, расположенной в плоскости одной из главных осей сечения. Причем, деформация балки происходит в этой же плоскости.

Наша задача:

Определить внутренние усилия (изгибающий момент, перерезывающую силу, продольное усилие) в любом сечении по длине балки.

Определить закон изменения внутренних усилий по высоте сечения балки.

Определить деформацию балки, т.е. определить в любом сечении балки ее прогиб и угол поворота сечения.

1. Внутренние усилия по оси балки.

Рассмотрим балку, опирающуюся на две опоры (рис. 94) и нагруженную одной сосредоточенной силой Р. Расстояние между опорами обозначим через L. Для определения опорных реакций А, В, Н (рис. 94) используем три уравнения статического равновесия:

1. ; Н = 0,

2. ; А – Р + В = 0, А + В = Р,

3. ; - В L + Р а = 0, .

Опорная реакция А найдется из уравнения 2, а можно еще раз составить уравнение 3, но момент взять относительно точки В:

3. ; А L – P b = 0; .

Итак, мы имеем балку, нагруженную уравновешенной системой сил. Определим внутренние усилия в балке.

Возьмем произвольное сечение х балки и рассмотрим равновесие ее левой (или правой) части (рис. 95). В сечении х возникнут усилия М, Q, N, т.е. изгибающий момент, перерезывающая сила и продольное усилие, как воздействие отброшенной правой (левой) части. Для определения их величин составим уравнения равновесия рассматриваемой левой части балки:

; ,

из этого уравнения находим .

Правило: изгибающий момент откладывается со стороны растянутых волокон.

; ,

отсюда определяем .

Правило: перерезывающая сила положительная, если ее направление относительно сечения создает момент по часовой стрелке (рис. 96).

; ,

откуда .

Правило знаков для продольного усилия было отмечено ранее.

Закон изменения внутренних усилий по длине балки лучше (нагляднее) виден из их графиков (эпюр), построенных под балкой по ее оси.

Перейдем к построению эпюры М.

Для построения балку разобьем на участки:

Участок 1: А-С (от опоры А до точки приложения силы, рис. 97а).

Выражение изгибающего момента на этом участке запишется (от левых сил):

при х = 0 значение момента ,

при х = а или, подставляя ,

получим: .

Участок 2: С-В (от точки приложения силы до опоры В, рис. 97а).

Изгибающий момент запишется от сил левой части:

,

при х = а или ,

при х = L .

Значения изгибающих моментов согласно правилу откладываем со стороны растянутых волокон (рис. 97б).

Эпюра перерезывающих сил.

Участок 1: А-С. От опоры А до точки С, причем сечение в точке приложения силы берем бесконечно близко слева от силы.

,

заметим, что величина перерезывающей силы на этом участке не зависит от места положения сечения, т.е. величина - постоянная и положительная.

Участок 2: С-В. От точки С бесконечно близко справа до опоры В:

,

На этом участке величина постоянная (рис. 97в). Отметим, что в месте приложения сосредоточенной силы Р на эпюре наблюдаем скачок на величину силы Р.

Рассмотрим балку, нагруженную равномерно распределенной нагрузкой по всей длине балки (рис. 98).

1. Определение опорных реакций.

; Н = 0,

; ,

; ,

из этого уравнения находим величину реакции В:

.

Из второго уравнения определим реакцию опоры А:

.

2. Построение эпюр внутренних усилий (M_(x) и Q_(x)).

Балка имеет один участок от опоры А до опоры В.

Изгибающий момент (рис. 98б):

.

Из выражения изгибающего момента видим, что изгибающий момент по длине балки меняется по квадратной параболе с максимальным значением в середине балки:

х=0 М_(х) = 0.

.

х = L М_(х) = 0.

Перерезывающая сила (рис. 98в).

.

Из выражения перерезывающей силы следует, что ее значение меняется по линейному закону. Для построения эпюры достаточно подсчитать значение Q_(x) при:

x= 0 ,

x=L .

Из анализа приведенных примеров можем сформулировать основные правила изменения величин перерезывающей силы и изгибающего момента по длине конструкции, а также их взаимозависимость, которые помогут проконтролировать правильность построения эпюр.

Для перерезывающей силы:

1) на участке конструкции (балки), свободной от нагрузки, перерезывающая сила - величина постоянная;

2) на участке балки, загруженном равномерно распределенной нагрузкой, перерезывающая сила меняется по линейному закону вида qх;

3) в точке приложения сосредоточенной нагрузки (в том числе и опорной реакции) на эпюре перерезывающей силы наблюдается скачок на величину этой силы.

Для изгибающего момента:

1) изгибающий момент в шарнире, соединяющем два и более дисков, равен нулю. Изгибающий момент равен нулю и на шарнирной опоре (подвижной и неподвижной), если шарнирная опора находится на концах балки (рис. 97);

2) на участке конструкции, свободном от нагрузки, изгибающий момент изменяется по линейному закону вида аx;

3) на участке конструкции, загруженном равномерно распределенной нагрузкой, изгибающий момент меняется по квадратной параболе, причем фокус параболы обращен навстречу действию нагрузки (рис. 98);

4) в точке приложения сосредоточенной силы график изгибающего момента в имеет перелом (рис. 97-точка С);

5) в точке приложения сосредоточенного изгибающего момента на эпюре изгибающего момента в этой точке наблюдается скачок на величину этого момента (рис. 99 – приведенный пример рекомендуется решить самостоятельно и результаты сравнить).

Связь между эпюрой перерезывающей силы и эпюрой изгибающего момента:

1) на участке, где перерезывающая сила постоянная, изгибающий момент меняется по линейному закону вида ах;

2) на участке, где перерезывающая сила равна нулю, изгибающий момент -величина постоянная (рис. 100);

3) на участке , где перерезывающая сила меняется по линейному закону, изгибающий момент меняется по квадратной параболе (рис. 98), причем в точке, где перерезывающая сила равна нулю, изгибающий момент имеет экстремальное значение.

Для нахождения положения этой точки выражение перерезывающей силы на этом участке приравниваем нулю, т.е.

.

Из этого выражения находим . Полученное значение подставляем в выражение изгибающего момента на данном участке:

.

2. Закон изменения внутренних усилий по высоте сечения балки.

Геометрическая сторона задачи.

На боковую поверхность балки нанесем сетку с прямоугольными ячейками, как показано на рис. 101а. Загрузим балку. В результате деформации балки сетка изменит свое очертание: горизонтальные линии искривляются, причем нижние линии растягиваются по отношению к первоначальным, а верхние укорачиваются. И только одна линия остается равной первоначальной – назовем ее нейтральной линией (Н.Л.) (рис. 101б). Вертикальные линии сетки, поворачиваясь, остаются прямыми и сохраняют практически прямой угол к изогнутым линиям. Эту особенность деформации при плоском изгибе впервые отметил Яков Бернулли (1705 г.), и до нас она дошла как гипотеза плоских сечений или гипотеза Бернулли.

Вырежем двумя плоскими сечениями элемент балки длиной ds и рассмотрим его деформационное состояние (рис. 102а). Справа показана схема деформации этого элемента в упрощенном виде, из которой следует, что

.

Тогда можем записать:

или, если учесть, что - удлинение волокна на расстояние у от Н.Л.; ; ао=у;

ОА= - радиус кривизны Н.Л., тогда , где величина - относительное удлинение волокна, находящегося на расстоянии у от нейтральной линии.

Итак, геометрическую зависимость представим в виде: .

Физическая сторона задачи.

Установив, что при изгибе волокна по высоте либо сжимаются, либо растягиваются, не оказывая влияния друг на друга, мы можем применить закон Гука при простом растяжении (сжатии), а именно:

.

Далее, используя выражение для , запишем:

.

Из этого выражения мы можем сделать вывод: величина напряжения по высоте меняется по линейному закону и прямо пропорциональна расстоянию волокна от Н.Л. и обратно пропорциональна радиусу кривизны ( и Е для каждой балки - величины постоянные). Для прямоугольного сечения по высоте показано на рис. 102в.

Геометрическую и физическую стороны увяжем между собой. Для этого запишем уравнения статического равновесия для отсеченной части балки (рис. 103):

1. ; .

Здесь , , тогда , а данное выражение есть статический момент площади поперечного сечения. Следовательно, нейтральная линия проходит через центральную ось, т.е. через центр тяжести сечения.

2. .

Момент от внешних сил будет уравновешиваться моментом от . Подсчитаем этот момент:

, подставим сюда , получим:

, но - момент инерции сечения.

Тогда ,

где : - жесткость балки при изгибе; - кривизна изогнутой оси балки.

Из полученного выражения момента можем выразить величину изогнутой оси балки:

Вернемся вновь к выражению для . Запишем:

.

Для сечений с центром тяжести, симметричным по высоте (рис. 104), максимальное напряжение будет при , т. е.

. Разделим числитель и знаменатель на , тогда получим:

, но из определения геометрических характеристик сечения выражение соответствует моменту сопротивления W и тогда

.

Кроме нормальных напряжений, в сечении балки возникают и касательные напряжения (в случае плоского изгиба).

Выясним закон их распределения по высоте сечения балки.

Из балки (рис. 105а) вырежем двумя поперечными плоскостями и одной продольной элемент a-n-m-d и рассмотрим его отдельно (рис. 105б).

На грани an действует напряжение

,

а на грани md

,

т. к. при плоском изгибе изгибающий момент меняется по длине балки.

На грани ad действует касательное напряжение, собранное с площадки , где b – ширина прямоугольного сечения балки.

Запишем равновесие элемента:

; ,

где: N и N₁ – равнодействующие нормальных напряжений на гранях an и md, соответственно. Вычислим их:

,

где - статический момент отсеченной части поперечного сечения.

Аналогично можем записать выражение для N₁ :

.

Подставим N и N₁ в уравнение равновесия:

.

Отсюда находим:

или

,

но , тогда

- формула Журавского (1856 г.).

Посмотрим, как изменяются касательные напряжения по высоте прямоугольного сечения (рис. 106).

Возьмем волокно на высоте y и распишем для него выражение для τ.

Q, J, b – величины для данного сечения постоянные.

S – статический момент сечения, расположенного выше значения y:

,

тогда

при ; ;

; .

График изменения касательных напряжений показан на рис. 106.

3. Деформация балки: прогиб балки и угол поворота сечения.

Теперь выясним зависимость прогиба балки и угла поворота сечения от изгибающего момента (рис. 107). Запишем выражение кривизны изогнутой оси балки, полученной нами ранее:

.

Кривизна, а в равной степени и прогиб зависят прямо пропорционально от изгибающего момента и обратно пропорционально от жесткости балки, где Е определяет материал балки, а J – ее размеры.

В то же время, из математики известна зависимость кривизны изогнутой линии от прогиба кривой:

.

Для жестких балок, используемых в строительстве, прогиб достаточно мал по сравнению с длиной балки. Поэтому выражением можно пренебречь.

Тогда

.

Но используя выражение (4) запишем:

,

т. е. вторая производная прогиба прямо зависит от величины изгибающего момента и обратно зависит от жесткости балки.

Знак (-) в выражении прогибов принимается, если выпуклость изогнутой линии совпадает с направлением оси y и изгибающий момент положителен.

Угол поворота φ есть tg угла, заключенного между касательной к изогнутой оси балки в сечении х и первоначальному положению оси балки

.

Ввиду малости этих углов, можем записать ,

т. е. угол поворота сечения есть первая производная прогиба балки.

Рассмотрим пример (рис. 108).

1. Опорные реакции нами уже были вычислены:

; .

2. Запишем выражения изгибающих моментов для каждого из двух участков:

I участок

.

II участок

.

Выражение для прогибов тоже запишем для каждого участка.

I участок:

II участок:

.

Интегрируя каждое выражение, получим:

Угол поворота на 1-ом участке .

То же на 2-ом участке .

Прогиб на первом участке .

То же на втором участке .

Постоянные интегрирования C₁, C₂, D₁, D₂ определяются из граничных условий:

1) х = 0 (на опоре А). y₀ = 0.

2) x = L (на опоре В). y_L = 0 .

На границе двух участков прогиб будет одинаковый, т. е.

3) y₁ = y₂ .

То же касается и углов поворота

4) φ₁ = φ₂ .

Запишем эти выражения:

1. y = 0 D₁ =0.

2. .

3. (x = a)

.

4. .

C₁ = C₂

Из 3-его уравнения: ; .

Из 2-го уравнения: ; .

Константы определены, значит найдутся и прогибы, и углы поворота на каждом участке.

6. Составные конструкции (системы)

и их расчеты

1. Основные понятия.

Составными конструкциями считаются конструкции, составленные из двух и более отдельных конструктивных элементов (дисков) типа балок, колонн, кривых брусьев, ферм различного очертания и назначения, ломаных брусьев (рам) и т. д., соединенных между собой связями.

Как мы уже знаем из кинематического анализа, два диска могут соединяться:

• одной связью (рис. 109а), в которой при ее сечении возникает только одно продольное усилие и оно будет направлено в месте разреза в противоположные стороны (рис. 109б);

• двумя связями (рис. 110а), в которых после их сечения возникнут два продольных усилия N₁ и N₂ (рассмотрим только левую часть, рис. 110б). Проецируя эти усилия на вертикальную и горизонтальную составляющие, мы получаем продольное усилие – N и перерезывающую силу Q (рис. 110в).

Можем сделать вывод: две связи, соединяющие два диска, образуя треугольник (рис. 110а), равноценны шарниру (рис. 111), при сечении которого возникает два внутренних усилия (рис.110в). Внимание! Момент в шарнире равен нулю ( ! ).

Следует помнить, что два диска, соединенные двумя связями, расположенными параллельно (рис. 112), дают мгновенно изменяемую систему;

• тремя связями (рис. 113), в которых при их сечении возникнут 3 усилия, и при разложении их на вертикальную и горизонтальную составляющие дают продольное усилие – N, перерезывающую силу Q и, что особенно важно, момент – M (рис. 114) противоположных направлений.

Следует отметить, что соединение двух дисков тремя связями равносильно жесткому соединению. Жесткое соединение может производиться с помощью сварки, пайки, заклепок, склеивания и т. д.

Рассмотрим простейшую систему, состоящую из трех дисков, соединенных между собой шарнирно в треугольник (рис. 115). Получим геометрически неизменяемую систему. Она будет неподвижной, если один из дисков мы будем считать землей. Такую систему назовем арочной (рис. 116) – здесь шарниры А и В заменены двухстержневыми опорами.

Диски могут принимать различное очертание и структуру, и, в зависимости от их конструктивных особенностей, мы получаем;

а) трехшарнирную арку (рис. 117).

В этом случае диски имеют криволинейное очертание – дуга окружности, параболы, эллипса и другой кривой.

б) трехшарнирную раму (рис. 118).

Здесь диски представляют собой ломаные стержни (элементы рамы).

в) трехшарнирную ферму ( рис.119).

Из рисунка видно, что диски представлены отдельными фермами различного очертания.

Если в арочной системе шарнир С будет находиться по отношению к шарнирам А и В ниже (рис. 120а), то система носит название – висячая система. В висячих системах диски, как правило, являются гибкими стержнями (тросами) (рис. 120б).

Составная система, в зависимости от вида и количества дисков, может представлять составную конструкцию (рис. 121а, б, в) любого очертания и назначения.

2. Расчет составных конструкций

Под расчетом конструкций, как мы уже отмечали, понимаем определение внутренних усилий в сечениях всех элементов конструкции, т. е. распределение внутренних усилий (Q, N, M) по длине конструкций, составляющих составную систему.

Началом расчета конструкций при заданной нагрузке является определение опорных реакций, и ведется оно тремя приемами (путями):

1. использование свойств шарнира – изгибающий момент в шарнире равен нулю;

2. расчленение конструкции на ее составные элементы. Расчленение, как правило, ведется по шарнирным соединениям;

3. расчленение конструкции на отдельные элементы с последующим построением «этажной схемы».

Нужно отметить, что для одних конструкций можно использовать все три приема в равной степени, для других – только один из приведенных.

Обратимся к примерам.

2.1. Двухдисковая составная система.

Арка (рис. 122). Определение опорных реакций для этой составной системы рассмотрим первым и вторым приемами:

А) Использование свойства шарнира.

Используя равновесие системы, составляем уравнения статики:

1. ∑ х = 0; Н_А – Н_С = 0.

2. ∑ y = 0; R_A – q · 6 – P + R_C = 0.

3. ∑ M_А = 0; .

В эти уравнения вошли четыре неизвестных реактивных усилия - Н_А ; Н_С ; R_A; R_C.

В качестве четвертого уравнения используем свойство шарнира – изгибающий момент (внутреннее усилие) в шарнире равен нулю.

Запишем значение изгибающего момента в шарнире В левой (или правой) части конструкции:

4. ; .

Из полученных уравнений определяются все опорные реакции.

Первое уравнение определяет, что Н_А = Н_С.

Из третьего уравнения определяем

R_C = (1*6*6/2 + 2*9)/ 12 = 3,0 (kH).

Второе уравнение позволяет найти

R_A = 1*6 + 2 – 3,0 = 5,0 (kH).

И из четвертого уравнения определяется

Н_С = ( 3*6 + 2*3) / 4 = 6 (kH).

Б) Второй прием определения опорных реакций построен на расчленении

составной системы на отдельные ее части.

Рассечем арку по шарниру В (рис. 122), где возникают два неизвестных реактивных усилия H_B и R_B, взаимно равных между собой, но имеющих противоположные направления. Скажем, R_B действует на левую часть арки снизу вверх, а на правую часть арки – сверху вниз (рис. 123).

Учитывая, что до расчленения система была в равновесии, то после ее расчленения обе ее части остаются в равновесии. На этом основании составляем уравнения равновесия для каждой части расчлененной арки (рис. 123):

а) Равновесие левой части арки:

1. ∑ х = 0; Н_А – Н_В = 0.

2. ∑ y = 0; R_A – q · 6 + R_В = 0.

3. ∑ M_В = 0; .

б) Равновесие правой части арки:

1. ∑ х = 0; Н_В – Н_С = 0.

2. ∑ y = 0; -R_В – P+ R_C = 0.

3. ∑ M_В = 0; .

В общем случае получили шесть уравнений с 6-тью неизвестными. Решение таких систем с использованием машин удобнее представить в матричной форме. Для нашего примера полученные уравнения представим в виде:

	НА	НВ	RA	RB	HC	RC				P
1	1	-1						HA		0
2			1	1				HB
3		-4	6				x	RA	=
4		1			-1			RB		0
5				-1		1		HC		P
6					-4	6		RC

(в незаполненных клетках следует читать ноль).

Левый множитель представляет собой квадратную матрицу 6 порядка, и назовем ее матрицей коэффициентов при неизвестных – [A]; второй множитель представляет матрицу столбец неизвестных – [X], и правую часть этой системы уравнений назовем как матрицу столбец нагрузки – [P].

Тогда запись системы уравнений принимает компактный вид:

Матричное решение запишется:

или ,

где - есть обратная матрица матрицы .

Решение системы уравнений любым способом дает те же результаты:

R_A = 5 (kH), R_C = 3 (kH),

H_A = H_C = 6 (kH).

В определении внутренних усилий в трехшарнирных арках имеются некоторые особенности, вызванные криволинейностью стержней. На этих особенностях мы и остановимся.

1) Изгибающий момент в арках.

Возьмем для примера сечение «К» на расстоянии «х» от опоры А (рис. 122) и рассмотрим ее левую часть относительно сечения (рис. 124а).

Сумма моментов всех сил относительно точки «К» запишется:

.

Отсюда

.

Выражение ( ) есть изгибающий момент простой балки (рис. 124б), получаемой из заданной арки при замене ее криволинейной оси на прямую, совпадающую с положением оси х.

Тогда выражение для изгибающего момента можем представить в виде:

б) Перерезывающая сила.

Спроецируем все силы (рис. 124а) на направление, перпендикулярное касательной к арке в точке К

.

Преобразуем выражение

.

Таблица 1

х (м)	Y (м)					(кг)
0	0	1,9	530	0,8	0,6	5	4,0	3,0	-2,4	1,8	0	0	0,60	0,0	-5,80
2	2,2	0,9	41038	0,66	0,74	3	1,99	2,24	-1,99	2,24	8,0	8,0	0,25	1,33	-4,23
4	3,5	0,4	23056	0,40	0,91	1	0,41	0,92	-1,22	2,74	12,0	12,0	-0,30	1,33	-3,15
6	4,0	0	0	0	1,0	-1	0,0	-1,0	0	3,0	12,0	12,0	-1,0	0,0	-3,00
8	3,5	-0,4	-23056	-0,40	0,91	-1	0,41	-0,91	1,22	2,74	-10,67	-10,0	0,31	-0,67	-3,15
9	3,0	-0,7	-33042	-0,55	0,83	-1 -3	0,56 1,68	-0,83 -2,50	1,67	2,5	9,0	9,0	0,84 -0,83	0,0	-3,06 -4,17
10	2,2	-0,9	-41038	-0,66	0,74	-3	1,99	-2,24	1,99	2,24	-6,67	6,0	-0,25	-0,67	-4,23
12	0	-1,3	-530	-0,8	0,6	-3	2,40	-1,80	2,4	1,8	0,0	0,0	0,6	0,0	-4,20

Сумма в скобках есть перерезывающая сила простой балки (рис. 124б). Тогда можем записать

в) Продольное усилие

Проецируем силы (рис. 124а) на направление касательной:

.

Отсюда, с учетом преобразований ,запишем:

.

Как и выше, выражение в скобках есть перерезывающая сила , тогда:

Для арки (рис.122), очертание которой соответствует квадратной параболе вида:

,

примем: х = 0; 2; 4; 6;8; 9; 10; 12, что соответствует сечениям 1; 2; 3; 4; 5; 6; 7; 8 (рис.125а).

Согласно полученным выражениям для изгибающего момента, перерезывающей и продольной силам в произвольном сечении нам потребуется вычислить значения изгибающего момента и перерезывающей силы для простой балки в отмеченных сечениях (рис. 125б). Эпюры Q^б и M^б для такой балки построены и показаны на рисунке 125 в,г), соответственно.

Для изгибающего момента вычисляем координату y из выражения очертания арки, задавая соответствующие значения х.

Для перерезывающих и продольных сил в отмеченных сечениях арки нам потребуются значения Cos α и Sin α.

Для их вычисления определим вначале tgα как первую производную уравнения оси арки, т. е.:

.

По значению tga для каждого сечения определяем значение α, а затем и значение Cos α и Sin α.

Для ручного счета (прикидочного расчета) ход решения удобно вести в табличной форме (табл. 1).

По данным расчета, эпюры М, Q, N для арки построены и показаны на рисунке 125 д,е,ж, соответственно.

Отметим (!):

а) все эпюры криволинейны независимо от вида загружения, что обуславливается криволинейностью оси арки;

б) эпюра N по длине арки отрицательная, т.е. ось арки испытывает только сжимающие усилия.

2.2. Трехдисковая составная система (рис. 126).

Кинематический анализ дает

n = 3*3 – 2*2 – 5 = 0.

Определение опорных реакций R₈, R₆, R₁, H₁, M₁ проведем всеми тремя приемами:

а) Свойство шарнира.

Шарнир 5 элемента 7-8-9-5 (рис. 126).

М₅ = 3*5*2,5 – 10*4 – R₈ *3 = 0, или R₈ = - 0,83.

Направлением опорной реакции мы ошиблись – она будет направлена вниз.

Шарнир 2 всей нижней части конструкции

М₂ = R₈ *1 – 3*5*0,5 + 10*7 - R₆ *5 – 2*3*1,5 = 0 или

- 0,83*1 – 7,5 + 70 - R₆ *5 – 9 = 0, откуда

R₆ = 10,53

Реакции R₁, H₁, M₁ определяются из равновесия всей конструкции (системы):

H₁ + 2*3 – 10 = 0 откуда Н₁ = 4.

R₁ + 6 – 5 - 3*5 + R₈ + R₆ = 0 или

R₁ = - 6 + 5 + 15 + 0,83 - 10,53 = 4,3.

= 0,

M₁ – 6*5 – 2*3*1,5 + 5*3 – R₆*8 + 10*7 – R₈*2 + 3*5*2,5 = 0 или

М₁ = 30 + 9 – 15 + 10,53*8 – 70 – 0,83*2 – 37,5 = - 0,92.

б) Расчленение системы на элементы, ее составляющие.

Первый элемент 1-2-3 (рис. 127а). Составляем уравнения равновесия для данного элемента:

. Н₁ + Н₂ = 0.

. R₁ + R₂ + 6 (kH) = 0.

. M₁ – R₂*3 – 6*5 = 0.

Второй элемент 2-4-5-6 (рис. 127б).

Обратим внимание на направление реакций Н₂ и R₂. Уравнения равновесия запишутся:

. Н₂ – 2*3 – Н₅ = 0,

. – R₂ – 5 + R₅ + R₆ = 0,

. 2*3*1,5 + R₅ *2 + H₅*3 + R₆*5 = 0.

Третий элемент 5-9-8-7 (рис. 127в).

. 10 + Н₅ = 0,

. R₈ - R₅ – 3*5 = 0,

R₈*3 + 10*4 – 3*5*2,5 = 0.

Последняя группа уравнений позволяет определить реакции опор третьего элемента:

Н₅ = - 10 (kH); R₈ = - 0,83 (kH); R₅ = - 15,83 (kH).

Зная реакции третьего элемента, перейдем к определению реакций второго элемента:

H₂ = - 4 (kH); R₂ = - 10,3 (kH); R₆ = 10,53 (kH).

Вычисляем реакции первого элемента:

H₁ = 4 (kH); R₁ = 4,3 (kH); M₁ = -0,9 (kH*м).

В данном примере мы определили реактивные усилия без решения системы 9 уравнений с 9-тью неизвестными.

в). Разбиение системы на элементы с последующим построением «этажной» схемы.

В конструкции (рис. 126) основным элементом (балкой) будет 1-2-3. К нему в точке 2 будет подвешиваться (не опираться) элемент 2-4-5-6 ( по принципу «турника»), а к этому элементу, в свою очередь, будет подвешиваться элемент 5-9-8-7. Расчет в этом случае ведется с нижнего элемента, как это мы уже наблюдали выше (в пункте б).

Эпюры внутренних усилий построим для каждого элемента, причем реактивные усилия прикладываем к элементу с учетом их истинного направления, т.е., если получили знак минус, то к элементу их необходимо приложить в другом направлении.

1 элемент (1-2-3, рис. 128).

2 элемент (2-4-5-6, рис. 129).

Приведем вычисление характерных точек для изгибающего момента:

М_4-2 = 4*3 + 2*3*1,5 = 21 (кНм),

М_С = 4*1,5 + 2*1,5*0,75 = 8,25 (кНм).

М_5-6 = 10,53*3 = 31,59 (кНм),

М_4-6 = 10,53*5 – 15,83*2 = 21 (кНм).

3 элемент (5-9-8-7, рис. 130).

Приведем вычисление характерных точек:

для перерезывающей силы

сечение 8 бесконечно близко слева Q₈ = 3*2 = 6 (кН);

сечение 8 бесконечно близко справа Q₈ = 3*2 + 0,83 = 6,83 (кН);

сечение 9 для участка 7-9 Q_9-7 = 3*5 + 0,83 = 15,83 (кН).

для изгибающего момента

сечение 8 участка 8-7 М_8-7 = 3*2*1 = 6 (кНм);

сечение 9 участка 9-7 М_9-7 = 3*5*2,5 + 0,83*3 = 40 (кНм).

Для конструкции в целом нужно только состыковать все эпюры в одно целое.

2.3. Составная многопролетная балка (рис. 131 а).

Определение опорных реакций можем производить всеми тремя приемами, но, как правило, для таких балок используется прием построения «этажной» схемы. Расчленим балку по шарнирам 3, 5, 6. Кинематический анализ каждого ее элемента дает, что балка 6-7 является геометрически неизменяемой и неподвижной и считается основной. Балка 5-6 имеет три степени свободы. Придадим ей три опорных стержня и концом 6 обопрем на балку 6-7, а концом 5 - на балку 3-4-5, которая, в свою очередь, имеет две степени свободы, и концом 3 будет опираться на балку 1-2-3. Балка 1-2-3 имеет одну степень свободы и для ее неподвижности добавим один горизонтальный опорный стержень. Это позволит считать балку 1-2-3 также основной. Этажная схема представлена на рисунке 131б.

Этажная схема позволяет выявить очередность расчета, помня о том, что нагрузка верхних «этажей» передается на нижние, но не наоборот. Схема передачи нагрузки от балки к балке показана на рисунке 131 в.

Следовательно, первой будет рассчитываться верхняя балка 5 – 6. Затем рассчитываются балки второго уровня: балка 3 – 4 – 5 и балка 6 – 7. И последней в нашем примере – балка 1 – 2 – 3. Итак, для каждой балки с учетом очередности составляются уравнения статики и определяются реактивные усилия.

Балка 5-6

Н₆ = 0,

R₅ *6 + R₆ - 3*3 = 0.

R₅*6 – 3*3*1,5 = 0. R₅ = 2,25 (kH), R₆ = 6,75 (kH).

Балка 3-4-5

Н₃ = 0.

R₃ + R₄ -2*7 – R₅ = 0.

R₃*5 + R₅*2 – 2*7* 1,5 = 0. R₃ = 3,3 (kH), R₄ = 12,95 (kH).

Балка 6-7

Н₇ = 0.

R₆ + 3*5 – R₇ = 0.

R₆*5 + 3*5*2,5 + M₇ = 0. R₇ = 21,75 (kH), M₇ = -71,25 (kHм).

Балка 1-2-3

Н₁ = 0.

R₁ + R₂ – 10 – R₃ = 0.

R₂*6 - 10*3 – R₃*8 = 0. R₁ = 3,9 (kH), R₂ = 9,4 (kH).

Построение эпюр внутренних усилий можем вести для балки в целом, а можем вычислить внутренние усилия для каждой балки отдельно и затем построить их на единой оси заданной балки (рис. 132).