3. Расчетная схема сооружений и их элементов

1. Суть расчетной схемы (модели).

Расчетная схема сооружения есть идеализированная (упрощенная) его схема. В нее не входит форма поперечного сечения элементов, его составляющих, а только их геометрические характеристики (площади сечения, моменты инерции и т. д.). Обратимся к примерам.

Балка – как наиболее часто встречающийся элемент сооружения представляет собой линию (ее ось), опирающуюся на опоры в виде отдельных

стержней (рис. 57). Нагрузка прикладывается по месту ее приложения.

Рама. Схема рамы представляется ее срединной линией с передачей нагрузки так, как она приложена (рис. 58). Размеры конструкций принимаются по ее срединной линии.

Ферма. Жесткое соединение стержней в узлах фермы заменяется шарнирным, а сами стержни – осевыми линиями. Опоры принимаются в виде отдельных стержней (рис. 59). Нагрузка прикладывается только в узлах.

Фермы классифицируются:

• По характеру очертания поясов:

а) стропильная (треугольная – одно - или двускатная, рис. 60а);

б) полигональная (верхний пояс представлен в виде ломаной прямой, рис. 60б);

в) сегментная (арочная), верхний пояс выполняется в виде дуги (кривой линии, рис. 60 в);

г) ферма с параллельными поясами (верхний и нижний пояса параллельны, рис. 60г).

• По характеру приложения нагрузки:

а) ферма с ездой по верхнему поясу (нагрузка прикладывается в узлах верхнего пояса);

б) ферма с ездой по нижнему поясу (нагрузка прикладывается в узлах нижнего пояса).

• По назначению:

а) балочная ферма используется для перекрытия пролетов. Она может опираться на две опоры и может быть консольной;

б) крановая – ферма подъемных строительных кранов;

в) опорная ферма – ферма опоры линий электропередач, колонн промышленных зданий, пилонов висячих мостов, опор (колонн) строительных конструкций.

Расчетные схемы других сооружений мы рассмотрим по мере изучения методов их расчета.

4. Сечения элементов конструкции и

их геометрические характеристики

1. Вводная часть

Как мы уже видели, поперечное сечение строительных конструкций (стержней, балок и т. д.) может быть от прямоугольника до мощного составного в виде сочетания прямоугольников, уголков и т. д. (рис. 61).

Поперечное сечение любого очертания характеризуется:

• величиной площади;

• статическим моментом;

• положением центра тяжести (продольная ось стержня (бруса) проходит по центру тяжести сечения);

• моментом инерции;

• моментом сопротивления;

• радиусом инерции.

Рассмотрим отмеченные характеристики на примере составного сечения, приведенного на рисунке 62.

2. Площадь поперечного сечения

Величина площади составного сечения равна сумме площадей элементов его составляющих, т. е.

,

где: F_i - площадь i-ой (отдельной) фигуры, входящей в составное сечение.

Вычисляем площади фигур составного сечения (рис. 62):

,

,

.

Общая площадь сечения .

3. Статический момент

Рассмотрим произвольное сечение площадью F (рис. 63). В плоскости сечения проведены оси x, y. Возьмем элементарную площадку dF и определим ее координаты: x и y от ее центра тяжести. Запишем произведение площадки dF на ординату – y и обозначим это произведение через , т.е.

.

Это и есть статический момент элементарной площади относительно оси х.

Просуммируем статический момент от всех элементарных площадок данного сечения и в пределе получим:

.

аналогично запишем выражение статического момента относительно оси y:

.

Результат интегрирования дает:

и ,

где : F – площадь поперечного сечения; y₀ и x₀ – соответственно, координаты центра тяжести данного сечения относительно выбранной системы координат.

Статический момент простых фигур.

Прямоугольник (рис. 64).

Подсчитаем статический момент прямоугольника относительно оси Х:

S_x = F * y_ц.т.,

где F = b*h и y_ц.т. = h/2, тогда S_x = b*h² /2.

Аналогично вычисляется статический момент относительно оси Y:

S_y = h*b²/2.

Треугольник (рис. 65).

Относительно произвольных осей Х и Y статический момент треугольника запишется:

S_x = F* y _ц.т. = (b*h/2)*h/3 = b*h²/6;

S_y = F* x_ц.т. = (b*h/2)*2*b/3 = b²*h/3.

Следовательно, для вычисления величины статического момента простых фигур относительно произвольно выбранной системы координат достаточно перемножить площадь сечения (фигуры) на расстояние до центра тяжести фигуры.

Статический момент относительно центральных осей (осей, проходящих через центр тяжести сечения) равен нулю (рис 64).

S_xо =(b*h/2)*h/4 – (b*h/2)*h/4 = 0.

Размерность статического момента, как это не трудно видеть, является м³,

см³ и т. д.

Статический момент составного сечения вычисляется как сумма статических моментов отдельных фигур данного сечения, т.е.

и .

Обратимся к примеру (рис. 62). Оси координат проведем через точку А, тогда статические моменты относительно этих осей примут вид:

, .

4. Центр тяжести сечения

Из выражений статического момента следует, что координаты центра тяжести сечения (в том числе составного сечения) равны:

; .

Вычисляем положение центра тяжести составного сечения (рис. 62):

;

.

5. Момент инерции сечения

Различают следующие моменты инерции сечения:

- осевой момент инерции;

- центробежный момент инерции;

- полярный момент инерции.

Осевым моментом инерции сечения называется сумма произведений площадей элементарных площадок dF на квадраты их расстояний до этой оси (рис. 66), т. е.

-

момент инерции сечения относительно оси х;

-

момент инерции сечения относительно оси y.

Центробежным моментом инерции сечения называем сумму произведений площади элементарных площадок dF на координаты их расстояний от осей x, y;

.

Полярным моментом инерции называется сумма произведения площадей элементарных площадок dF на квадрат расстояния от площадки до точки (начало координат) – полюса (рис. 66):

.

По теореме Пифагора , подставляя в выражение полярного момента инерции, получим:

или .

Моменты инерции простых фигур

Прямоугольник (рис. 67).

а) Осевой момент инерции сечения относительно оси х. Выделим площадь сечения на высоте у. Тогда:

.

Аналогичные рассуждения приведут к выражению для момента инерции сечения относительно оси у:

.

б) Центробежный момент инерции прямоугольника относительно осей х, у (рис. 68). Запишем площадь с координатами х, у и составим выражение для центробежного момента:

.

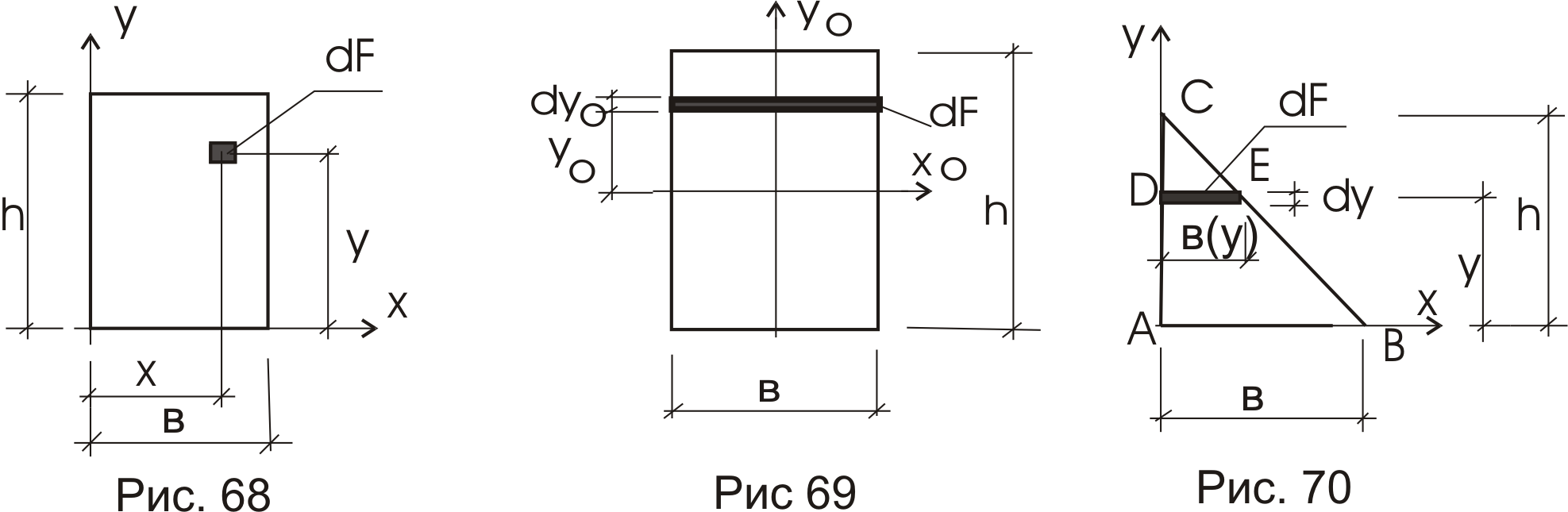
в) Осевой момент инерции сечения относительно оси х₀ (центральной оси прямоугольника – рис.69). Имеем . Тогда

.

Те же рассуждения приведут к выражению момента инерции прямоугольника относительно оси :

.

Центробежный момент инерции прямоугольника относительно осей Хо, Уо , являющимися главными центральными осями, будет равен нулю, т.е.

.

Треугольник (рис. 70).

а) Момент инерции относительно оси х:

.

Здесь - (из подобия треугольников АВС и DЕС).

Тогда

.

Аналогичное решение для момента инерции относительно оси у:

.

б) Центробежный момент инерции треугольника (рис. 70) относительно осей х, у, совпадающих с положением катетов.

,

где: ;

- расстояние от оси х до центра тяжести площадки ;

- расстояние от оси у до центра тяжести площадки и оно будет равно

; в свою очередь - как было показано выше (рис. 70),

тогда

.

Круг (рис. 71).

Для круга находим полярный момент инерции относительно его центра:

.

Возьмем полоску (окружность) с толщиной d, тогда . Запишем выражение полярного момента инерции:

.

Если учесть то

Моменты инерции круга относительно центральных осей равны J_x = J_y.

Из выражения J_x + J_y = J получим 2J_x = J или

.

Моменты инерции сечения при параллельном переносе осей.

Рассмотрим сечение бруса (рис. 72). Для данного сечения известны , т.к. х₀, у₀ - оси центральные. Нужно определить моменты инерции сечения относительно произвольных осей х, у, отстоящих от центральных на расстоянии «а» и «в» соответственно (рис. 72).

а) Момент инерции сечения относительно оси х:

.

Здесь y = a+y_0., тогда:

.

В полученном выражении:

- площадь сечения;

статический момент сечения относительно оси x₀ – Sx₀;

момент инерции сечения относительно оси х₀ .

После отмеченных подстановок получаем:

.

б) Момент инерции сечения относительно оси у.

В этом случае в выражении координата . После аналогичных преобразований получим:

.

в) Центробежный момент инерции относительно осей х,у:

, подставляя сюда значения х и у (рис. 72) получим:

,

принимая во внимание, что ,

, ,

выражение центробежного момента инерции примет вид:

.

Во всех трех выражениях инерции присутствуют S_y0 и S_x0, которые, как мы уже отмечали, для центральных осей равны нулю, и тогда моменты инерции относительно произвольных осей по отношению к центральным запишутся:

; ; .

Вернемся к примеру (рис. 62).

Требуется вычислить моменты инерции составного сечения (рис. 62) относительно центральных осей. Координаты центра тяжести данного сечения нами были уже подсчитаны: х₀ = 10,88 см; у₀ = 9,46 см. Центральные оси составного сечения будут считаться произвольными по отношению к центральным осям отдельной фигуры, входящей в составное сечение.

а) Момент инерции составного сечения будет равен сумме моментов инерции отдельных фигур, т. е.

где: а₁ = 12,5 – 9,46 = 3,04; а₁² = 9,24

а₂ = 7,5 – 9,46 = -1,96; а₂² = 3,84

а₃ = 2,5 – 9,46 = -6,96; а₃² = 48,44

Тогда:

21708,88 (см⁴).

б) Аналогично подсчитывается момент инерции Jy₀:

.

Здесь: ; ; ;

b₁ = 5 – 10,88 = -5,88; b₁² = 34,57

b₂ = 14 – 10,88 = 3,12; b₂² = 9,73

b₃ = 25,5 – 10,88 = 14,62; b₃² = 213,74

29970,18

в) Для центробежного момента инерции

.

Здесь: Jx_iy_i – центробежный момент инерции относительно центральных осей отдельной фигуры, являющихся осями симметрии, равен нулю, т.е. для данного примера

;

остальные параметры нам известны. Произведем вычисления:

-12833,87 (см⁴).

Целесообразно рассмотреть еще пример, результаты которого используются в практике расчета, нахождение центробежного момента инерции относительно центральных осей прямоугольного треугольника по отношению к осям, проходящим вдоль катетов (рис. 73). Выражение для центробежного момента инерции

, здесь

; ; ; , тогда

.

Моменты инерции сечения при повороте координатных осей.

Рассмотрим сечение (рис. 74). Площадка dF с координатами x, y при повороте осей на угол  получит новые координаты:

Найдем моменты инерции относительно новых осей через оси x, y:

или

.

По аналогии, проведя подобные вычисления, получим:

Для центробежного момента инерции запишем:

.

Из тригонометрии:

; ,

тогда, подставив эти значения , получим:

.

С учетом преобразований запишем окончательно значения моментов инерции :

.

Полученные выражения позволяют нам перейти к главным центральным осям сечения.

Главные центральные оси характеризуются:

• равенством нулю центробежного момента инерции J_xy = 0;

• один из моментов инерции достигает максимального значения, тогда другой момент инерции имеет минимальное значение, и они называются главными.

Выражение для приравняем нулю:

.

Разделим выражение на Соs 2 и умножим на 2, получим:

.

Отсюда мы определяем угол поворота центральных осей до положения главных центральных:

.

Этому углу поворота будут соответствовать максимальное и минимальное значения моментов инерции:

Знак (+) перед радикалом соответствует максимальному значению, а знак (-) - минимальному значению момента инерции.

Пример (рис.62 ).

Для этого составного сечения мы вычислили:

; ; .

Для положения главных центральных осей подсчитаем угол наклона их к осям x₀, y₀ по выражению , т. е.

.

По этому значению определяем:

); ( .

6. Момент сопротивления

В расчетах, особенно при изгибе, большую роль играют моменты сопротивления сечения.

Момент сопротивления относительно какой-либо оси есть отношение момента инерции относительно этой же оси к расстоянию до наиболее удаленной от нее точки, т. е.

; .

Так, для прямоугольника момент сопротивления примет вид:

; .

Для круглого сечения:

.

Для составного сечения (рис. 2) моменты сопротивления вычисляются:

а) относительно центральных осей :

; .

б) относительно главных центральных осей:

; .

7. Радиус инерции сечения

В выражениях моментов инерции сечения , величины у и х есть расстояния от осей до центра тяжести площади dF. Усредним эти расстояния и примем и .

Для простых сечений (прямоугольник, квадрат) – это расстояния до центра тяжести сечения.

Величины i_x и i_y, взятые в квадрат, и есть радиусы инерции сечения, т. е. i_x² – радиус инерции относительно оси х, i_y² –радиус инерции относительно оси y.

Подставим в выражения моментов инерции величин и .

Получим: и , тогда

.

Для нашего составного сечения (рис. 62) радиусы инерции будут равны:

; .