Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

лекции для архитекторов.doc

Скачиваний:

Добавлен:

01.03.2025

Размер:

20.51 Mб

Скачать

☆

1 / 121 2 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ`

КАЗАНСКИЙ ГОСУДАРСТВНННЫЙ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

УНИВЕРСИТЕТ

В.Г.Немов

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Допущено

Учебно-методическим объединением по

образованию в области архитектуры в

качестве учебного пособия для студентов

вузов, обучающихся по направлению

«Архитектура»

Казань

2006

УДК 531.8 + 624. 042 (075.32)

ББК 22.21

Н 50

Н 50 Немов В.Г. Теоретическая механика: Учебное пособие. Казань: КГАСУ, 2006 г. – 145 с.

ISBN 5-7829 – 0158 – 6

Печатается по решению Редакционно-издательского совета Казанского государственного архитектурно-строительного университета

Учебное пособие предназначено для студентов архитектурно-строительных вузов, изучающих курс теоретической механики, включающий в себя разделы: теоретической механики, сопротивления материалов и строительной механики. В пособии рассмотрены основные аксиомы и основные понятия силы, момента и уравнения статики, основы расчета упругого тела (балки) на растяжение, изгиб, даны основные методы расчета строительных конструкций (балок, арок, ферм, рам и их комбинаций) на статическую и подвижную нагрузки как статически определимых, так и статически неопределимых систем. Теоретический материал сопровождается примерами расчета. Пособие соответствует программе курса и требованиям Государственных образовательных стандартов.

Табл. 1. Илл. 250. Библиогр. 10 наим.

Рецензенты:

1-ый проректор ННГАСУ, член-корреспондент РААСН, профессор

В.Н.Бобылев

заведующий кафедрой теории сооружений и строительной механики

ННГАСУ, кандидат технических наук, доцент Б.Б.Лампси

заведующий кафедрой сопротивления материалов и основ теории упругости КГАСУ , профессор Р.А.Каюмов

Общая редакция – заведующий кафедрой строительной механики

КГАСУ, профессор В.Н.Сучков

JSBN 5-7829-0158-6 УДК 531.8 + 624.042 (075.32)

ББК 22.21

строительный университет, 2006

Первоначальные понятия и определения

1.1 Конструкции и их элементы

Вопросы, рассматриваемые в курсе теоретическая механика, читаемом для архитектурных специальностей, в конечном итоге сводятся к расчету строительных конструкций, которые лежат в основе образования архитектурных форм зданий и сооружений.

Строительные конструкции, в зависимости от их геометрии, можно разложить на следующие простые элементы.

БАЛКА – прямой элемент, длина которого значительно больше размеров поперечного сечения. Длина ( L ) называется пролетом (рис. 1а), а поперечное сечение 1-1 может быть (рис. 1б):

прямоугольником с размерами а * h (на ранней стадии применения балка вырубалась из камня, позднее изготавливалась из дерева, бетона, железобетона),

- тавровым сечением (бетон, железобетон, прокат) (рис. 1в),

- двутавром, швеллером, а также их комбинациями.

Балка, в зависимости от назначения и соотношений размеров, может называться: перемычкой, ригелем, прогоном, стержнем, брусом.

ПЛИТА – балка, у которой ширина поперечного сечения значительно больше ее высоты (рис. 2).

КОЛОННА (стойка –рис. 3) – конструкция типа балки, устанавливаемая вертикально. Колонна воспринимает, как правило, сжимающие усилия. Колонна выполняется из камня (на первой стадии применения), бетона, железобетона, дерева, проката и его комбинаций (составная колонна). Сечение колонны может быть как и у балки, в том числе и круглым.

АРКА – конструкция типа балки криволинейного очертания (рис. 4). Сечение арки может быть таким же, как и у балки. Иногда к пяте от замка сечение арки меняет свои размеры: h_п > h_з. Очертание арки может быть по дуге окружности, эллипса или по дуге другой кривой. Первоначально арка выполнялась из камня и ее очертание подбиралось так, чтобы она по своей длине работала только на сжатие. Арка используется для перекрытия пролетов мостов, помещений зданий, оконных и дверных проемов.

РАМА – конструкция, представляющая собой ломаную балку различного очертания (рис. 5). Соединение балок (стержней) в узлах рамы может производиться жестко или шарнирно. Сечение рамы изготавливается из проката, а также из железобетона.

ФЕРМА –конструкция, составленная из отдельных балок (стержней) различного поперечного сечения из дерева, а позднее - из металлопроката, железобетона, труб и других материалов. Стержни прямолинейного очертания соединяются между собой в узлах так, чтобы оси стержней, сходящиеся в узел, пересекались в одной точке. (На практике металлические стержни в ранний период ее изготовления крепились в узле с помощью заклепок. В настоящее время соединения производятся с помощью сварки).

Ферма характеризуется пролетом и высотой (рис. 6). Стержни фермы, располагаемые внизу, образуют нижний пояс. Стержни, располагаемые вверху фермы, образуют верхний пояс. Вертикальные стержни называются стойками, а наклонные - раскосами.

Комбинация стоек и раскосов образует решетку фермы. Расстояние между узлами фермы носит название панель фермы, а стержни, находящиеся в зоне панели, именуются стержнями соответствующей панели.

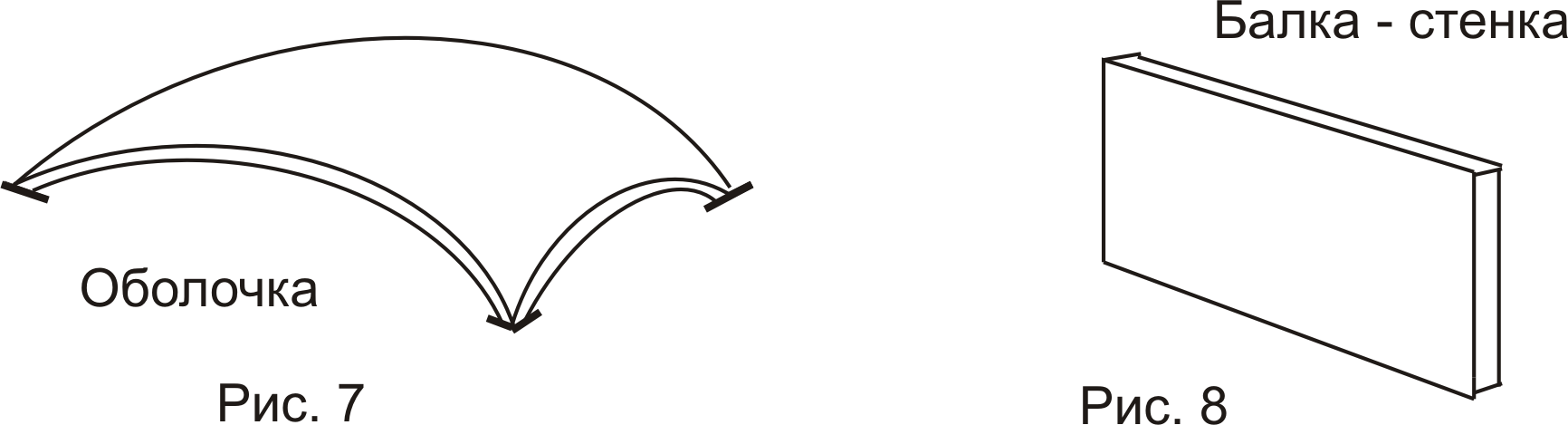
ОБОЛОЧКИ и ПЛАСТИНЫ – конструкции, у которых один размер по отношению к двум другим значительно меньше (рис. 7).

Пластина, устанавливаемая вертикально, носит название балка-стенка (рис. 8). Все эти конструкции используются как несущие и ограждающие и выполняются из железобетона, металла и других новых прочных материалов.

ТЕЛА и СПЛОШНЫЕ СРЕДЫ – конструкции, размеры которых во всех направлениях одного порядка.

1.2 НАГРУЗКИ

Расчет конструкций производится либо от заданной нагрузки, либо под размеры конструкции (площади поперечных сечений заданы) вычисляются величины нагрузки.

Нагрузки разделяются:

по времени действия на:

- постоянные (собственный вес конструкции, вес оборудования),

- временные (нагрузка от снега, ветра, от технического персонала и т.д.),

по характеру действия (загружения) на:

- сосредоточенные,

- распределенные, а также

парой сил (моментом).

1. СОСРЕДОТОЧЕННАЯ нагрузка характеризуется силой.

Сила – вектор определенной величины, измеряемый эталоном сил – н (ньютон), - кн (килоньютон), - мн (меганьютон). В технике еще используется измерение силы в кг (килограмм). Сила 1 кг = 9,81 н или 1 н = 0,102 кг.

Сила характеризуется (рис. 9а): точкой приложения -А (точка касания двух тел); направлением (вектор А-В); линией действия n-n (продолжением вектора А-В); модулем (величиной вектора А-В).

Система сил – совокупность сил, действующих на тело (конструкцию). Системы сил подразделяются на:

сходящиеся (линии действия сил сходятся в одной точке, рис. 9б);
параллельные (линии действия сил параллельные, рис. 9в);
случайные (силы располагаются произвольно, рис. 9г);
плоские силы (силы, расположенные в одной плоскости), в противном случае система сил – пространственная.

2. РАСПРЕДЕЛЕННАЯ нагрузка (рис. 10) характеризуется величиной (интенсивностью), приходящейся на единицу длины, т.е. q н/см (или кН/м). Данная нагрузка возникает прежде всего от веса конструкций:

для балки постоянного поперечного сечения нагрузку можем представить как нагрузку равной интенсивности (рис. 10б).

Распределенную нагрузку с постоянной интенсивностью называют равномерно-распределенной, а нагрузку от веса снега и других загружений с переменной интенсивностью q (x) - распределенной нагрузкой.

3. Нагрузка, представленная ПАРОЙ СИЛ (моментом)

Парой сил называем систему двух сил, равных по модулю, параллельных и противоположно-направленных сил P₁ и P₂ (рис. 11).

Две параллельные силы образуют плоскость. Проведем кратчайшее расстояние между этими силами (перпендикуляр к ним). Отрезок А - В назовем d – плечом одной силы по отношению к другой.

Эта пара сил, имеющая противоположное направление, создает вращение – мы говорим момент. Величина момента пары сил определяется произведением модуля (величины) одной из сил на плечо между этими силами

размерность момента – сила, умноженная на единицу длины, т.е. или .

Направление момента определяется направлением вращения силы P₁ относительно точки В или направлением вращения силы P₂ относительно точки А (рис. 11).

На конструкцию момент прикладывается к какой-нибудь точке (В) с указанием направления вращения и его величины (рис. 12).

Момент пары сил характеризуется и вектором момента, который будет направлен перпендикулярно к плоскости действия пары сил (рис. 13) и приложен в точке С, расположенной на середине плеча d. Положительное направление вектора момента принято такое, когда мы смотрим навстречу его направления и видим вращение против часовой стрелки – правило винта (буравчика).

Говоря о моменте, нужно осветить еще 2 вопроса:

момент силы относительно точки и момент силы относительно оси.

Момент силы относительно точки «О» (рис. 14).

Возьмем силу Р и точку О. Прямая и точка, не лежащая на этой прямой, образуют плоскость. Вектор момента примет вид: , где d – перпендикуляр, опущенный из точки О на линию действия силы. Частные случаи:

а) M_о = 0, если d = 0, а это возможно в том случае, если сила P проходит через точку О;

в) M_о не изменит своей величины, если сила P будет перемещаться по ее линии действия (рис. 15).

Из векторной алгебры известно: но из прямоугольного треугольника ОАВ катет ОВ = d находится ; из

треугольника ОСВ катет ОВ = d находится и т.д., т. е. , где бы сила P по линии ее действия ни была.

Момент силы относительно оси

Возьмем силу P в пространстве и ось (скажем) z (рис. 16). На оси z наметим произвольную точку О. Через точку О проведем плоскость Г (гамма), перпендикулярную оси z. Спроецируем силу P на плоскость Г (гамму). Тогда

Момент силы относительно оси равен нулю в двух случаях:

P_z= 0. В этом случае сила P // оси z (рис. 17).
d = 0. В этом случае сила P проходит через ось z (пересекает ось), т. е. сила и ось находятся в одной плоскости (рис. 18).

РАВНОДЕЙСТВУЮЩАЯ СИЛ

В расчетах важное место отводится вопросу нахождения равнодействующей системы сил и равновесия системы.

Равнодействующая – одна сила, заменяющая действие всех сил, приложенных на тело (конструкцию).

Способы определения равнодействующей.

1. Плоская система сходящихся сил.

Графический способ нахождения равнодействующей.

В основе нахождения равнодействующей cходящейся системы сил лежит аксиома «параллелограмма сил» теоретической механики, согласно которой равнодействующая R двух сил представляет собой диагональ, соединяющую точки А и В параллелограмма, построенного на сторонах сил F₁и F ₂ (рис. 19 –

он построен по принципу: из конца силы F₁ проводим прямую параллельно силе F₂, а из конца силы F₂ проводим прямую параллельно силе F₁. Пересечение этих прямых определяет точку В).

Из рисунка 19 видно, что отрезок СВ равен величине силы F₂. Тогда равнодействующую двух сил можно найти по так называемому силовому треугольнику (рис. 20), который строится по следующему принципу: из произвольной точки А на чертеже проводим отрезок АС, равный по величине и параллельный силе F₁, из точки С проводим отрезок СВ, равный по величине и параллельный силе F₂. Тогда равнодействующая R этих сил будет отрезок АВ. Геометрическая запись равнодействующей примет вид: R = F₁ + F₂.

Рассмотрим несколько сил: F₁, F₂, F₃, F₄ (рис. 21).

Найдем равнодействующую R₁ сил F₁ и F₂. (R₁=F₁+F₂). Затем найдем равнодействующую R₂ = R₁ + F₃ и т.д.

Равнодействующая R₃ и является равнодействующей сил F₁_, F₂, F₃, F₄, т.е.

R₃ = F₁ +F₂+F₃+F₄.

Аналитический способ определения равнодействующей.

Аналитический способ предусматривает наличие координатных осей (или осей заданного направления) и разложения вектора–силы на эти оси (или по проекциям вектора-силы восстановить сам вектор-силу).

Дан вектор - силы – F (рис.22 а). Найти его проекции на координатные оси.

Проекция вектора на ось х есть алгебраическая величина , равная произведению модуля силы на косинус угла между направлением силы и положительным направлением оси х, т.е.

Процесс проецирования силы на ось х производится по схеме: из начала (А) и конца (В) вектора-силы проводим прямые, перпендикулярные к оси х. Полученный таким образом отрезок АВ и есть .

Проекция силы положительна, если она совпадает с положительным направлением оси х. Проекция силы может быть и отрицательной (рис. 22б), и равной нулю (Cos = 0) (рис. 22в).

Аналогично вектор-силу F можем спроецировать и на ось y (рис. 23).

1. Система сходящихся сил (рис. 24).

Построим для нее силовой многоугольник (рис.25). R – равнодействующая. Поместим многоугольник в систему координат и каждую силу спроецируем на оси х и y. Спроецируем и их равнодействующую - R. Тогда

или ;

аналогично

или .

Вывод: проекция равнодействующей на координатные оси равна сумме проекций ее составляющих на эти оси.

Если даны проекции вектора-силы на координатные оси, то можно построить и определить вектор-силу. Нужно только воспользоваться обратными построениями.

2. Плоская система параллельных сил.

Рассмотрим плоскую систему параллельных сил (рис. 26, для примера взято четыре силы). Величина равнодействующей этих сил есть алгебраическая сумма их величин:

R = F₁+ F₂ + F₃+ F₄ .

Для определения места ее нахождения проведем координатные оси и зафиксируем положение сил относительно оси у. Возьмем алгебраическую сумму (обозначим ее буквой S) каждой силы на расстояние ее от точки О (начало координат), т.е.

S = a*F₁+ b*F₂ + c*F₃ - d*F₄

и приравняем ее величину произведению равнодействующей этих сил R на пока неизвестное расстояние от равнодействующей до точки О – расстояние х.

S = R*x.

Из этого выражения находим : х = S/R или

Числовой пример.

Для системы сил (рис. 27) определить величину и место расположения равнодействующей.

Решение.

R = 10-5+6 = 11 (кН),

S = 10*2 – 5*4 + 6*7 = 42 (кН*м),

х = 42/11 = 3,82 (м).

3. Распределенная нагрузка.

Равнодействующая распределенной нагрузки, меняющейся произвольно q(x) по длине балки (рис. 28), равна в пределе площади фигуры, т. е.

и приложена она в центре тяжести этой фигуры.

Для нахождения равнодействующей на практике участок L разбиваем на несколько равных (или не равных) участков (рис. 29). На участках «a» считаем интенсивность q(х) постоянной и получаем систему параллельных сил, что позволяет свести расчет к уже рассмотренному ранее случаю (рис. 26).

Для равномерно-распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки (q) на длину участка ее действия, т.е. . Равнодействующая прикладывается в центр тяжести прямоугольника (рис. 30).

Для распределенной нагрузки по закону треугольника (рис. 31) равнодействующая равна площади треугольника и приложена в центр тяжести треугольника:

4. Плоская произвольная система сил.

Поместим систему сил в систему координат (рис. 32а). Величину равнодействующей определим по силовому многоугольнику (рис.32б). Точку же приложения равнодействующей определим из условия:

где: - алгебраическая сумма произведений силы на перпендикуляр, опущенный из этой точки О (начало координат) на линию действия силы;

- алгебраическая сумма сил (равнодействующая сил).

Зная величину r , строим этим радиусом окружность с центром О и к полученной окружности проводим касательную параллельно найденной равнодействующей R из силового многоугольника (рис. 32б).

1.3 Условия равновесия конструкции.

Условия равновесия плоской системы сил.

Здания и сооружения, несущие нагрузки, находятся в равновесии. В противном случае здания и сооружения разрушаются.

Расчеты зданий и сооружений основаны на принципе равновесия. Каковы же эти принципы (условия)?

Рассмотрим простой пример. Шар находится на идеально гладкой плоскости (рис. 33). К нему приложены две силы, равные по величине и противоположно направленные, линии действия которых проходят через центр шара. В этом положении шар будет неподвижен – он находится в равновесии.

Найдем равнодействующую этих двух сил:

R = P – P = 0.

Равнодействующая сил равна нулю – это и есть основное условие равновесия.

Для сходящейся системы сил оно выражается в том, что силовой многоугольник замкнутый, т.е. конец последней силы (F5) совпадает с началом

первой силы (F1) (рис. 34).

Из аналитического выражения равнодействующей (рис. 35) следует:

но это возможно, когда R_x= R_y= 0.

Здесь Rx , Ry - проекции равнодействующей на координатные оси практически для всех систем сил.

Если учесть, что Rx и Ry представляют собой сумму всех сил, действующих на конструкцию, то условие равновесия запишется:

;

Для системы параллельных и произвольных сил для нахождения точки приложения равнодействующей использовалось условие:

где: левая часть уравнения есть сумма моментов всех сил, действующих на конструкцию, относительно произвольной точки i, а R*x – момент от равнодействующей, которая в равновесной конструкции равна нулю.

Отсюда мы получили еще одно обязательное уравнение, удовлетворяющее условию равновесия:

Подводя итоги, можно сказать, если конструкция находится в равновесии, то для нее справедливы следующие уравнения статического равновесия:

;

Рассмотрим ряд примеров.

1. Плоская система сходящихся сил, в которой две силы требуется определить, чтобы система была уравновешенной (рис. 36а).

Обозначим неизвестные силы через N₁ и N₂ и направим их от точки пересечения А. Поместим начало координат в точку А. Сила N₁ c осью х составит угол , а сила N₂ – угол .

Запишем уравнения равновесия (для плоской задачи):

, .

Решая совместно два уравнения с двумя неизвестными (N₁ и N₂), найдем:

Следует заметить, что N₁ получили со знаком минус, что означает – направление, нами выбранное, от узла А ошибочно; усилие N₁ будет направлено в точку пересечения сил – точку А (рис. 36 б), только в этом случае система будет в равновесии.

2. Для системы сил (рис. 37) определим неизвестные силы – Н, Р₁, Р₂, которые и обеспечат равновесие системы (конструкции). Уравнения равновесия запишутся в виде:

1. , H - 5Cos = 0. Откуда H = 5 Cos ;

2. , -10 – 5 –5Sin + P₁ + P₂ =0;

3. , 10*а – в*Р₁ + 5*с – d*P₂ + 5*d*Sin =0.

Третье уравнение можем записать в более удобном для решения задачи виде:

3. , 10*(d-a) + 5(d-c) – P₁*(d-b) = 0.

В это уравнение не вошли силы Н, Р₂, 5 кН, поскольку они проходят через точку В (пересекают ее). Нетрудно видеть, что из последнего уравнения находим Р₁: