9 Идентификация законов распределения случайных величин
Идентификация законов распределения случайных величин осуществляется на основе собранной статистической информации, представленной в таблице 8.1. На основе полученной репрезентативной выборки необходимо сделать предположение о законе распределения исследуемой случайной величины, рассчитать его основные параметры и проверить выдвинутую гипотезу о виде закона распределения с помощью критерия согласия Пирсона χ2 (хи-квадрат).
Рассмотрение начнем со случайной величины СВ9 – количество доп. удаленных подключений после тел. консультации. СВ9 – это непрерывная случайная величина. Проверка статистической гипотезы осуществляется с использованием электронной таблицы Microsoft Excel. Статистические данные о количестве оформленных заявок на потребительский кредит рассматриваются за 100 дней, т.е. произведена выборка объемом n=100. Преобразуем эту выборку в интервальный ряд, рассчитаем частоты попадания данной случайной величины в полученные интервалы и определим числовые характеристики эмпирического распределения.
В качестве первого приближения разбиения имеющейся выборки на интервалы будем использовать формулу Стерджесса:
,
где n – число единиц
совокупности; S – число интервалов. В
нашем случае
,
т. е. принимаем число интервалов S = 8.
Длина интервала:
Числовые характеристики эмпирического распределения представлены в таблице 9.1.
Таблица 9.1
Эмпирическое распределение СВ3 – количество доп. удаленных подключений после тел. консультации его числовые характеристики
№ |
Начало интервала, xi |
Конец интервала, xi+1 |
Частота, Mi |
Частость, Wi |
Центр интервала, Xi ср |
Средн. Выб., Mi*Xi ср |
Отклон-е от среднего, (Xi -Xв) |
Квадрат отклон-я, (Xi -Xв)2 |
(Xi-Xв)2*Mi |
1 |
0,000 |
1,125 |
5 |
0,05 |
0,56 |
2,81 |
-4,33 |
18,76 |
93,80 |
2 |
1,125 |
2,250 |
8 |
0,08 |
1,69 |
13,50 |
-3,21 |
10,28 |
82,24 |
3 |
2,250 |
3,375 |
12 |
0,12 |
2,81 |
33,75 |
-2,08 |
4,33 |
51,98 |
4 |
3,375 |
4,500 |
16 |
0,16 |
3,94 |
63,00 |
-0,96 |
0,91 |
14,63 |
5 |
4,500 |
5,625 |
20 |
0,20 |
5,06 |
101,25 |
0,17 |
0,03 |
0,57 |
6 |
5,625 |
6,750 |
18 |
0,18 |
6,19 |
111,38 |
1,29 |
1,67 |
30,13 |
7 |
6,750 |
7,875 |
12 |
0,12 |
7,31 |
87,75 |
2,42 |
5,85 |
70,20 |
8 |
7,875 |
9,000 |
9 |
0,09 |
8,44 |
75,94 |
3,54 |
12,56 |
113,02 |
∑ |
|
|
100,00 |
1,00 |
|
489 |
|
|
457 |
Далее построим гистограмму эмпирического распределения случайной величины СВ3 – количества доп. удаленных подключений после тел. консультации по частостям Wi (рисунок 9.1).
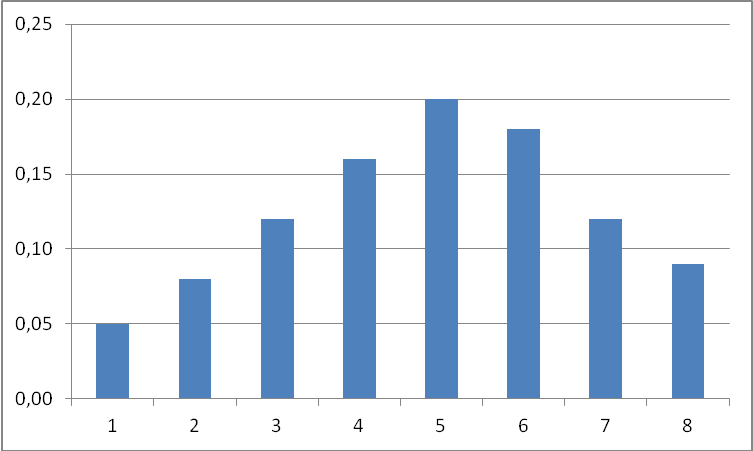
Рисунок 9.1 – Гистограмма эмпирического распределения количество доп. удаленных подключений после тел. консультации
Вид полученной гистограммы позволяет предположить, что исследуемая случайная величина подчиняется нормальному закону.
Выдвигаем гипотезу H0 о том, что расхождение эмпирических и теоретических частот нормального распределения не значимы.
Проверим гипотезу о нормальном распределении генеральной совокупности при уровне значимости α. Для этого:
1) по заданному эмпирическому распределению вычислим выборочную среднюю Xв, выборочное среднее квадратическое отклонение σ, а также среднее арифметическое концов интервалов Xi (см. таблицу 9.1).
Выборочная средняя:
Дисперсия:
,
где S – число интервалов выборочного интервального ряда.
Среднее квадратическое
отклонение (СКО):
2) пронормируем Xi, т.е. перейдем к случайной величине Z, и вычислим концы интервалов по формулам:
и
3) найдем вероятность
попадания случайной величины X в частичный
интервал (Xi, Xi+1) по формуле:
,
где
функция
Лапласа.
Решение пунктов 2 и 3 сведено в таблицу 9.2.
Таблица 9.2
Вычисление теоретических вероятностей попадания в заданный интервал нормально распределенной случайной величины Х1
№ интер-вала |
Xi |
Xi+1 |
Zi |
Zi+1 |
Ф(Zi) |
Ф(Zi+1) |
Pi |
1 |
0,000 |
1,125 |
-2,29 |
-1,76 |
-0,4887 |
-0,4608 |
0,0279 |
2 |
1,125 |
2,250 |
-1,76 |
-1,24 |
-0,4608 |
-0,39251 |
0,06829 |
3 |
2,250 |
3,375 |
-1,24 |
-0,71 |
-0,39251 |
-0,26115 |
0,13136 |
4 |
3,375 |
4,500 |
-0,71 |
-0,18 |
-0,26115 |
-0,07142 |
0,18973 |
5 |
4,500 |
5,625 |
-0,18 |
0,34 |
-0,07142 |
0,13307 |
0,20449 |
6 |
5,625 |
6,750 |
0,34 |
0,87 |
0,13307 |
0,30785 |
0,17478 |
7 |
6,750 |
7,875 |
0,87 |
1,40 |
0,30785 |
0,41924 |
0,11139 |
8 |
7,875 |
9,000 |
1,40 |
1,92 |
0,41924 |
0,47257 |
0,05333 |
4) вычислим теоретические
частоты по формуле:
,
где n – объем выборки (сумма частот).
Вычислим наблюдаемое значение критерия по формуле:
5) сравним эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы K = S-2-1, где S – число интервалов, и сделаем вывод о достоверности гипотезы.
Решение пунктов 4 и 5 представлено в таблице 9.3.
Таблица 9.3
Сравнение эмпирических и теоретических частот
№ интер-вала |
Эмпирическая частота Mi |
Pi |
Теоретическая частота Mi |
(Mi - Mi)2 |
|
1 |
5 |
0,0279 |
2,79 |
4,8841 |
1,7506 |
2 |
8 |
0,06829 |
6,829 |
1,37124 |
0,2008 |
3 |
12 |
0,13136 |
13,136 |
1,2905 |
0,0982 |
4 |
16 |
0,18973 |
18,973 |
8,83873 |
0,4659 |
5 |
20 |
0,20449 |
20,449 |
0,2016 |
0,0099 |
6 |
18 |
0,17478 |
17,478 |
0,27248 |
0,0156 |
7 |
12 |
0,11139 |
11,139 |
0,74132 |
0,0666 |
8 |
9 |
0,05333 |
5,333 |
13,4469 |
2,5214 |
Сумма |
100 |
|
|
|
5,1289 |
Уровень значимости:
Число степеней
свободы:
Используя таблицу
критических точек распределения χ2
Пирсона, по заданному уровню значимости
α и числу степеней свободы K, найдем
критическую точку:
.
Т.к. χ2набл < χ2крит, то делаем вывод о том, что выдвинутая статистическая гипотеза о законе распределения принимается, т.е. случайная величина Х1 - количество оформленных заявок на потребительский кредит подчиняется нормальному закону.
При исследовании законов распределения случайных величин, используемых для создания имитационной модели бизнес-процесса предоставления кредита клиенту, было установлено, что нормальному закону распределения подчиняются следующие случайные величины:
СВ3 - количество отказов клиентам;
СВ4 - количество принятых заявок на телефонные консультации;
СВ5 - количество принятых заявок на удаленное подключение к программе заказчика;
СВ9 - количество доп. удаленных подключений после тел. консультации;
Результаты расчета параметров, характеризующих эти случайные процессы, представлены в таблице 9.4.
Таблица 9.4
Параметры, характеризующие нормальный закон распределения
моделируемых случайных величин
Случайная величина |
Выборочная средняя, Хв |
СКО, σ |
количество оформленных заявок, поступающих в отдел |
2,9826 |
7,01 |
количество отказов клиентам |
2,6309 |
3,77162 |
количество принятых заявок на телефонные консультации |
2,388 |
2,903682 |
количество принятых заявок на удаленное подключение к программе заказчика |
4,9566 |
2,808487 |
количество доп. удаленных подключений после тел. консультации |
5,1289 |
2,13676 |
Рассмотрим случайную величину СВ6 – количество принятых заявок на проведение выезда в офис заказчика. Это непрерывная случайная величина. Проверка статистической гипотезы осуществляется с использованием электронной таблицы Microsoft Excel. Статистические данные о количестве оформленных заявок на потребительский кредит рассматриваются за 100 дней, т.е. произведена выборка объемом n=100. Преобразуем эту выборку в интервальный ряд, рассчитаем частоты попадания данной случайной величины в полученные интервалы и определим числовые характеристики эмпирического распределения.
В качестве первого приближения разбиения имеющейся выборки на интервалы будем использовать формулу Стерджесса:
,
где n – число единиц совокупности; S – число интервалов. В нашем случае , т.е. принимаем число интервалов S = 8.
Длина интервала:
Числовые характеристики эмпирического распределения представлены в таблице 9.5.
Таблица 9.5
Эмпирическое распределение СВ6 – количества принятых заявок на проведение выезда в офис заказчика
№ |
Начало интервала, xi |
Конец интервала, xi+1 |
Частота, Mi |
Частость, Wi |
Центр интервала, Xi ср |
Средн. Выб., Mi*Xi ср |
Отклон-е от среднего, (Xi -Xв) |
Квадрат отклон-я, (Xi -Xв)2 |
(Xi-Xв)2*Mi |
1 |
0 |
0,875 |
29 |
0,29 |
0,4375 |
12,6875 |
-1,82 |
3,3124 |
96,0596 |
2 |
0,875 |
1,75 |
20 |
0,2 |
1,3125 |
26,25 |
-0,945 |
0,89303 |
17,8605 |
3 |
1,75 |
2,625 |
15 |
0,15 |
2,1875 |
32,8125 |
-0,07 |
0,0049 |
0,0735 |
4 |
2,625 |
3,5 |
12 |
0,12 |
3,0625 |
36,75 |
0,805 |
0,64803 |
7,7763 |
5 |
3,5 |
4,375 |
9 |
0,09 |
3,9375 |
35,4375 |
1,68 |
2,8224 |
25,4016 |
6 |
4,375 |
5,25 |
7 |
0,07 |
4,8125 |
33,6875 |
2,555 |
6,52803 |
45,6962 |
7 |
5,25 |
6,125 |
5 |
0,05 |
5,6875 |
28,4375 |
3,43 |
11,7649 |
58,8245 |
8 |
6,125 |
7 |
3 |
0,03 |
6,5625 |
19,6875 |
4,305 |
18,533 |
55,5991 |
∑ |
|
|
100 |
1 |
|
2,2575 |
|
|
3,07291 |
Далее построим гистограмму эмпирического распределения случайной величины СВ6 –количества принятых заявок на проведение выезда в офис заказчика по частостям Wi (рисунок 9.2).
Рисунок 9.2 – Гистограмма эмпирического распределения количества оформленных заявок
Вид полученной гистограммы позволяет предположить, что исследуемая случайная величина подчиняется показательному (экспоненциальному) закону.
Далее выдвигаем гипотезу H0 о том, что расхождение эмпирических и теоретических частот экспоненциального распределения не значимы.
Проверим гипотезу о распределении генеральной совокупности по показательному закону при уровне значимости α. Для этого:
1) по заданному эмпирическому распределению вычислим выборочную среднюю Xв:
Выборочная средняя:
,
где S – число интервалов выборочного интервального ряда
2) примем в качестве оценки параметра λ показательного распределения величину, обратную выборочной средней:
3) найдем вероятность попадания случайной величины X в частичные интервалы (Xi, Xi+1) по формуле:
Решение пункта 3 сведено в таблицу 9.6.
Таблица 9.6
Вычисление теоретических вероятностей попадания в заданный интервал экспоненциально распределенной случайной величины 5
№ интер-вала |
Xi |
Xi+1 |
-λ· Xi |
-λ· Xi+1 |
e-λ· Xi |
e-λ· Xi+1 |
Pi |
1 |
0,000 |
0,875 |
0,000 |
-0,388 |
1,000 |
0,679 |
0,321 |
2 |
0,875 |
1,750 |
-0,388 |
-0,775 |
0,679 |
0,461 |
0,218 |
3 |
1,750 |
2,625 |
-0,775 |
-1,163 |
0,461 |
0,313 |
0,148 |
4 |
2,625 |
3,500 |
-1,163 |
-1,550 |
0,313 |
0,212 |
0,100 |
5 |
3,500 |
4,375 |
-1,550 |
-1,938 |
0,212 |
0,144 |
0,068 |
6 |
4,375 |
5,250 |
-1,938 |
-2,326 |
0,144 |
0,098 |
0,046 |
7 |
5,250 |
6,125 |
-2,326 |
-2,713 |
0,098 |
0,066 |
0,031 |
8 |
6,125 |
7,000 |
-2,713 |
-3,101 |
0,066 |
0,045 |
0,021 |
4) вычислим теоретические частоты по формуле:
, где n – объем выборки (сумма частот).
Вычислим наблюдаемое значение критерия по формуле:
5) сравним эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы K = S-2, где S – общее количество интервалов, и сделаем вывод о достоверности гипотезы.
Решение пунктов 4 и 5 представлено в таблице 9.7.
Таблица 9.7
Сравнение эмпирических и теоретических частот
№ интер-вала |
Эмпирическая частота Mi |
Pi |
Теоретическая частота Mi |
(Mi - Mi)2 |
|
1 |
29 |
0,321 |
32,131 |
9,806 |
0,305 |
2 |
20 |
0,218 |
21,807 |
3,266 |
0,150 |
3 |
15 |
0,148 |
14,800 |
0,040 |
0,003 |
4 |
12 |
0,100 |
10,045 |
3,823 |
0,381 |
5 |
9 |
0,068 |
6,817 |
4,765 |
0,699 |
6 |
7 |
0,046 |
4,627 |
5,632 |
1,217 |
7 |
5 |
0,031 |
3,140 |
3,459 |
1,102 |
8 |
3 |
0,021 |
2,131 |
0,755 |
0,354 |
Сумма |
100 |
|
|
|
4,210 |
Уровень значимости:
Число степеней
свободы:
Используя таблицу
критических точек распределения χ2
Пирсона, по заданному уровню значимости
α и числу степеней свободы K, найдем
критическую точку:
.
Т.к. χ2набл < χ2крит, то делаем вывод о том, что выдвинутая статистическая гипотеза о законе распределения принимается, т.е. случайная величина Х5 - количество заключенных договоров на ипотечное кредитование подчиняется показательному (экспоненциальному) закону.
При исследовании законов распределения случайных величин, используемых для создания имитационной модели бизнес-процесса предоставления кредита клиенту, было установлено, что показательному (экспоненциальному) закону распределения подчиняются следующие случайные величины:
СВ1 – время между поступлениями заявок (мин.)
СВ2 – длительность определения статуса заказчика (мин.)
СВ6 – количество принятых заявок на проведение выезда в офис заказчика;
СВ7 – длительность заполнения журнала заданий (мин.)
СВ8 – длительность телефонной консультации (мин.)
СВ10 – длительность удаленного подключения к программе (мин.)
СВ11- количество доп. выездов в офис к заказчику
СВ12 – длительность консультации у заказчика (час.)
Результаты расчета параметров, характеризующих эти процессы, представлены в таблице 9.8.
Таблица 9.8
Значения параметра λ, характеризующие экспоненциальный закон
распределения случайных величин
Случайная величина |
Значение λ |
время между поступлениями заявок (мин.) |
0,05 |
длительность определения статуса заказчика (мин.) |
0,25 |
количество принятых заявок на проведение выезда в офис заказчика |
0,44 |
длительность заполнения журнала заданий (мин) |
0,21 |
длительность удаленного подключения к программе (мин.) |
0,05 |
количество доп. выездов в офис к заказчику |
0,38 |
длительность консультации у заказчика |
0,25 |
Значения параметра P, характеризующие вероятность наступления события
Случайная величина |
Значение P |
вероятность отказа в предоставлении консультационных услуг |
0,29 |
вероятность необходимости в телефонной консультации |
0,48 |
вероятность необходимости в удаленном подключении |
0,4 |
вероятность необходимости в выезде в офис заказчика |
0,14 |
вероятность необходимости в доп. удаленном подключении |
0,67 |
вероятность необходимости в доп. выезде в офис к заказчику |
0,27 |