
- •Знаходження восьми канонічних форм функції
- •Одержання операторних форм та побудова комбінаційних схем
- •Визначення швидкодії та складності побудованих кс
- •Побудова найоптимальнішої кс з використанням мультиплексора
- •1. Розкладання за змінними x1 та x2
- •2. Розкладання за змінними x1 та x3
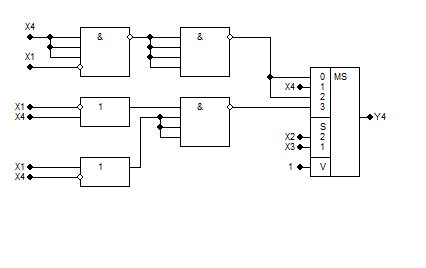
- •3. Розкладання за змінними x1 та x4
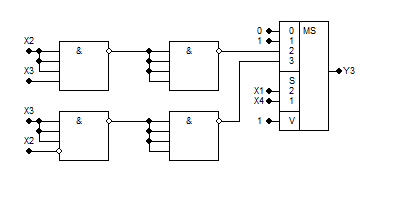
- •4. Розкладання за змінними x2 та x3
- •5. Розкладання за змінними x2 та x4
- •6. Розкладання за змінними x3 та x4
- •Побудова перетворювача кодів з використанням елементів 3і-не та 4-входового дешифратора з інверсними виходами.
3. Розкладання за змінними x1 та x4
X2 ——— |
|
|
|
|
||
F2 |
|
F3 |
|
F2 |
|
|
0 |
|
1 |
1 |
|
1 |
|
0 |
|
0 |
0 |
|
1 |
|X3 |
F0 |
|
F1 |
|
F0 |
||
0 |
|
0 |
1 |
|
0 |
|
1 |
|
1 |
0 |
|
1 |
|





= 40 +
4. Розкладання за змінними x2 та x3
|
F2 |
|
F0 |
||
X1| |
0 |
0 |
|
0 |
0 |
F3 |
|
F1 |
|||
1 |
0 |
|
1 |
0 |
|
|
0 |
1 |
|
1 |
0 |
|
F2 |
|
F0 |
||
|
0 |
1 |
|
1 |
0 |
|
|
—— X4 |
|
||





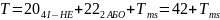
5. Розкладання за змінними x2 та x4
|
F2 |
|
F3 |
|
F1 |
|
F0 |
|
X1| |
0 |
|
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|X3 |
|
|
0 |
|
1 |
|
1 |
|
0 |
|
|
0 |
|
1 |
|
1 |
|
0 |
|
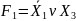


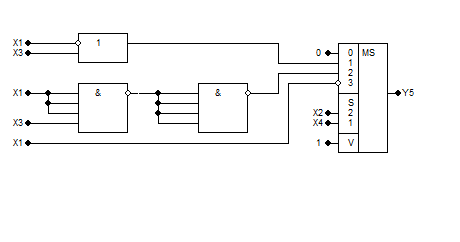


6. Розкладання за змінними x3 та x4
|
X2 ——— |
|
|
|
||
|
F0 |
|
F1 |
|
F0 |
|
X1| |
0 |
|
0 |
0 |
|
0 |
F2 |
|
F3 |
|
F2 |
||
1 |
|
0 |
1 |
|
0 |
|
|
0 |
|
1 |
1 |
|
0 |
|
F0 |
|
F1 |
|
F0 |
|
|
0 |
|
1 |
1 |
|
0 |
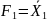
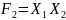

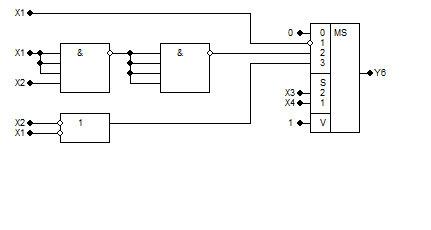
Найоптимальніші КС з використанням мультиплексора – схеми з розкладанням за змінними X2 і X4 та X3 і X4 . Їхня складність N=2.14, швидкодія (час затримки) T = 40 + Tms (нс).
Порівняно зі схемою без використання мультиплексора, дана схема є більш складною. У схеми без мультиплексора N=2, в схеми з мультиплексором – N=2.14
