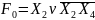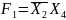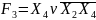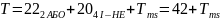Міністерство освіти і науки, молоді та спорту України
Національний технічний університет України
«Київський Політехнічний Інститут»
Факультет прикладної математики
Кафедра спеціалізованих комп’ютерних систем та системного програмування
Лабораторна робота № 1
З дисципліни «Компютерна схемотехніка»
На тему: «Проектування комбінаційних схем»
Виконав:
Студент групи КВ-02
Соляніченко Дмитро Станіславович
Номер залікової книжки: КВ0314
Київ 2012
Завдання для лабораторної роботи
Довизначити перемикальну функцію, задану табл. 1.2. Для цього варіант (дві молодші цифри номера залікової книжки) подати у двійковій системі числення у вигляді слова a6 a5 a4 a3 a2 a1. Значення підставити в табл. 1.2.
1110 -> 001110.
Подати функцію у восьми канонічних формах.
Одержати операторні форми функції, які можна реалізувати на логічних елементах, заданих табл. 1.4 (за варіантом) і побудувати відповідні КС, вважаючи, що на входи КС можуть надходити прямі та інверсні значення змінних.
Для кожної побудованої КС визначити її швидкодію (Т) та складність (N). Усі мікросхеми з табл. 1.4 мають по 14 виводів. Вибрати КС з максимальною швидкодією та мінімальними апаратурними витратами.
Побудувати найоптимальнішу КС для реалізації функції, заданої табл. 1.2, використавши мультиплексор з двома входами керування та логічні елементи з табл. 1.4 (за варіантом). Порівняти складність одержаної схеми зі схемою, побудованою без використання мультиплексора, вважаючи, що два мультиплексори розміщуються в одному корпусі мікросхеми з 16-ма виводами.
Побудувати перетворювач кодів (табл. 1.3), використавши елементи 3І-НЕ та 4-входовий дешифратор з інверсними виходами. Визначити значення складності N беручи до уваги, що дешифратор реалізовано у вигляді мікросхеми на 24 виводи.
Варіант 01: a6 a5 a4 a3 a2 a1 = 001110
Таблиця 1.2 Таблиця 1.3
X1 |
X2 |
X3 |
X4 |
Y |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Таблиця істинності
Входи |
Виходи |
||||||
X1 |
X2 |
X3 |
X4 |
Z1 |
Z2 |
Z3 |
Z4 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
Таблиця 1.4
Таблиця логічних елементів
a3 a2 a1 |
Тип елементів |
Кількість елементів у корпусі мікросхеми |
Час затримки сигналу, t, нс |
1 1 0 |
2АБО-НЕ 3І |
4 3 |
20 24 |
Знаходження восьми канонічних форм функції
Діаграма Вейча заданої функції:
|
X2 —— |
|
|
|
|
X1| |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
|X3 |
|
|
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
1 |
|
|
|
—— X4 |
|
|
|
МДНФ:
Y =
=
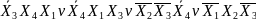v
=
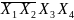(форма І/АБО)
=
=
=
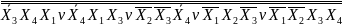= (форма
І-НЕ/І-НЕ)
=
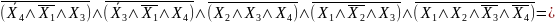= (форма АБО/І-НЕ)
=
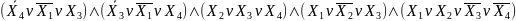(форма
АБО-НЕ/АБО)
МДНФ заперечення функції:
Y̅ =
=
= (форма
І/АБО-НЕ)
=
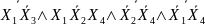= (форма
І-НЕ/І)
=
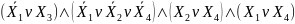= (форма
АБО/І)
=
=
=
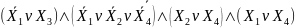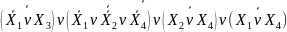(форма АБО-НЕ/АБО-НЕ)
Одержання операторних форм та побудова комбінаційних схем
Наявні елементи 3І та 2АБО/НЕ, тому можна скористатися формами І/АБО-HE і АБО-НЕ/АБО-НЕ.
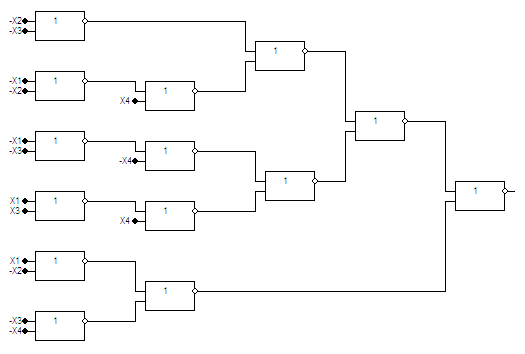
Схема
I/АБО-НЕ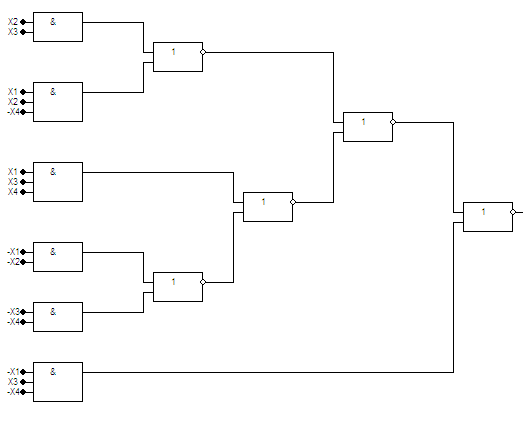
Визначення швидкодії та складності побудованих кс
Для першої схеми:
К = 14
М = 27
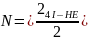
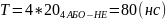
Для другої схеми:
К = 11
М = 25
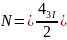
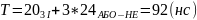
Отже, перша схема більш оптимальна.
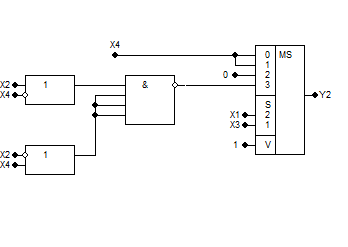
Побудова найоптимальнішої кс з використанням мультиплексора
|
X2 —— |
|
|
|
|
X1| |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
|X3 |
|
|
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
1 |
|
|
|
—— X4 |
|
|
|
1. Розкладання за змінними x1 та x2
F3 |
|
F2 |
|
||
0 |
1 |
|
1 |
1 |
|
0 |
0 |
|
0 |
1 |
|X3 |
F1 |
|
F0 |
|||
0 |
0 |
|
1 |
0 |
|
1 |
1 |
|
0 |
1 |
|
|
—— X4 |
|
|
||
=
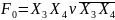
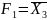
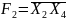
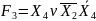
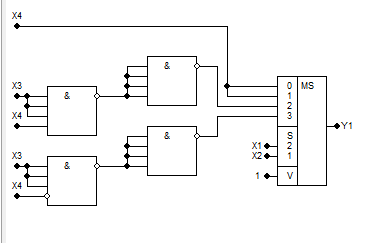
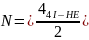
40 +
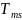
2. Розкладання за змінними x1 та x3
X2 —— |
|
|
|
|
0 |
1 |
1 |
1 |
F2 |
|
|
|
|
|
0 |
0 |
0 |
1 |
F3 |
|
|
|
|
|
0 |
0 |
1 |
0 |
F1 |
|
|
|
|
|
1 |
1 |
0 |
0 |
F0 |
|
—— X4 |
|
|
|
