11 Показатели вариации: общее понятие и использование.

Наряду со средней, как бы она правильно ни была рассчитана, всегда имеются варианты, которые отличаются от средней по величине. Отличие варианты от средней и изучается чтобы определить на сколько надежно средняя дает качественную хар-ку ед. сов-ти.

Показатели вариаций используются очень широко для определения надежности средней, в дисперсионном анализе.

Различают след. показ-ли вариации:

- размах вариации

-ср. линейное отклонение абсолютные показатели

-ср. квадратическое отклонение

- коэфф-т оссиляции

-коэфф-т линейной вариации относительные показатели

-коэфф-т вариации.

Наиболее широко используются ср. линейное отклонение, ср. квадратическое отклонение и коэфф-т вариации.

12 Среднее линейное отклонение: применение и методика расчета.

Среднее линейное отклонение определяется как средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средних арифметических.

Среднее линейное отклонение как мера вариации признака применяется в статистической практике редко, а именно тогда, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется оборот внешней торговли, состав работающих, ритмичность производства и т. д.

1. Для первичного ряда:

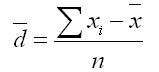
2. Для вариационного ряда:

где сумма n — сумма частот вариационного ряда.

Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор фирмы провести статистический анализ длины черенков. Отобрал 10 штук и замерял их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно в среднем на 16 см. 

13Среднее квадратическое отклонение

Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение (сигма) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: сигма~ 1,25.

Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.