двоичная ПСС характеризуется громоздкостью записью чисел и трудностью их восприятия человеком, восьмеричная и шестнадцатеричная ПСС непосредственно не используются в компьютерах, а служит для облегчения чтения и записи человеком операторам машинных кодов и широко используются в техники программирования.

Очевидно, для человека самой удобной является десятичная ПСС, а для машины двоичный, это вызвало появление некоторой смешанной двоичной - десятичной системы.

Двоичное десятичное число образуется следующим образом: каждая цифра десятичного числа заменятся четырёх разрядным двоичным числом – двоичный тетрадей.

1 9 6 4₍₁₀₎

0001 1001 0110 0100_(2-10)

При обратном преобразовании необходимо заменить эквивалентной её десятичной цифрой.

101 0010 1000_(2-10)

5 2 8

Длинна числа это количество разрядов(позиции) в записи числа, длинна разрядной сетки это термин используемый для определения длинны числа. Длинна разрядной сетки для одного и того же числа в разных ПСС не одинаково: чем меньше основание системы, тем больше длинна разрядной сетки.

Перевод чисел из одной системы счисления в другую. Существует 2 основных перевода чисел из одной СС в другую.

1. Табличный

1011001₍₂₎=Х₍₁₀₎, х₍₁₀₎-?

2⁷2⁶2⁵2⁴2³2¹2⁰

1 0 1 1 0 0 1₍₂₎=1*64+0*32+1*16+1*8+0*4+0*2+1*1=89₍₁₀₎

2. Расчётный - универсален, но применим тока в ПСС

2.1) Перевод целых чисел их десятичной ПСС в любую другую осуществляется методом деления: десятичное число делят на основание новой ПСС до тех пор пока в частном не останется число меньше основания ПСС. Число в новой ПСС запишем в виде остатков отделения начиная с последнего частного представляющего собой старшую цифру числа.

791₍₁₀₎= Х(8),Х(8)-?

791 в тетради!!!!!

2.2) Перевод в правильной десятичной дроби в другую ПСС осуществляется методом умножения : необходимо дробную часть десятичного числа последовательно умножать на основание новой ПСС до тех пор пока в дробной части не останутся нули или не будет достигнута заданная точность перевода. В результате выполнения каждой операции умножения формируется одна цифра нового числа (начиная со старшей) , равное целой части очередного произведения.

0,125(10)=Х(2), Х(2)-?

0.125 в тетради!!!!!!

0.718(10)= Х(8) в тетради!!!2

2.3) Перевод неправильной дроби десятичной ПСС в любую осуществляется в 2 приёма: целая часть переводиться по одному правилу дробная по другому затем целую и дробную части числа записывают вместе отделяя запитой.

Правила преоброзования восьмеричных и шестнадцатиричных чисел в двоичные и наоборот просты так как основания восьмеричной и шестнадцатиричных систем есть целые степени числа 2: 8=2³. 16=2⁴

Для перевода восьмеричного(шестнадцатиричного) числа в двоичную форму достаточно заменить каждую цифру этого числа солтветствующим трехразрядным (4-разрядным) двоичным числом, при этом отбрасывают ненужные нули старшиз разрядов.

5 0 3. 7₍₈₎

101 000 011. 111₍₂₎

F 2 c. 1 A₍₁₆₎

1111 0010 1100. 0001 1010₍₂₎

При переводи из двоичной в восьмеричную (16-ричную) систему поступают следующим образом двигаясь от точки в лева и вправо разбивабт двоичное число на группы по 3(4) разряда дополняя по необходимости нулями крайние левую и правую группы затем группу из трёх(4)разряда заменяют соответствующий восьмеричной (16) цифрой.

11111010101100011.11011₍₂₎, х(8), х(16)-?

011 111 010 101 100 011.110 110

3 7 2 5 4 3 6 6

Правила выполнения арифметических действий над двоичными числами.

Правила выполнения арифметических действий на двочными числами задаются таблицами двоичных сложения вычитания и умножения.

Сложение	Вычитание	Умножение
0+0=0	0-0=0	0*0=0
0+1=1	1-0=1	0*1=0
1+0=1	1-1=0	1*0=0
1+1=1*0(перенос еденицы в старший разряд)	0*-1=1 (заём еденицы из старшего разряда)	1*1=1

При сложении двоичных чисел в каждом разряде производится сложение двух цифр слогаемых или двух этих цифр и еденицы если имеется перенос из соседнего в младшего разряда.

+1101011.01

101110.10

10011001.11

При вычитании двоичных чисел в данном разряде при необходимости занимается еденица из следующего старшего разряда это занимаемая еденица 2-м еденицам данного разряда.

-10001.101

110.011

01011.010

-10111.10

1101.01

Д/з

Умножение двоичных многоразрядных чисел производится путём оброзования частичных произведений и последующего их сумирования. Операция умножения многразрядных двоичных чисел сводится операциям сдвига и сложения. Положение точки определяется также как и при умножении десятичных чисел.

*1011.1

101.01

10111

Операциии деления двоичных чисел выполняется онологично деления 10-ных чисел с учётам таблиц двоичного умножения и вычитания.

1100.011/10.01

Бдагодаря простоте правил двоичной армфметике применение в компьюерах двоичной ПСС позволяет упростить схемы устройств выполняющих арифметических операции.

Естественная форма представления данных.

Структура данных- это перечень и взаимосвязь сведенья необходимых для предсавления данных в разрядной сетке машины.Структура данных для чисел задаётся естественно и нормальными формами.

В естественной форме число записывается с выделением следующих компонентов числа: знака запетой и цифр числа.

Обычно в компьютере положение точки фиксируется схемо-технически – предсавление чисел с фиксированной точкой.

Для дробных чисел обычно точка находится перед старшим разрядом а для целых после младшего.Таким образом сохраняется лишь два структурных компанента поле знака и поле цифр. Достоинство форы представления чисел с фиксированной точкой в том что её применение приводит к значительному упрощению лагически и управляющих схем компьютера. Но при подготовке задач к решению необходимо следить за тем чтобы перед сложением или вычитанием исходные числа имели одинаковые масштабы данных. Кроме того необходимо исключить переполнение разрядной сетки.

Формат данных определяет разрядность размещаемых в разрядной сетке машины структурноых компанентов данных. Для представления чисел с фиксированной точкой используются следующие форматы.

Для представления чисел с фиксированной точкой используется следующие примеры:

Для расширения диапозона представляемых чисел последние могут занимать два-четыре соседних слова.

Нормальные форма предстваления данных.

Для расширения диапозона представления чисел и уменьшения погрешности их задания используется нормальная форма записи.

A=+- MP^+-q

Где м мантиса числа , р основание ПСС , q- порядок числа.

Порядок с учётом знака показывает на сколько разрядов и в какую сторону сдвинута запятая при замене формы записи числа с естественной на нормальную поэтому такую форму записи называют предсталением чисел с плавающей точкой.

В компьютерах используют нармолизованную форму записи для представления чисел с плавающей точкой, число называется нормализованным если его мантиса удовольтворяет условию 1/p<=|m|<1.

При представления в компьютере чисел в форме с плавающей точкой они могут иметь 2 формата: короткий(слово), длинный(двойное слово)-отличается от короткого тока длинной мантисы.

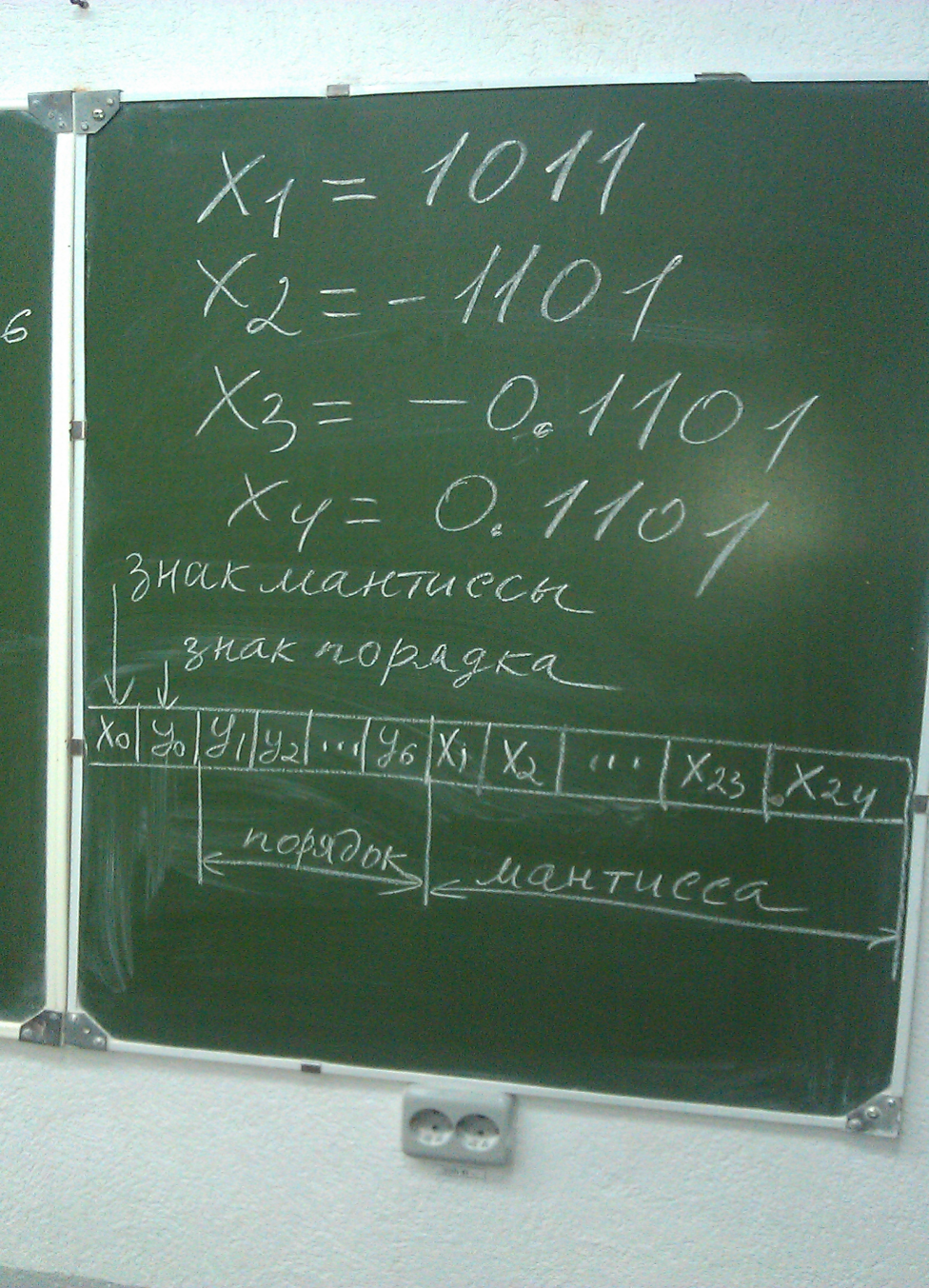
Значение порядка –целое число и определяет положеие точки в числе.Знак продка указывает на пренадлежность числа области целых или дробных чисел.

При представлении чисел в форме с плавающей точкой в компьютере достигается широкий диапозон изображении чиселно структура таких машин значительно усложняется так как необходимо иметь отдельные усторйства для выполнения опираций как над мантиами так и над порядками чиселпри этом скорость выполнения операции ниже что объестняется необходимостью нормализации чисел выравниванию порядка.

Прямой обратный и дополнительные коды.

Для кодировании чисел в компьтере применяют специальные коды:

1. Прямой код

Изображение двоичного числа х в прямом коде основано на представлении его абсолютоного значения закодированного знаком. Таким образом прямой код получается при кодировании в числе только знаковой информации причём +кодируется 0 а – кодируетс 1

Х1=1011

Х2=-11011

Х3=-0.1101

Х4=0.1101

[х1]пр.=01011

[x2]пр.=111011

[x3]пр.=1.1101

[x4]пр.=0.1101

В прямом коде 0 может иметь 2 представления:

0=+0=-0

[+0]пр.=0.0000....0

[-0]пр.=1.0000....0

Код знака числа практически во все компьютерах заносится в каждый разряд разрядной сетке например при использовании 8-ми разрядной сеткой числа:

[x1]пр.=00001011 [x2]пр.=10011011

[х3]пр.=1.1101000

[x4]пр.=0.1101000

Прямой код используется в компьтере для хранения положительных и отрицательных чисел в запоминающих чисел и при выполнении операции умножении.

2. Обратный код числа х обозначается [x]обратное обратный код положительного числа совподает с его прямым кодом, отрицательного числа образуется следующим образом: первое в знаковом разряде записывается 1 , второе в цифровых

В обратном коде возможны 2 представлении 0:

[+0]обр=0.00000....0

[-0]обр=1.111......1

3) Дополнительный код

Дополнительный код числа х обозначается [х]доп. Доп.код с положите.совподает с его прямым кодом.доп.код отрицательного числа образуется следующим образом:1 в знаковом разряде записывается еденица, 2 во все цифровых разрядах заменить еденицы 0 а, 0 еденицами, и третье к младшему разряду числа прибавить еденицу.

[x1]доп= 01011

[x2]доп=100101

[x3]доп=1.0011

[x4]доп=0.1101

В дополнительном коде 0 в машине имеет имеет единственное представление:

[+0]доп=[-0]доп=0.000....0

[-0]доп= 0.0000...0

Обратные и доп. коды позволяют операцию вычитания в компьютере заменить операции сложения что даёт возможность сведения всех арифетических операций к выполнению операции сложения.

Мадифицированные коды.

Иногда в кодах под знак отводятся по 2 разряда такие коды называются модифицирванные (прямым, обратным и дополнительным).

[x1]пр.м.=[x1]обр.м.=[x1]доп.м.=001011

[x2]пр.м.=1111011

[x2]обр.м.=1100100

[x2]доп.м.=1100101

[x3]пр.м.= 11.1101

[x3]обр.м.=11.0010

[x3]доп.м.=11.0011

Сложение двоичных чисел в кодах.

При сложении двоичных чисел в кодах знаковые разряды участвуют в операции сложения на ровне с цифровыми, при этом если выполняется операция сложения в обратных кодах то единица переноса из знакового разряда сумматора прибавляется к её младшему разряду(т.е. выполняется циклический перенос) если же операция сложения выполняется над числами представленными в дополнительным коде то единица переноса из знакового разряда суммы отбрасывается. Переход от обратного и дополнительного кодов прямому выполняется аналогично переходу от прямого кода к обратно

ому и дополнительно соответственно.

При сложении двух чисел с одинаковыми знаковыми знаками возможно переполнение разрядной сетки, это приводит к существенному искажению результата.

Способы обнаружения переполнения:

1. Переполнение отсутствует если имеет место перенос из знакового разряда и в знаковый, либо если они оба отсутствуют.

2. Использование модифицированных кодов : не совпадение знаковых разрядов модифицированного кода является признакам переполнения разрядной сетки: 01 или 10.

Умножение двоичных чисел машинным методом.

Умножение двоичных чисел машинным методом производится по следующим алгоритму:

1. Определяют знак произведения путём сложения по модулю два знаковых разрядов множителей.

2. Перемножение модулей чисел начиная с младшего разряда множителя одним из следующих способов умножения: 1)Множимое неподвижно сумматор частичных произведений сдвигается вправо. 2)Сумматор частичных произведений неподвижен множимое сдвигается влево.

Оба способа дают одинаковый результат, в обоих случаях умножение начинается с анализа младшего разряда множителя. Умножение производится в прямом коде.

1. Способ анализируется очередной разряд множителя: Если он равен 1 то к содержимому сумматора прибавляется множимое и сумматор сдвигается вправо. Если он равен 0 то производится только сдвиг сумматора вправо. Причём количество сдвигов равно количеству разрядов множителя, а количество прибавлений множимого к сумматору равно количеству единиц во множителе.

2. Анализируется второй разряд множителя если он равен единицы то множимое прибавляется в сумме частичных произведений и множимое сдвигается в лево на один разряд. Если он равен 0 то производится только сдвиг множимого влево.

Особенно важным среди циклических является код Грэя. Он строится на базе двоичного по следующему правилу: старший разряд остаётся без изменения; каждый последующий разряд инвертируется если предыдущий разряд исходного двоичного кода равен единице.

Код Грея:

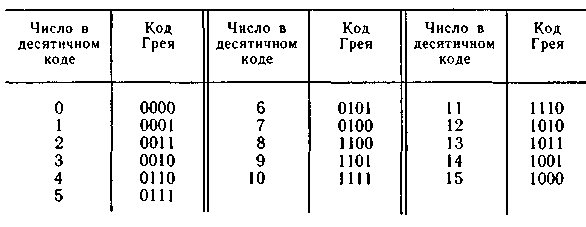
При использовании кода 4221 каждая цифра записывается в виде 4-х разрядной группы. Но её разряды начиная с левого представляют величины 4221. (д.з. сделать таблицу с кодом Грея от 0 до 15 и таблицу с кодами с остатком 3 и 4221 от 0 до 9).

Коды с выявлением ошибок

Общие сведения о кодах с выявлением ошибок

Одним из важнейших аспектов организации хранения и передачи кодов данных является обеспечение их надёжности и без ошибочности применяя специальные методы кодирования можно обеспечить контроль за появлением ошибки и даже восстановление исходного кода после её обнаружения. Применение этих методов позволяет снизить вероятность появления ошибки до 10^-9 и ниже. Общим методом обеспечения надёжности хранения и передачи данных в компьютере и по линиям связи является включение в код дополнительных контрольных разрядов. Существует много различных вариантов этого метода, рассмотрим код с проверкой чётности. При формировании кода слова в контрольный (дополнительный разряд) записывается 0 или 1 таким образом, что бы сумма единиц в слове, включая контрольный разряд, была чётной.

Пример (контроль по чётности 3-х разрядных слов):

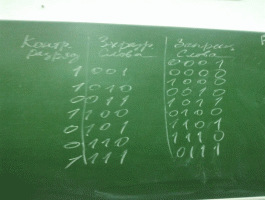
В дальнейшем при всех передачах, слово передаётся вместе со своим контрольным разрядом. Если при передаче информации приёмное устройство обнаруживает, что в принятом слове значение контрольного разряда не соответствует чётности суммы единиц слова, то это воспринимается как признак ошибки. Код контроля по чётности обнаруживает все одиночные ошибки и все случаи не чётного числа ошибок. При одновременном возникновении двух или любого чётного числа ошибок, код с проверкой чётности не обнаруживает ошибок.

Существуют более развитые способы кодирования, которые не только позволяют установить факт появления ошибок большой кратности, но и обеспечивают их исправление. К таким способам относятся коды, принцип построения которых предложил Р. Хемминг.

Рассмотрим общую идею построения кодов Хемминга на следующем примере:

Пусть имеется исходный, 4-х битный код:

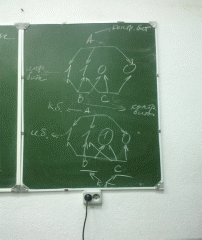
Чтобы не только обнаружить, но и исправить вероятную одиночную ошибку , предлагается каждую тройку битов снабдить одним контрольным разрядом (можно ограничится тремя тройками) количество единиц в каждой группе (тройка битов вместе с контрольным разрядом) должно быть не чётным. На рисунке изображены: исходный код и значения контрольных битов A B C. В каждой выбранной тройке.

Если во время выполнения действий один из битов окажется искажённым, то во всех группах в которые входит ошибочный бит, контроль не чётности покажет наличие ошибки. Следовательно, для определения положения ошибочного вида в коде достаточно выбрать разряд входящий во все группы в которых нарушена не чётность (на рисунке эти биты подчёркнуты). Ошибочный бит должен принадлежать одновременно двум группам. После обнаружения сбойного бита исправление кода осуществляется его инвертирование.

Алгебра логики и теоретические основы синтеза цифровых устройств