3.1. Основы механики горных пород

Механическими свойствами твердого тела являются упругость, пластичность, вязкость, прочность.

В твердых телах основными механическими процессами являются деформирование и разрушение.

Деформирование – процесс изменения размеров или формы твердых тел под влиянием внешних сил. Учитывая гипотезу о сплошности, непрерывное тело до деформирования остается непрерывным и после деформирования, т.е. не имеет разрывов и пустот.

Деформация – это относительное изменение размера или формы тела. Деформации бывают обратимыми и необратимыми. Обратимой называется деформация, при которой прежние форма и размеры тела полностью восстанавливаются после воздействия внешних сил, а необратимой, если не восстанавливаются.

Горные породы имеют ионные и атомные кристаллические структуры.

Элементы структуры связаны между собой кулоновскими силами.

Прочность – это способность твердого тела оказывать сопротивление разрушению от внешнего воздействия.

3.2. Модели твердых тел

Существует несколько методов изучения механических процессов: натурные эксперименты, испытания моделей и теоретический.

В основе теоретического метода лежит математическое моделирование твердого тела, основанное на фундаментальных положениях механики сплошных сред.

Основные модели твердых тел:

• упругое тело или тело Гука (деформируется упруго до разрушения);

• идеальное упругопластическое тело (деформируется упруго до предельных напряжений, далее пластически деформируется при постоянных напряжениях);

• идеальное жестко-пластическое тело или тело Сен-Венана (не деформируется до предельных напряжений, а при равных предельным – происходит пластическая деформация);

• вязкое тело, или тело Ньютона (деформируется подобно вязкой жидкости).

Наибольшее распространение получила модель упругого твердого тела с линейной зависимостью между напряжениями и деформациями.

Напряженное состояние в точке

Напряженное состояние в точке можно описать с компонентами напряжения:

δ_х, δ_у, δ_z, τ_ху, τ_xz, τ_yz,

δ_х, δ_у, δ_z. - нормальные напряжения

τ_ху,τ_xz,τ_yz - касательные напряжения

z

δ_z

τ_хz

τ_yz

τ_zy τ_xz

τ_xy δ_х

δ_х τ_yz

х

y δ_у

Обобщенный закон Гука

Согласно закону Гука деформация прямо пропорциональна нормальному напряжению:

(3.1)

где - деформация растяжения или сжатия;

- нормальное напряжение;

Е – модуль Юнга (модуль деформации при растяжении и сжатии).

μ - коэффициент Пуассона, характеризует упругие свойства тела, связывает деформации по взаимно перпендикулярным направлениям.

γ - деформации сдвига.

, (3.2)

где G – модуль деформации при сдвиге, причем:

(3.3)

Действие внешних сил приводит к изменению не только линейных размеров и форм тела, но и объема.

Объемная деформация пропорциональна среднему напряжению:

(3.4)

где ΔV – изменение объема элементарного куба под действием внешней нагрузки;

V – начальный объем элементарного куба;

К – модуль объемной деформации.

(3.5)

Тогда, обобщенный закон Гука записывается в виде:

(3.6)

(3.7)

Зависимость напряжения от деформации для различных тел:

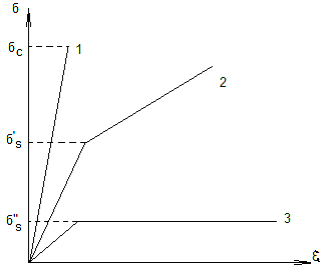
δ_с – предел прочности хрупкого тела,

δ_s' , δ_s" - пределы текучести

Соответственно, зависимости δ от деформации έ различают:

1. хрупкие тела,

2. упрочняющиеся тела,

3. идеально упруго-пластические тела.

Хрупкие (1) деформируются упруго вплоть до разрушения. Упрочняющиеся (2) тела до предела текучести деформируются упруго, а после происходит пластическая деформация. Идеально упруго-пластические (3) до предела текучести также упруго деформируются, затем пластическая деформация увеличивается при постоянном напряжении.

Основными видами разрушений является отрыв и срез.

Отрыв характерен для хрупких тел, пластические деформации незначительны, поверхность разрушения перпендикулярна к напряжению.

Для пластических и упрочняющихся тел характерно разрушение срезом, поверхность разрушения совпадает с плоскостью действия макс. касательных напряжений.

3.3. Условия перехода твердых тел из упругого состояния в пластическое.

Условие Треска-Сен-Венана (Треск – француз. инженер):

Пластическое состояние наступает, когда во всех точках среды макс. касательное напряжение достигает определенного значения:

2 | τ₂ | = |σ₁-σ₃| =σ_s , (3.8)

где σ_s – предел текучести материала при простом растяжении.