Условие Мизеса определяет пластическое состояние в случае, когда удельная упругая энергия изменения формы достигает определенной величины, характерной для материала данного тела

Удельная упругая энергия деформирования:

(3.9)

U можно представить в виде суммы удельных энергий упругого изменения объема U₀ и упругого изменения формы U_ф.

Удельная упругая энергия изменения объема:

(3.10)

Тогда удельная упругая энергия изменения формы:

U_ф=U-U₀ = ½ (σ₁ε₁ + σ₂ε₂ + σ₃ε₃) – 3 (1-2μ) σ₀²/2Е (3.11)

После преобразований получим:

- УСЛОВИЕ МИЗЕСА (3.12)

Условие Мизеса учитывает 3 главных напряжения и в случае 3-осного напряженного состояния дает лучшие результаты, чем условие Треска-Сан-Венана, которое не учитывает σ_2.

3.4. Теории прочности.

Первые исследования, проводимые Леонардо да Винчи и Галилеем привели к созданию первой теории прочности, согласно которой предельное состояние наступает тогда, когда достигает предельного значения одно из главных напряжений:

-σ_n < σ₁ < σ_n ;

-σ_n < σ₂< σ_n ; (3.13)

-σ_n < σ₃ < σ_n ,

где σ_n – предельное напряжение, полученное при одноосном растяжении (+) или сжатии (-).

Вторая теория прочности определяет предельное состояние в случае, когда главная деформация достигает предельного значения.

Запишем через обобщенный закон Гука, используя нормальные напряжения:

-σ_n < σ₁ - μ (σ₂ + σ₃) < σ_n ;

-σ_n < σ₂- μ (σ₁ + σ₃) < σ_n ; (3.14)

-σ_n < σ₃ - μ (σ₁ + σ₂) < σ_n .

Третья теория прочности

При разрушении или достижении пластического состояния значительную роль играют касательные напряжения.

Условие прочности имеет вид:

-τ_n < τ₁ < τ_n;

-τ_n < τ₂ < τ_n; (3.15)

-τ_n < τ₃ < τ_n;

Выразим касательные напряжения через нормальные:

; ; (3.16)

получим:

-σ_n < σ₂ - σ₃ < σ_n;

-σ_n < σ₁ - σ₃ < σ_n; - третья теория прочности (3.17)

-σ_n < σ₁ - σ₂ < σ_n.

Третья теория прочности совпадает с условиями Треска-Сен-Венана. С экспериментальными данными хорошо согласуется при двухосном напряженном состоянии, нашла применение в технике.

Четвертая или энергетическая теория прочности связывает разрушение или достижение пластического состояния с предельным значением удельной энергии формоизменения.

Запишем это условие через главные нормальные напряжения:

2σ²_n ≥ (σ₁ – σ₂)² + (σ₁ - σ₃ ² +(σ₂ - σ₃)² (3.18)

Проведем аналогию с условиями Мизеса.

(3.19)

, (3.20)

По теории прочности U_фп ≥ U_ф. Произведя соответствующие преобразования, можно убедиться, что энергетическая теория прочности совпадает с условием Мизеса. Энергетическая теория носит название Губера-Мизеса-Генки.

Теория прочности Мора определяет зависимость предельного напряжения от среднего напряжения.

τ_n=f(σ_ср), - теория прочности мора, где (3.21)

τ_n- предельное значение касательных напряжений.

; (3.22)

Графически выражением теории прочности Мора является огибающая кругов Мора, построенная по результатам испытаний.

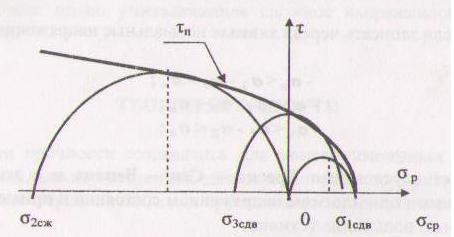
σ_р – предел прочности при растяжении

Недостатком этой теории является то, что не учитывается главное напряжение - σ₂

Обобщенное условие прочности Мора в отличии от теории прочности Мора учитывает все главные напряжения

σ_in=f(σ₀),

где σ_in – предельная интенсивность касательных напряжений, определяемая по формуле:

, (3.23)

где σ₀ – среднее напряжение.

σ₀ = 1/3 (σ₁+ σ₂+ σ₃) (3.24)