
- •Содержание
- •Введение
- •1. Обзор и анализ существующих конструкций
- •2. Описание и принцип действия спроектированного механизма
- •3. Расчёты, подтверждающие работоспособность механизма Расчет и выбор электродвигателя.
- •3.1. Силовой расчёт
- •3.2. Кинематический расчёт
- •3.3.Расчет типовых элементов.
- •3.3.1.Коническая зубчатая пара
- •3.3.2.Реечная передача
- •3.3.3.Выбор и расчет муфты
- •Расчет валов на прочность:
- •Заключение
- •Список использованной литературы
3.1. Силовой расчёт
Крутящий момент на валу двигателя:
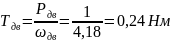
Крутящий момент на валах:
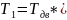 ηзкц*
η2п
= 4.8*0,97*0,992
= 0,23 Нм
ηзкц*
η2п
= 4.8*0,97*0,992
= 0,23 Нм
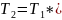 ηзкц*
η2п
= 4.56*0,97*0,992
= 0,21 Нм
ηзкц*
η2п
= 4.56*0,97*0,992
= 0,21 Нм
3.2. Кинематический расчёт
Проанализируем кинематическую схему механизма.
Для преобразования частоты вращения вала двигателя в частоту вращения выходного вала в проектируемом механизме разработан редуктор.
Определим общее передаточное число редуктора
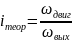
Угловая скорость вращения вала двигателя:
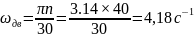
где n –число оборотов двигателя;
Найдём угловую скорость вращения вала:

где
𝜑
–угол
поворота выходного вала,1 °=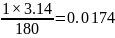 рад;
рад;
t – время, за которое осуществляется поворот.
Отсюда
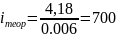
В приборостроении при помощи зубчатой передачи возможно достигнуть максимальное передаточное число на одной ступени равное 8...10.

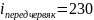
Рассчитаем погрешность редуктора
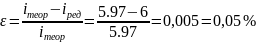
Погрешность не превышает допустимую (2%)
3.3.Расчет типовых элементов.
3.3.1.Коническая зубчатая пара
модуль для зубчатых колес определяется по формуле:
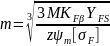
где: М – момент сопротивления
K – коэффициент нагрузки (1,0…1,3)
УFS – коэффициент зависящий от формы зуба (3,5…4,3)
ψm – коэффициент, зависящий от ширины зубчатого венца (1,0…1,2)
[σ] – допускаемое напряжение на изгиб материала
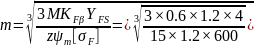
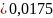 мм
мм
Выбираем из нормального ряда модуль по ГОСТ 9563-60.
m = 0,5 мм.
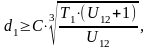
где d1 – делительный диаметр меньшего колеса (шестерни), мм;
С – коэффициент, учитывающий геометрию передачи, и свойства материалов: 2,8 – для стальных незакаленных колес; 2,0 – для стальных закаленных;
Т1 – крутящий момент на валу меньшего колеса, Н∙мм;
U12 – передаточное отношение пары зубчатых колес;


Тогда число зубьев шестерни:

А число зубьев и диаметр колеса:
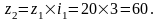

Угол начального конуса для колес:
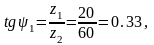
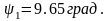
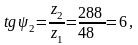
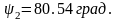
Диаметр окружности выступов (наружный) колес:

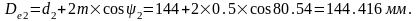
Угол конуса впадин (угол внутреннего конуса):
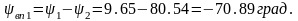

Угол головки зуба:
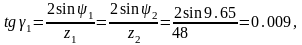
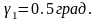
Угол ножки зуба:

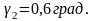
Шаг:
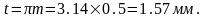
Высота зуба:

Длина зуба:

Длина образующей начального конуса:
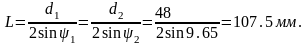
Длина проекции высоты головки зуба на горизонтальную ось:

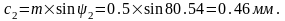
Расстояние от плоскости пересечения начальных конусов до вершины конуса:
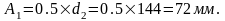
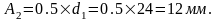
Расстояние от плоскости пересечения конуса до торца (со стороны вершины конуса):

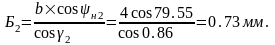
Толщина зуба по хорде делительной окружности:
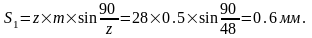
Высота головки зуба от хорды делительной окружности:

3.3.2.Реечная передача
Зубчатое колесо
Выбор материала и термической обработки:
Марка
стали 45, азотирование, предельные размеры
заготовки
 , твердость зубьев в сердцевине 199…240
HB , на поверхности 35…40 HRC,
, твердость зубьев в сердцевине 199…240
HB , на поверхности 35…40 HRC,
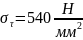
Чем выше твердость рабочей поверхности зубьев, тем выше допускаемые напряжения и тем меньше размеры передачи.
Допускаемые напряжения:
Предварительно определяем среднюю твердость рабочих поверхностей зубьев
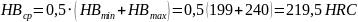
Базовые числа циклов нагружений
При расчете на контактную прочность
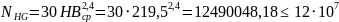
- при расчете на изгиб
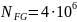
Действительные числа циклов перемены напряжений:
- для колеса
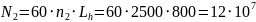
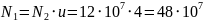
Где
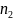 -
частота вращения колеса, мин-1,
-
частота вращения колеса, мин-1,
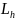 -
время работы передачи ч, u- передаточное
число ступени.
-
время работы передачи ч, u- передаточное
число ступени.
Коэффициент долговечности при расчете по контактным напряжения:

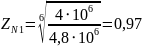

Коэффициент долговечности при работе на изгиб:
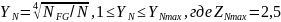
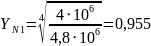

Допускаемые
контактное напряжение
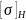 и напряжение изгиба
и напряжение изгиба

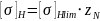

Пределы контактной и изгибной выносливости:
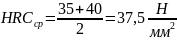
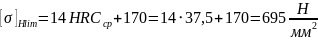

При расчете зубчатых передач цилиндрических в расчетную формулу подставляют при варианте термообработки II допускаемое контактное напряжение.
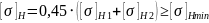
При
выполнении условия для цилиндрических
передач

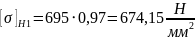

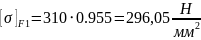
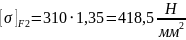
695
d1=228мм=m·z
m=4
z=57
da1=d1+2m=236мм
df1=d1-2.5m=218мм
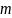 =4
мм
=4
мм
Тип рейки : прямозубая β=0
Угол
наклона зубьев рейки β=10 ,
т.к. β должен быть не более 20
,
т.к. β должен быть не более 20
Высота
головки зуба:
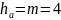 мм.
мм.
Высота
ножки зуба рейки:
 =6
мм.
=6
мм.
Высота
зуба рейки:
 мм.
мм.
Ширина рейки: В=10* =40 мм.
Длина
зуба рейки:
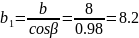 мм.
при длине l=60
мм.
мм.
при длине l=60
мм.
Толщина
зуба:
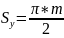 =6,28
мм.
=6,28
мм.

