5.6 Бинарный поиск (метод деления пополам)

Будем предполагать, что имеем упорядоченный по возрастанию массив чисел. Основная идея - выбрать случайно некоторый элемент A_M и сравнить его с аргументом поиска Х. Если A_M=Х, то поиск закончен; если A_M <X, то мы заключаем, что все элементы с индексами, меньшими или равными М, можно исключить из дальнейшего поиска. Аналогично, если A_M >X.

Выбор М совершенно произволен в том смысле, что корректность алгоритма от него не зависит. Однако на его эффективность выбор влияет. Ясно, что наша задача- исключить как можно больше элементов из дальнейшего поиска. Оптимальным решением будет выбор среднего элемента, т.е. середины массива.

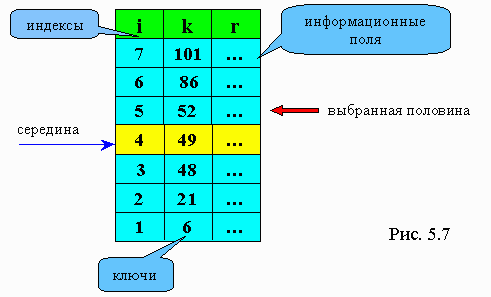
Рассмотрим пример, представленный на рис. 5.7. Допустим нам необходимо найти элемент с ключом 52. Первым сравниваемым элементом будет 49. Так как 49<52, то ищем следующую середину среди элементов, расположенных выше 49. Это число 86. 86>52, поэтому теперь ищем 52 среди элементов, расположенных ниже 86, но выше 49. На следующем шаге обнаруживаем, что очередное значение середины равно 52. Мы нашли элемент в массиве с заданным ключом.

Программы на псевдокоде и Паскале:

Low = 1 hi = n while (low <= hi) do mid = (low + hi) div 2 if key = k(mid) then search = mid return endif if key < k(mid) then hi = mid - 1 else low = mid + 1 endif endwhile search = 0 return

low := 1; hi := n; while (low <= hi) do begin mid := (low + hi) div 2; if key = k[mid] then begin search := mid; exit; end; if key < k[mid] then hi := mid - 1 else low := mid + 1; end; search := 0; exit

При key = 101 запись будет найдена за три сравнения (в последовательном поиске понадобилось бы семь сравнений).

Если С - количество сравнений, а n - число элементов в таблице, то С = log₂n.

Например, n = 1024.

При последовательном поиске С = 512, а при бинарном С = 10.

Можно совместить бинарный и индексно-последовательный поиск (при больших объемах данных), учитывая, что последний также используется при отсортированном массиве.

5.7. Поиск по бинарному дереву

Назначение его в том, чтобы по заданному ключу осуществить поиск узла дерева. Длительность операции зависит от структуры дерева. Действительно, дерево может быть вырождено в однонаправленный список, как правое на рис. 5.8.

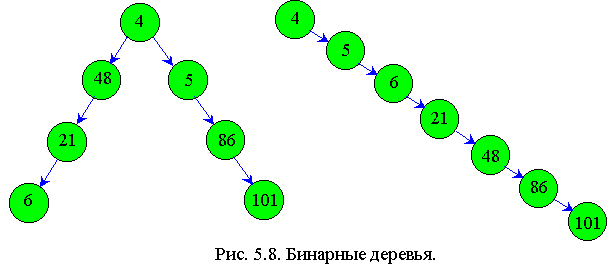
В этом случае время поиска будет такое же, как и в однонаправленном списке, т.е. придется перебирать N/2 элементов.

Наибольшего эффекта использования дерева достигается в том случае, когда дерево сбалансировано.В этом случае для поиска придется перебрать не больше log₂N элементов.

Строго сбалансированное дерево - это дерево, в котором каждый узел имеет левое и правое поддеревья, отличающиеся по уровню не более, чем на единицу.

Поиск элемента в бинарном дереве называется бинарным поиском по дереву.

Такое дерево называют деревом бинарного поиска.

Суть поиска заключается в следующем. Анализируем вершину очередного поддерева. Если ключ меньше информационного поля вершины, то анализируем левое поддерево, больше - правое.

Пусть задан аргумент key

p = tree whlie p <> nil do if key = k(p) then search = p return endif if key < k(p) then p = left(p) else p = right(p) endif endwhile search = nil return

p := tree; whlie p <> nil do begin if key = p^.k then begin search := p; exit; end; if key < p^.k then p := p^.left else p := p^.right; end; search := nil;