5.5.2. Метод транспозиции
В данном методе найденный элемент переставляется на один элемент к голове списка. И если к этому элементу обращаются часто, то, перемещаясь к голове списка, он скоро окажется на первом месте.
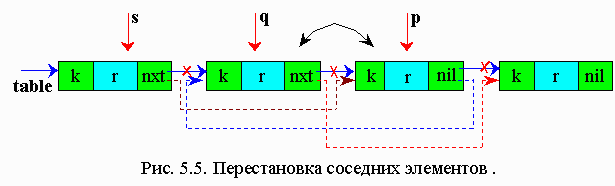
р - рабочий указатель
q - вспомогательный указатель, отстает на один шаг от р
s - вспомогательный указатель, отстает на два шага от q
Алгоритм метода транспозиции:
Псевдокод: s=nil q=nil p=table while (p <> nil) do if key = k(p) then ‘ нашли, транспонируем if q = nil then ‘ переставлять не надо search=p return endif nxt(q)=nxt(p) nxt(p)=q if s = nil then table = p else nxt(s)=p endif search=p return endif endwhile search=nil return |
Паскаль: s:=nil; q:=nil; p:=table; while (p <> nil) do begin if key = p^.k then ‘ нашли, транспонируем begin if q = nil then begin ‘переставлять не на- до search:=p; exit; end; q^.nxt:=p^.nxt; p^.nxt:=q; if s = nil then table := p; else begin s^.nxt := p; end; search:=p; exit; end; end; search:=nil; exit; |
Этот метод удобен при поиске не только в списках, но и в массивах (так как меняются только два стоящих рядом элемента).
5.5.3. Дерево оптимального поиска
Если извлекаемые элементы сформировали некоторое постоянное множество, то может быть выгодным настроить дерево бинарного поиска для большей эффективности последующего поиска.
Рассмотрим деревья бинарного поиска, приведенные на рисунках a и b.Оба дерева содержат три элемента - к1, к2, к3, где к1<к2<к3. Поиск элемента к3 требует двух сравнений для рисунка 5.6 a), и только одного - для рисунка 5.6 б).
Число сравнений ключей, которые необходимо сделать для извлечения некоторой записи, равно уровню этой записи в дереве бинарного поиска плюс 1.
Предположим, что:
p1 - вероятность того, что аргумент поиска key = к1
р2 - вероятность того, что аргумент поиска key = к2
р3 - вероятность того, что аргумент поиска key = к3
q0 - вероятность того, что key < к1
q1 - вероятность того, что к2 > key > к1
q2 - вероятность того, что к3 > key > к2
q3 - вероятность того, что key > к3
C1 - число сравнений в первом дереве рисунка 5.6 a)
C2 - число сравнений во втором дереве рисунка 5.6 б)
Тогда ×р1+×р2+×р3+×q0+×q1+×q2+×q3 = 1
Ожидаемое число сравнений в некотором поиске есть сумма произведений вероятности того, что данный аргумент имеет некоторое заданное значение, на число сравнений, необходимых для извлечения этого значения, где сумма берется по всем возможным значениям аргумента поиска. Поэтому
C1 = 2×р1+1×р2+2×р3+2×q0+2×q1+2×q2+2×q3
C2 = 2×р1+3×р2+1×р3+2×q0+3×q1+3×q2+1×q3
Это ожидаемое число сравнений может быть использовано как некоторая мера того, насколько "хорошо" конкретное дерево бинарного поиска подходит для некоторого данного множества ключей и некоторого заданного множества вероятностей. Так, для вероятностей, приведенных далее слева, дерево из a) является более эффективным, а для вероятностей, приведенных справа, дерево из б) является более эффективным:
P1 = 0.1 P1 = 0.1
P2 = 0.3 P2 = 0.1
P3 = 0.1 P3 = 0.3
q0 = 0.1 q0 = 0.1
q1 = 0.2 q1 = 0.1
q2 = 0.1 q2 = 0.1
q3 = 0.1 q3 = 0.2
C1 = 1.7 C1 = 1.9
C2 = 2.4 C2 = 1.8
Дерево бинарного поиска, которое минимизирует ожидаемое число сравнений некоторого заданного множества ключей и вероятностей, называется оптимальным. Хотя алгоритм создания дерева может быть очень трудоемким, дерево, которое он создает, будет работать эффективно во всех последующих поисках. К сожалению, однако, заранее вероятности аргументов поиска редко известны.