Моделирование поверхности судна
Определение основных элементов проекта
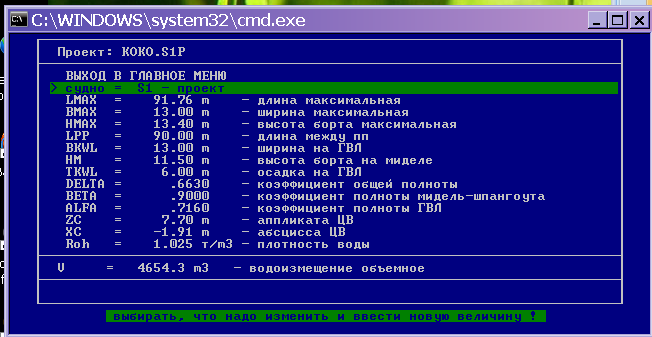
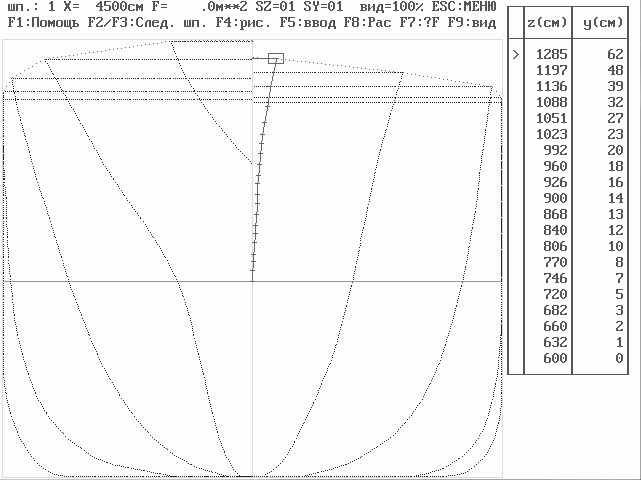
Ввод контуров шпангоутов
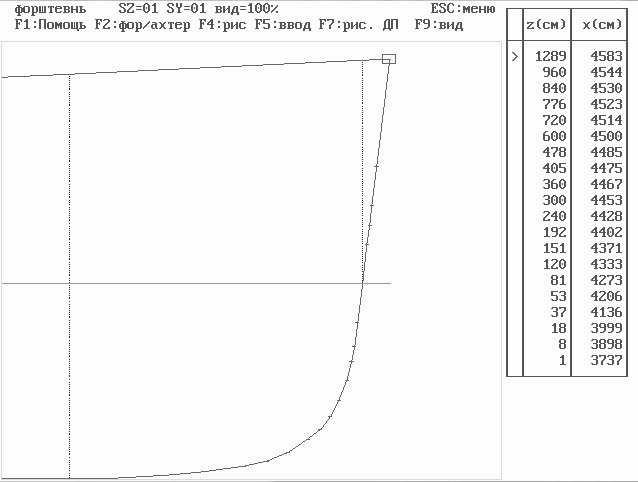
Ввод форштевня
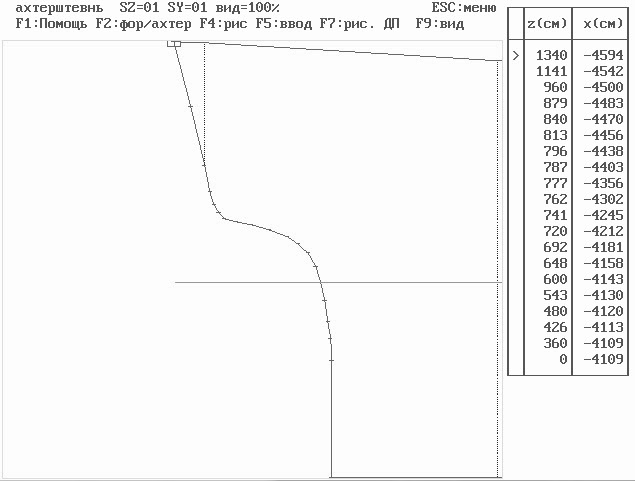
Ввод ахтерштевня
Просмотр всего описания теоретического чертежа
Теоритический расчёт судна
Исчерпывающее представление о форме корпуса судна дает его теоретический чертеж. Он состоит из трех проекций, на каждой из которых изображаются сечения корпуса плоскостями, параллельными рассмотренным выше, - ДП, площадь мидель-шпангоута и ОП. На теоретическом чертеже представляется теоретическая поверхность корпуса без учета наружной обшивки и выступающих частей. Совокупность сечений плоскостями, параллельными ДП, принято называть боком, а сами эти сечения - батоксами. Обычно на этой проекции нос судна изображается справа, а корма - слева. Сечения плоскостями, параллельными пл. мш, наносятся на вторую проекцию, так называемый корпус. В силу симметрии судна относительно ДП на корпусе представляют только половину соответствующего сечения: справа от вертикальной линии - следа ДП - располагают носовые шпангоуты, слева - кормовые, сечение по мидель-шпангоуту помещают полностью, на обеих половинах корпуса. Третья проекция - полуширота - совокупность сечений корпуса плоскостями, параллельными ОП. Здесь также представляются только половины симметричных относительно ДП ватерлиний. Обычно на теоретическом чертеже изображают равноотстоящие батоксы (2-3 на один борт), ватерлинии(10-15) и шпангоуты - 21. Нумеруются батоксы от ДП, ватерлинии - от ОП. Вертикальные линии, проведенные через точки пересечения КВЛ с линиями штевней называются носовым и кормовым перпендикулярами. Для однoвинтoвыx судов кормовой перпендикуляр совпадает с осью баллера руля. Шпангоуту, в плоскости которого лежит носовой перпендикуляр, присваивается номер О, мидель-шпангоуту - номер 1 О, последний, 20-й, номер имеет шпангоут, совпадающий с кормовым перпендикуляром. В отличие от конструктивных шпангоуты на теоретическом чертеже называют теоретическими, а расстояние между ними теоретической шпацией. В районах оконечностей, где форма корпуса изменяется наиболее интенсивно, проводят дополнительные шпангоуты под номерами 1/4, 1/2, 3/4 и 18 1/2, 19 1/2. Все проекции теоретического чертежа должны быть согласованы - они описывают форму одного и того же корпуса. Сечение судна ДП дает представление о палубной и килевой линиях, а также о форме фор- и ахтерштевней. Для морских транспортных судов характерна седловатость (подъем в носу и корме) палубы - это снижает заливаемость оконечностей, особенно при движении на волнении. О форме поперечного сечения палубы и днища, а также соединения их с бортами можно получить представление по сечению пл. мш.
Кривые элементы теоретического чёртежа
Кривые элементов теоретического чертежа представляют собой диаграмму, которая объединяет кривые, определяющие зависимость изменения значений теоретических элементов судна (V, ХC, Z C, Z m, Хf, q 1см, r, R, M1см) от его осадки. Поскольку речь идет об элементах судна, связанных с плавучестью и остойчивостью, т.е. со статикой судна, эту совокупность кривых часто называют кривыми плавучести и начальной остойчивости. Следует заметить, что к элементам теоретического корпуса кроме основных элементов плавучести и элементов остойчивости при малых углах наклонения следует отнести также геометрические характеристики обводов и в первую очередь коэффициенты полноты формы корпуса судна (коэффициент общей полноты δ, коэффициент полноты площади ватерлинии α, коэффициент полноты площади мидель-шпангоута β) поэтому кривые этих элементов также включают и кривые элементов теоретического чертежа. Количество кривых на диаграмме может доходить до 15-20. Для того чтобы определить необходимые значения элементов теоретического чертежа по кривым плавучести и начальной остойчивости, на оси осадок нужно наметить точку, соответствующую заданной осадке, и провести прямую, параллельную оси абсцисс. Отстояние точки пересечения прямой с соответствующей кривой от линии отсчета в выбранном масштабе определяет искомые элементы теоретического чертежа.
Расчёт Кривых элементов теоретического чёртежа
╔════════════════════════════════════════════════════════════╗
║ расчет кривой элементов теоретического чертежа ║
╠════════════════════════════════════════════════════════════╣
║ T - осадка, м ║
║ V - обьёмное водоизмещение, м**3 ║
║ Xc - координаты центра величины, м ║
║ Zc - координаты центра величины, м ║
║ r - поперечный метацентрический радиус, м ║
║ R - продольный метацентрический радиус, м ║
║ Zm - параметр Zm=(4)+(5),м ║
╠═══════╤══════════╤════════╤═══════╤═══════╤═══════╤════════╣
║ T │ V │ Xc │ Zc │ r │ R │ Zm ║
╟───────┼──────────┼────────┼───────┼───────┼───────┼────────╢
║ .10 │ 34.0 │ .00 │ .06 │ 105.4 │ 3816. │ 105.49 ║
║ .68 │ 337.6 │ 2.57 │ .36 │ 16.5 │ 592. │ 16.83 ║
║ 1.25 │ 708.7 │ 2.13 │ .67 │ 9.5 │ 334. │ 10.19 ║
║ 1.83 │ 1113.2 │ 2.07 │ .98 │ 6.8 │ 236. │ 7.80 ║
║ 2.40 │ 1532.0 │ 1.86 │ 1.30 │ 5.4 │ 185. │ 6.66 ║
║ 2.98 │ 1971.0 │ 1.77 │ 1.61 │ 4.4 │ 152. │ 5.97 ║
║ 3.55 │ 2417.0 │ 1.78 │ 1.92 │ 3.7 │ 131. │ 5.62 ║
║ 4.13 │ 2875.7 │ 1.74 │ 2.23 │ 3.2 │ 114. │ 5.43 ║
║ 4.70 │ 3329.3 │ 1.63 │ 2.54 │ 2.8 │ 102. │ 5.37 ║
║ 5.28 │ 3813.3 │ 1.58 │ 2.84 │ 2.5 │ 92. │ 5.37 ║
║ 5.85 │ 4279.1 │ 1.58 │ 3.15 │ 2.3 │ 84. │ 5.45 ║
║ 6.43 │ 4769.9 │ 1.64 │ 3.46 │ 2.1 │ 78. │ 5.56 ║
║ 7.00 │ 5256.4 │ 1.47 │ 3.77 │ 1.9 │ 73. │ 5.71 ║
║ 7.58 │ 5761.6 │ 1.38 │ 4.08 │ 1.8 │ 69. │ 5.88 ║
║ 8.15 │ 6274.3 │ 1.16 │ 4.39 │ 1.7 │ 66. │ 6.08 ║
║ 8.73 │ 6783.2 │ 1.08 │ 4.70 │ 1.6 │ 63. │ 6.30 ║
║
╚═══════╧══════════╧════════╧═══════╧═══════╧═══════╧════════╝
╔════════════════════════════════════════════════════════════╗
║ расчет кривой элементов теоретического чертежа ║
╠════════════════════════════════════════════════════════════╣
║ T - осадка, м ║
║ S - площадь ватерлинии, м**2 ║
║ Xf - координаты ЦТ площади ватерлинии, м ║
║ моменты инерции площади ватерлинии : ║
║ Ix - относительно центральной продольной оси, м**4 ║
║ Iy - относительно оси Y через мидель, м**4 ║
║ If - относительно центральнoй поперечной оси, м**4 ║
╠═══════╤══════════╤════════╤══════════╤══════════╤═════════ ╣
║ T │ S │ Xf │ Ix │ Iy │ If ║
╟───────┼──────────┼────────┼──────────┼──────────┼───────── ╢
║ .10 │ 477.3 │ 2.35 │ .359E+04 │ .130E+06 │ .127E+06 ║
║ .68 │ 613.8 │ 1.70 │ .556E+04 │ .200E+06 │ .198E+06 ║
║ 1.25 │ 677.0 │ 1.66 │ .675E+04 │ .237E+06 │ .235E+06 ║
║ 1.83 │ 718.8 │ 1.58 │ .758E+04 │ .263E+06 │ .261E+06 ║
║ 2.40 │ 749.3 │ 1.56 │ .822E+04 │ .284E+06 │ .282E+06 ║
║ 2.98 │ 769.8 │ 1.55 │ .860E+04 │ .300E+06 │ .298E+06 ║
║ 3.55 │ 788.6 │ 1.53 │ .894E+04 │ .316E+06 │ .314E+06 ║
║ 4.13 │ 802.8 │ 1.50 │ .920E+04 │ .328E+06 │ .326E+06 ║
║ 4.70 │ 815.7 │ 1.46 │ .944E+04 │ .339E+06 │ .338E+06 ║
║ 5.28 │ 827.2 │ 1.40 │ .964E+04 │ .350E+06 │ .348E+06 ║
║ 5.85 │ 838.5 │ 1.32 │ .984E+04 │ .361E+06 │ .359E+06 ║
║ 6.43 │ 849.9 │ 1.19 │ .100E+05 │ .371E+06 │ .370E+06 ║
║ 7.00 │ 861.8 │ 1.03 │ .102E+05 │ .383E+06 │ .382E+06 ║
║ 7.58 │ 874.9 │ .75 │ .104E+05 │ .397E+06 │ .396E+06 ║
║ 8.15 │ 892.6 │ .31 │ .106E+05 │ .415E+06 │ .415E+06 ║
║ 8.73 │ 906.3 │ .05 │ .108E+05 │ .429E+06 │ .429E+06 ║
╚═══════╧══════════╧════════╧══════════╧══════════╧══════════╝
╔════════════════════════════════════════════════════════════╗
║ расчет кривой элементов теоретического чертежа ║
╠════════════════════════════════════════════════════════════╣
║ T - осадка, м ║
║ V - обьёмное водоизмещение, м**3 ║
║ Lwl - длина ватерлинии, м ║
║ Для расчета управляемости судна: ║
║ Sн - площадь носового подреза отн. Lwl, м**2 ║
║ Sк - площадь кормового подреза отн. Lwl, м**2 ║
║ Для расчета сопротивления воды движения судна: ║
║ SF - плошадь смоченной поверхности, м**2 ║
╠═══════╤══════════╤════════╤══════════╤══════════╤══════════╣
║ T │ V │ Lwl │ Sн │ Sк │ SF ║
╟───────┼──────────┼────────┼──────────┼──────────┼──────────╢
║ .10 │ 34.0 │ 80.27 │ .07 │ .00 │ 480.0 ║
║ .68 │ 337.6 │ 83.48 │ 1.04 │ .00 │ 649.9 ║
║ 1.25 │ 708.7 │ 84.48 │ 1.96 │ .00 │ 763.4 ║
║ 1.83 │ 1113.2 │ 85.03 │ 2.78 │ .00 │ 865.8 ║
║ 2.40 │ 1532.0 │ 85.37 │ 3.49 │ .00 │ 963.1 ║
║ 2.98 │ 1971.0 │ 85.60 │ 4.10 │ .00 │ 1057.9 ║
║ 3.55 │ 2417.0 │ 85.74 │ 4.55 │ .00 │ 1152.3 ║
║ 4.13 │ 2875.7 │ 85.87 │ 4.92 │ .01 │ 1245.5 ║
║ 4.70 │ 3329.3 │ 86.01 │ 5.27 │ .02 │ 1338.6 ║
║ 5.28 │ 3813.3 │ 86.18 │ 5.67 │ .07 │ 1431.8 ║
║ 5.85 │ 4279.1 │ 86.37 │ 6.05 │ .13 │ 1525.3 ║
║ 6.43 │ 4769.9 │ 86.60 │ 6.42 │ .28 │ 1677.2 ║
║ 7.00 │ 5256.4 │ 87.00 │ 6.89 │ .73 │ 1778.2 ║
║ 7.58 │ 5761.6 │ 88.07 │ 7.46 │ 2.91 │ 1886.0 ║
║ 8.15 │ 6274.3 │ 89.84 │ 8.08 │ 9.52 │ 2001.1 ║
║ 8.73 │ 6783.2 │ 90.13 │ 8.59 │ 11.12 │ 2104.5 ║