
- •Дифференциальное исчисление глава: производная функция
- •Задача о нахождении скорости движения
- •Определение производной. Ее механический и геометрический смысл.
- •Найти производную функции , где
- •Механический смысл производной
- •Физический смысл производной.
- •Геометрический смысл производной.
- •Связь между непрерывностью и дифференцируемостью
- •Производная суммы, разности, произведения и частного функций
- •Производная сложной функции
- •Практические задачи:
- •Производные основных элементарных функций
- •Производные высших порядков
- •Механический смысл производной второго порядка
- •Дифференциал функции понятие дифференциала
- •Основные теоремы о дифференциалах
- •Дифференциал сложной функции
- •Правила Лопиталя
- •Примеры:
- •Раскрытие неопределенностей различных видов
- •Исследование функций при помощи производных
- •П. Максимум и минимум функций
- •П. Наибольшее и наименьшее значения функции на отрезке
- •Замечания:
- •П. Выпуклость, вогнутость графика функции. Точки перегиба
- •П. Асимптоты графика функции
- •Общая схема исследования функции и построения графика
Примеры:




В этом примере легче без применения правила найти предел, посмотрим

Т.е.
числитель поменялся местом со знаменателем,
но неопределенность сохранилась, и
если применить правило вторично, то
функция под знаком предела примет свой
первоначальный вид. Таким образом,
применение этого правила в данном случае
не позволяет раскрыть неопределенность.
В то же время легко установить, что

 здесь
можно сделать ошибочный вывод, что
предел данной функции не существует,
т.к. не существует
здесь
можно сделать ошибочный вывод, что
предел данной функции не существует,
т.к. не существует
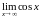 .
.
На
самом деле
 ,
т.к.
,
т.к.
 ,имеем
произведение ограниченной функции
,имеем
произведение ограниченной функции
 и бесконечно малой функции
и бесконечно малой функции
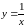 (при
).
(при
).
Раскрытие неопределенностей различных видов
Правило
Лопиталя применяют для раскрытия
неопределенностей
,
,
которые называются основными.
Неопределенности вида
 ,
, ,
,
 ,
,
 ,
,
 сводятся к двум основным видам путем
тождественных преобразований.
сводятся к двум основным видам путем
тождественных преобразований.
Пусть
 при
при
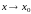 тогда очевидны следующие преобразования
тогда очевидны следующие преобразования
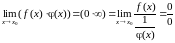 или
или

Пусть
 при
тогда можно поступить так для нахождения
предела
при
тогда можно поступить так для нахождения
предела
 при неопределенности
:
при неопределенности
:

Пусть
 при
(
)
при
(
)
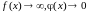 при
(
)
при
(
)
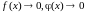 при
(
)
при
(
)
Для
нахождения предела вида
 удобно сначала прологарифмировать
выражение
удобно сначала прологарифмировать
выражение
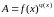 ,
получаем
,
получаем
 ;
;
Откуда
 используя свойство непрерывных функций
используя свойство непрерывных функций
 получаем:
получаем:
Решение можно оформить сразу, подставляя исходные данные в готовую формулу:

Исследование функций при помощи производных
П. ВОЗРАСТАЮЩАЯ, УБЫВАЮЩАЯ ФУНКЦИИ
1
ОПРЕДЕЛЕНИЕ:
Пусть дана функция
 ,
будем говорить, что
возрастающая
функция в точке
,
будем говорить, что
возрастающая
функция в точке
 ,
если при любом достаточно малом
,
если при любом достаточно малом
 ,
выполняется условие
,
выполняется условие
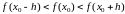 .
.
2
ОПРЕДЕЛЕНИЕ:
Пусть дана функция
,
будем говорить, что
убывающая
функция в точке
,
если при любом достаточно малом
,
выполняется условие
 .
.
3
ОПРЕДЕЛЕНИЕ:
Функция называется возрастающей
в интервале
,
если для любых двух точек
 и
и
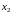 из указанного интервала, удовлетворяющих
неравенству
из указанного интервала, удовлетворяющих
неравенству
 ,
выполняется неравенство
,
выполняется неравенство

4
ОПРЕДЕЛЕНИЕ:
Функция называется убывающей
на интервале
,
если для любых двух точек
и
из указанного интервала, удовлетворяющих
неравенству
,
выполняется неравенство
 .
.
ТЕОРЕМА: (НЕОБХОДИМОЕ УСЛОВИЕ ВОЗРАСТАНИЯ, УБЫВАНИЯ)
Если
дифференцируемая на интервале
функция возрастает (убывает), то
 (
(
 )
для любого
)
для любого
 .
.
Геометрически
теорема означает, что касательные к
графику функции (которая возрастает) и
дифференцируема, образуют острые углы
с положительным направлением оси
 или в некоторых точках параллельны оси
.Положительное
направление задается против часовой
стрелки от
или в некоторых точках параллельны оси
.Положительное
направление задается против часовой
стрелки от
ТЕОРЕМА: (ДОСТАТОЧНОЕ УСЛОВИЕ ВОЗРАСТАНИЯ, УБЫВАНИЯ)
Если
функция
 дифференцируема на интервале
и
дифференцируема на интервале
и
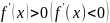 для
любого
,
то эта функция возрастает (убывает) на
интервале
.
для
любого
,
то эта функция возрастает (убывает) на
интервале
.
Данные теоремы довольно просто позволяют исследовать функцию на монотонность.
Функция, возрастающая или убывающая, называются монотонными.
Пример:
Исследовать
функцию на монотонность

РЕШЕНИЕ:
функция определена на
 .
.
 ,
когда
,
когда
 или
или

 или
или


 ,
когда
,
когда
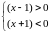 или
или
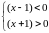 ,
т.е. для всех
,
т.е. для всех

ОТВЕТ: Функция возрастает когда
Функция убывает когда

