Производная суммы, разности, произведения и частного функций

Нахождение производной по определению непосредственно часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.

Пусть даны функции - две дифференцируемые функции в некотором интервале .

ТЕОРЕМА: Производная суммы (разности) двух функций равна сумме разности производных этих функций

ТЕОРЕМА: Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:

Можно показать на основании этой теоремы, что , где ,

.

ТЕОРЕМА: Производная частного двух функци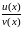й , если , равна дроби, числитель которой есть разность произведений производной числителя на знаменатель дроби и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя:

,

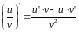Производная сложной функции

Пусть даны и , тогда сложная функция с промежуточным аргументом и независимым аргументом .

ТЕОРЕМА: Если функция имеет производную 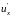в точке , а функция имеет производную в соответствующей точке , то сложная функция имеет производную .

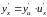ДОКАЗАТЕЛЬСТВО: по условию , отсюда по теореме о связи функции, ее предела и бесконечно малой функции, имеем

;

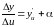или

, где

Аналогично получаем для функции , которая тоже имеет производную в точке , тогда имеем

,

следовательно

или , где

Теперь подставим значение в , получаем:

Разделим на и перейдем к пределу при .

Таким образом, получаем .

ИТАК: Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Это правило остается в силе, если промежуточных аргументов несколько. Так если , , , то .

Практические задачи:

Найти производные функций:

1)

Функция является сложной, найдем ее производную:

Эту функцию можно представить в виде цепочки «простых» функций:

, где , , где 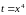, по правилу дифференцирования получаем

2) 3)

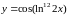
Пользуясь правилом дифференцирования обратной функции, найти производную для функции

, , , ,

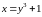Производные основных элементарных функций

САМОСТОЯТЕЛЬНО! Выписать на отдельный лист правила дифференцирования и формулы дифференцирования.

Производные высших порядков

Мы будем говорить о производных высших порядков явно заданной функции , у которой уравнение разрешено относительно .

Мы говорили, что - является также функцией от и называется производной функции 1 порядка.

Если функция - дифференцируема, то ее производная - производная второго порядка.

Обозначения: 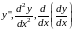. Итак

Производная от если она существует называется производной третьего порядка и обозначается

Производной - го порядка (или -ой производной) называется производная от производной ( ) порядка

Производные порядка выше1-го называются производными высших порядков.

Обозначения начиная с 4 порядка:

--- либо римской цифрой

--- либо обычной цифрой в скобках