Дифференциальное исчисление глава: производная функция

Понятие производной возникло еще в XVIIв., когда формировались основные идеи дифференциального исчисления, задолго до построения строгой теории пределов, которую мы рассматривали в предыдущем семестре. Формирование понятия производной исторически связано с двумя задачами: задачей нахождения скорости движения и задачей проведения касательной к кривой. Рассмотрим одну из этих задач.

1. Задача о нахождении скорости движения

Закон равномерного движения выражается формулой: ,

где -скорость равномерного движения ( является постоянной величиной), - путь, пройденный к моменту времени . Таким образом путь, пройденный в равномерном движении, является линейной функцией от времени. Его график представляет собой прямую линию.

Из выражения , легко получить формулу 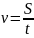, которая показывает, что для нахождения скорости равномерного движения нужно пройденный путь разделить на время.

Однако большинство движений, наблюдающихся в реальной жизни, не могут считаться равномерными. В случае неравномерного движения путь не является линейной функцией от времени, а представляет собой более сложную функцию. Например, закон свободного падения выражается формулой: , где - ускорение свободного падения.

В общем случае путь является функцией от времени. График некоторой функции 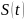(изобразить самим, как на лекции!)

Рассмотрим момент времени и перейдем от него к другому моменту времени .

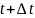К моменту тело прошло путь , к моменту тело прошло путь . Это значит, что за время тело прошло путь . Геометрически представляет собой длину отрезка AB.

Итак, за время от момента до момента тело прошло путь .. Если бы в течение этого времени тело двигалось равномерно, то его скорость, согласно формуле была бы равна Отношение называется средней скоростью в промежутке времени от момента до момента . Средняя скорость не может точно характеризовать быстроту перемещения тела в момент . Если, например, тело в начале промежутка передвигалось очень быстро, а в конце очень медленно, то средняя скорость не отразит этих особенностей движения. Чем меньше промежуток , тем точнее можно охарактеризовать скорость в момент .

Определение: Предел средней скорости движения при стремлении к нулю промежутка времени 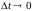называется скоростью движения точки в данный момент времени (или мгновенной скоростью). Обозначив скорость через 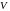, получим:

Определение производной. Ее механический и геометрический смысл.

Пусть функция 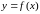определена на некотором интервале .

Проделаем следующие операции:

1) аргументу дадим приращение ,

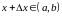
2) найдем соответствующее приращение функции

3) составим отношение приращения функции к приращению аргумента

4) найдем предел этого отношения при .

Если этот предел существует, то его называют производной функции и обозначают

Определение: Производной функции в точке 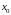называется предел отношения приращения функции к приращению аргумента, когда приращение последнего стремится к нулю

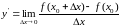
Таким образом, производная функции есть некоторая функция произведенная из данной функции.

ЗАМЕЧАНИЕ: Функция , имеющая производную в каждой точке интервала называется дифференцируемой в этом интервале. Операция нахождения производной функции называется дифференцированием.

Значение производной функции в точке обозначается

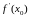
Примеры: