
- •Содержание
- •Предисловие
- •1. Блочные матрицы и операции над ними
- •1.1. Вопросы теории
- •1.2. Примеры решения задач
- •1.3. Примеры для самоконтроля
- •2.1. Вопросы теории
- •2.2. Примеры решения задач
- •2.3. Примеры для самоконтроля
- •3.Жорданова нормальная форма матрицы
- •3.1. Вопросы по теории
- •3.2 Примеры решения задач
- •3.3 Примеры для самоконтроля
- •4.Функции от матриц
- •4.1.Вопросы теории
- •4.2. Примеры решения задач
- •Примеры для самоконтроля
- •5.Матричные уравнения
- •5.1. Вопросы по теории
- •5.2. Примеры решения задач
- •6.Нормы матриц
- •6.1 Вопросы по теории:
- •6.2 Примеры решения задач
- •6.3 Примеры для самоконтроля
- •Функции от матриц
Примеры для самоконтроля
Вычислить функцию от матрицы:
1.
![]() 3
A =
3
A =
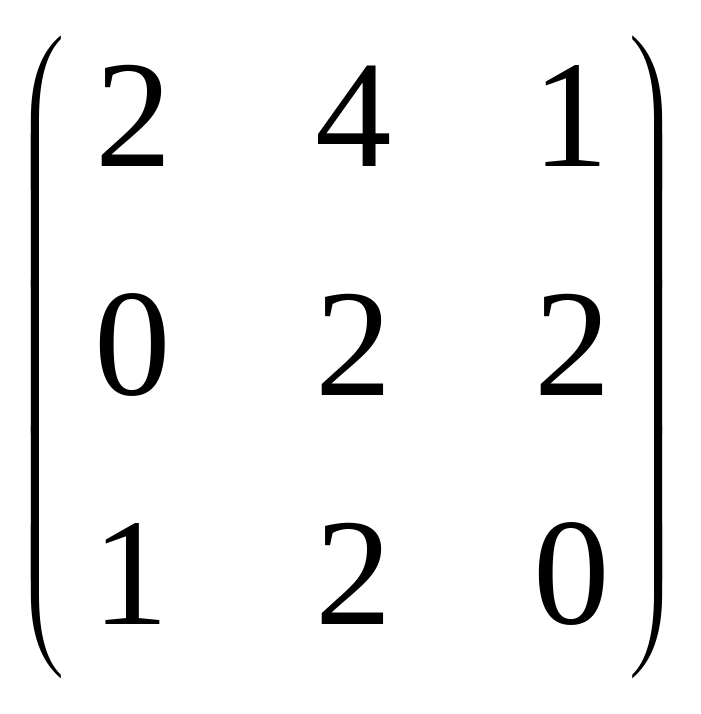
2.
2
A =
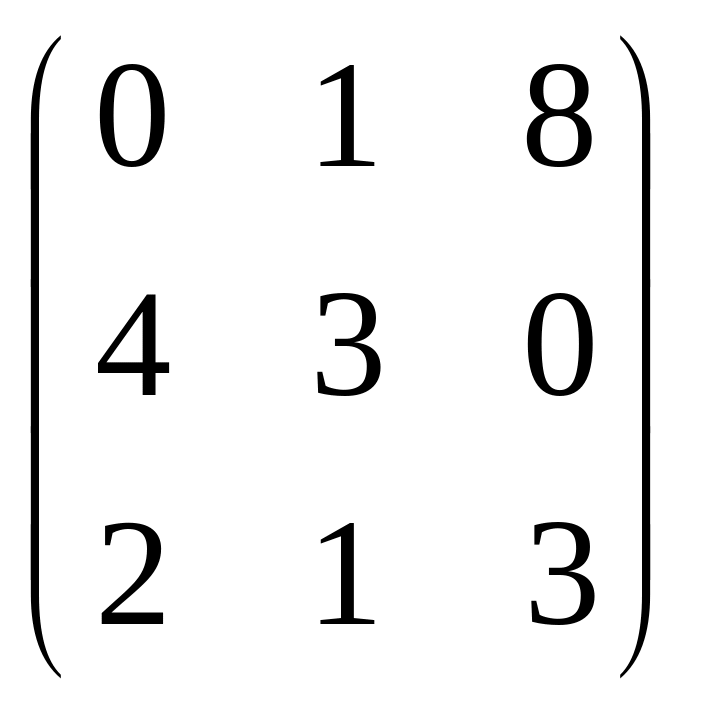
3.
![]() A=
A=
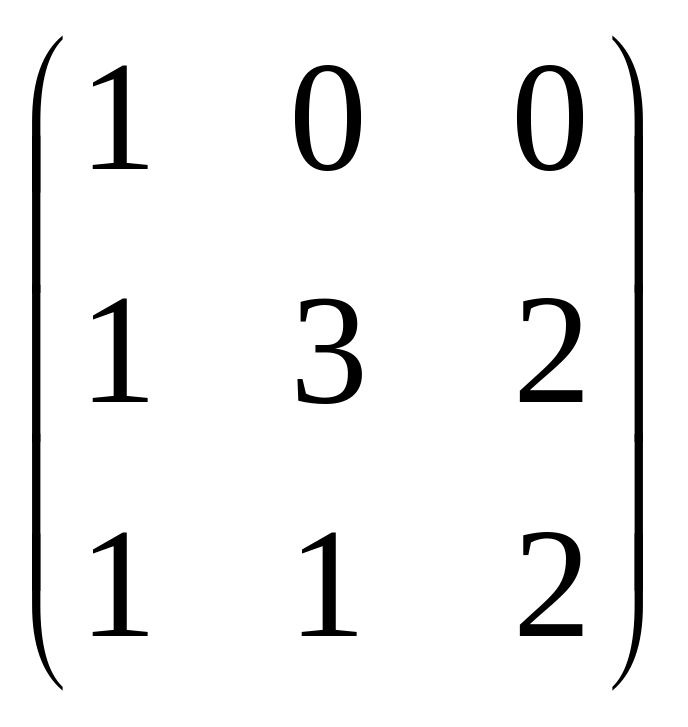
4.
2
A =
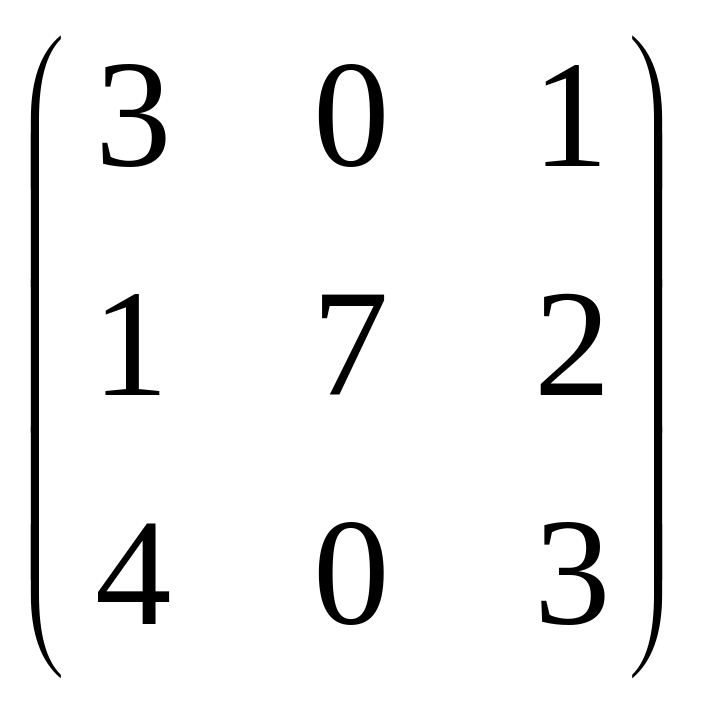
5.
3
A =
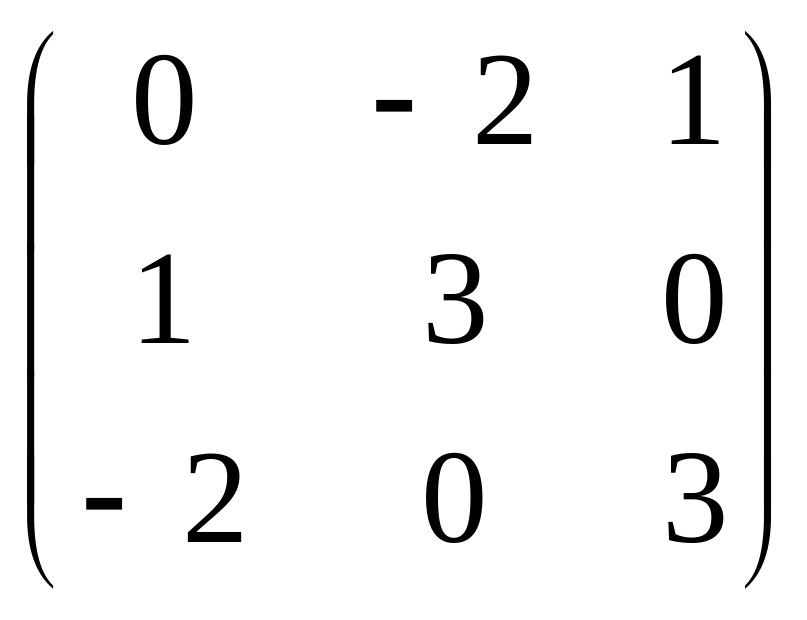
6.
![]() A =
A =
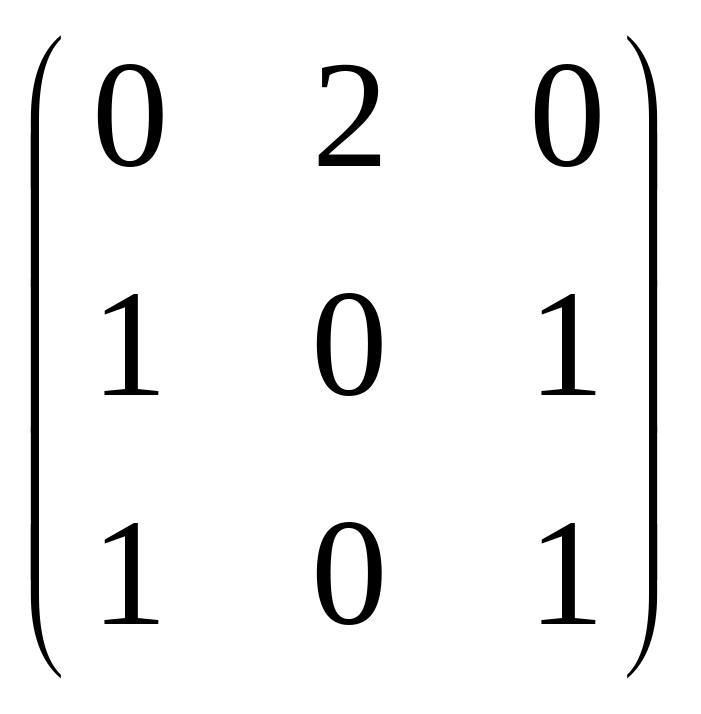
7.
![]() A =
A =
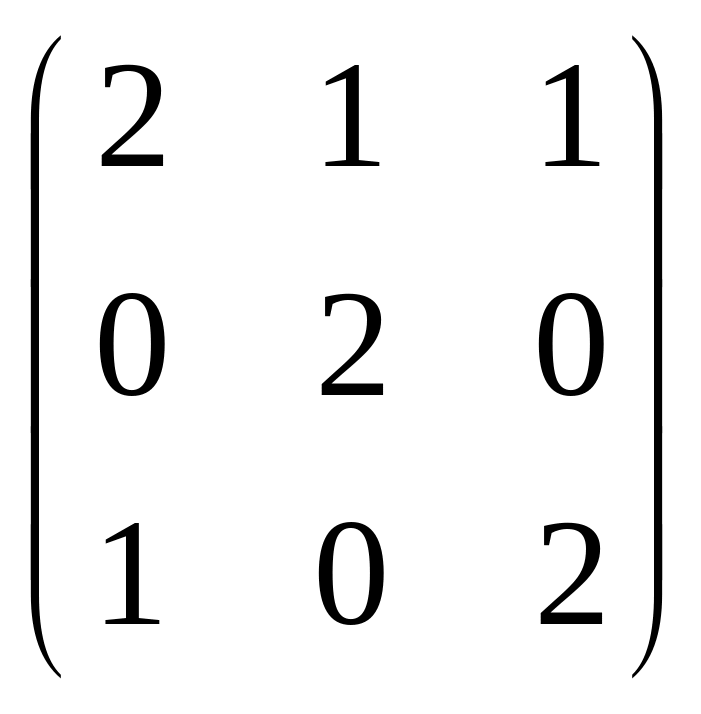
8.
![]() A =
A =
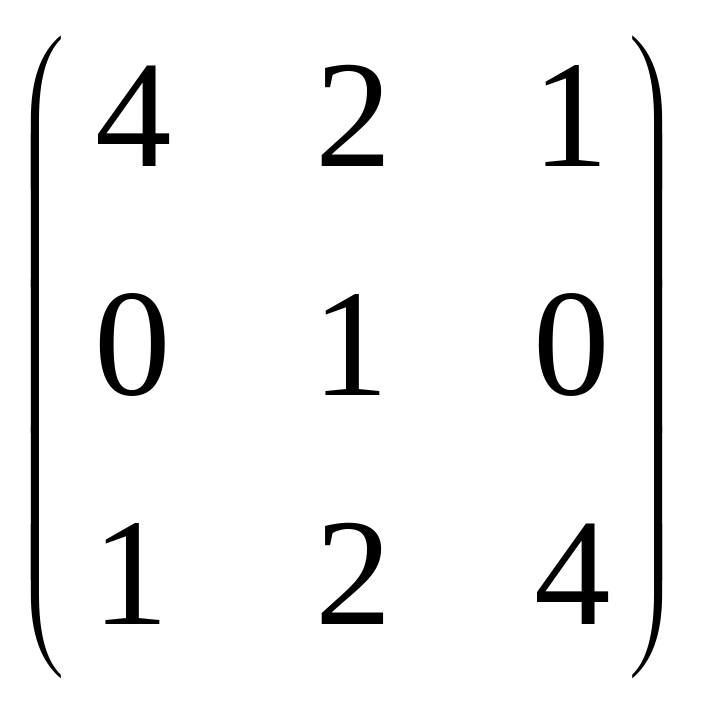
9.
![]() A =
A =

10.
![]() A =
A =
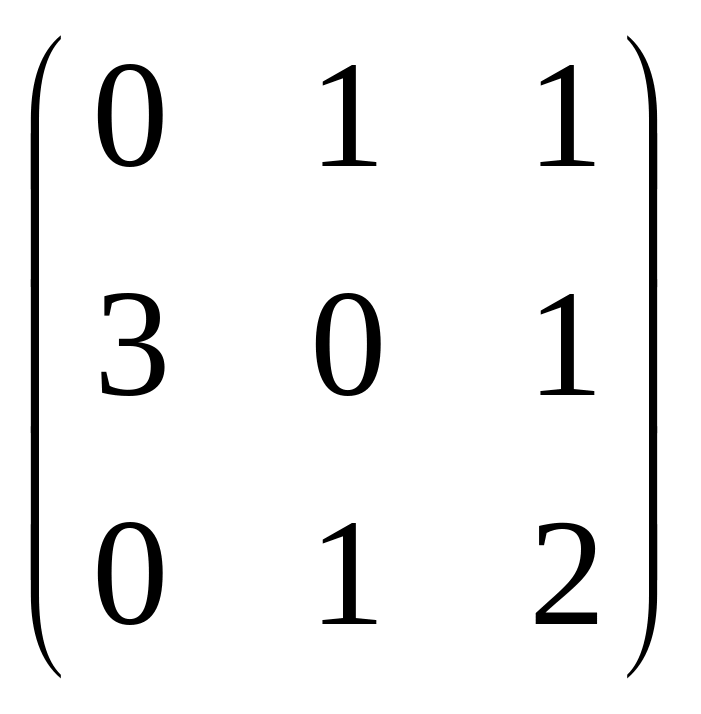
11.
![]() A =
A =
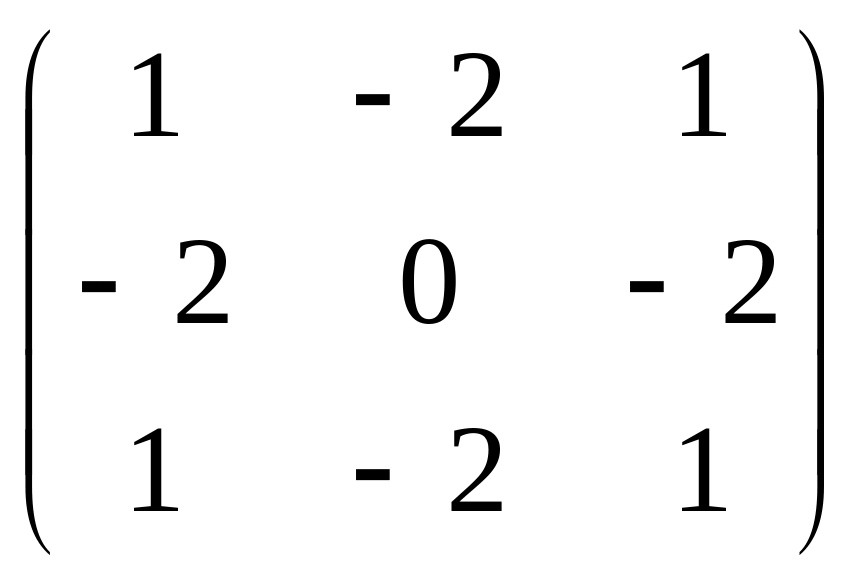
12.
![]() A =
A =
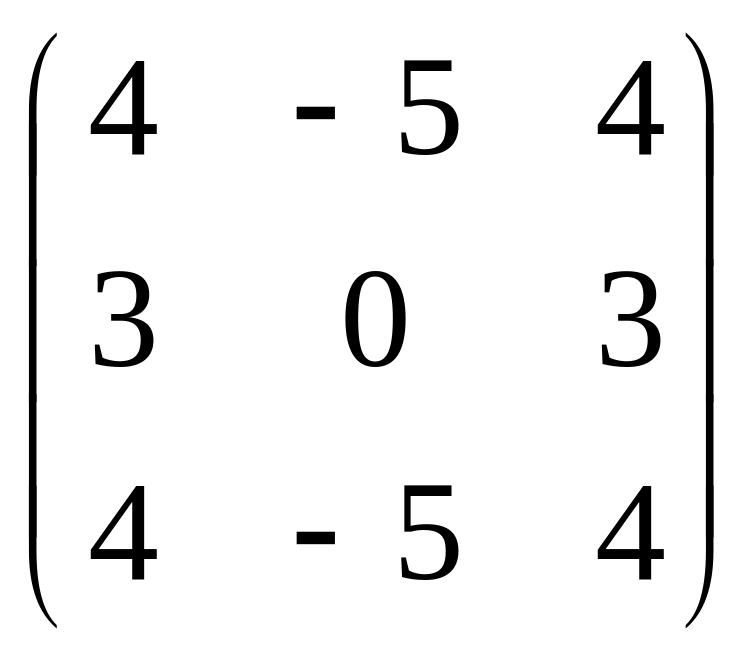
13.
![]() 2
А =
2
А =
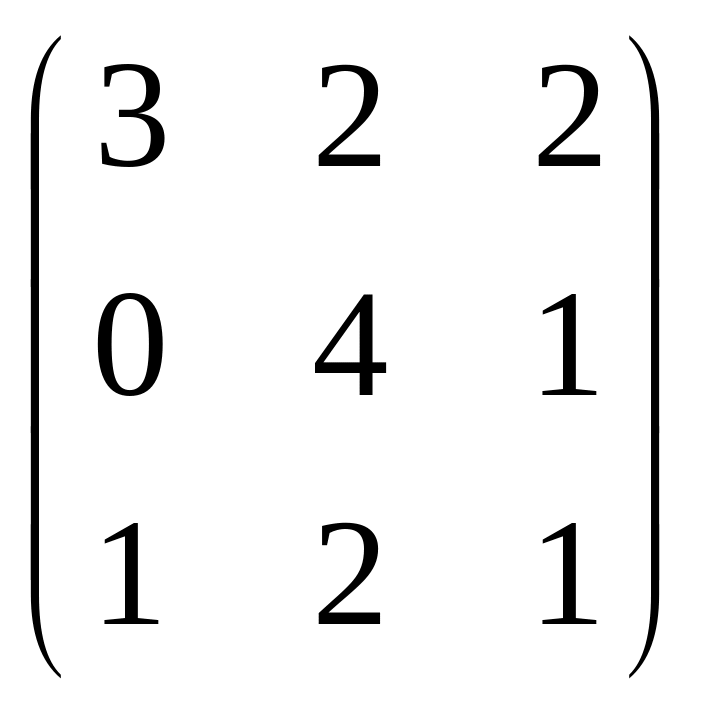
14.
![]() 3
A =
3
A =
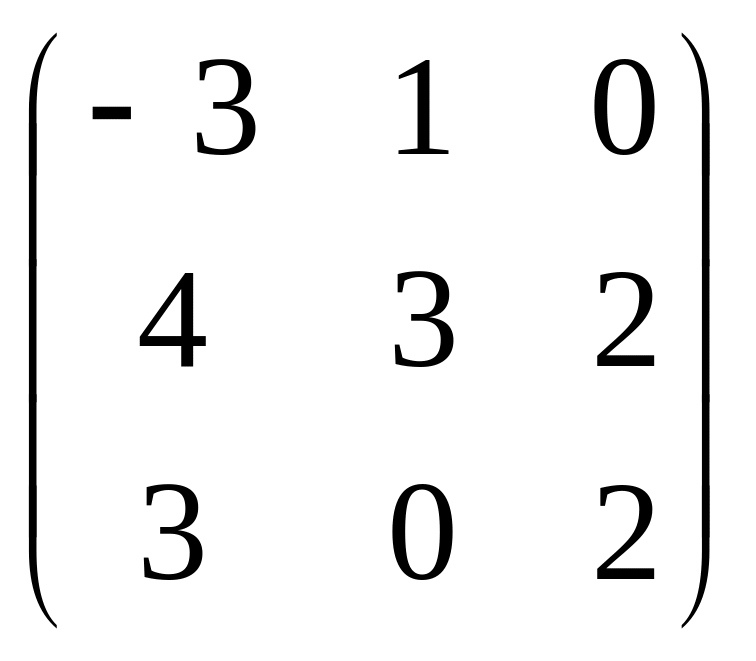
15.
A=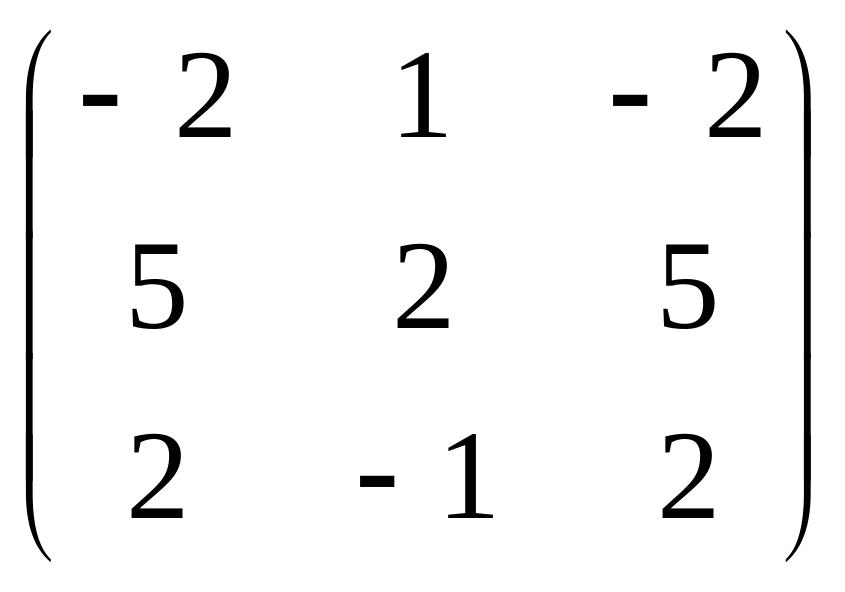
16.
![]() A=
A=
17.
![]() A =
A =
18.
![]() A =
A =
19.
![]() A =
A =
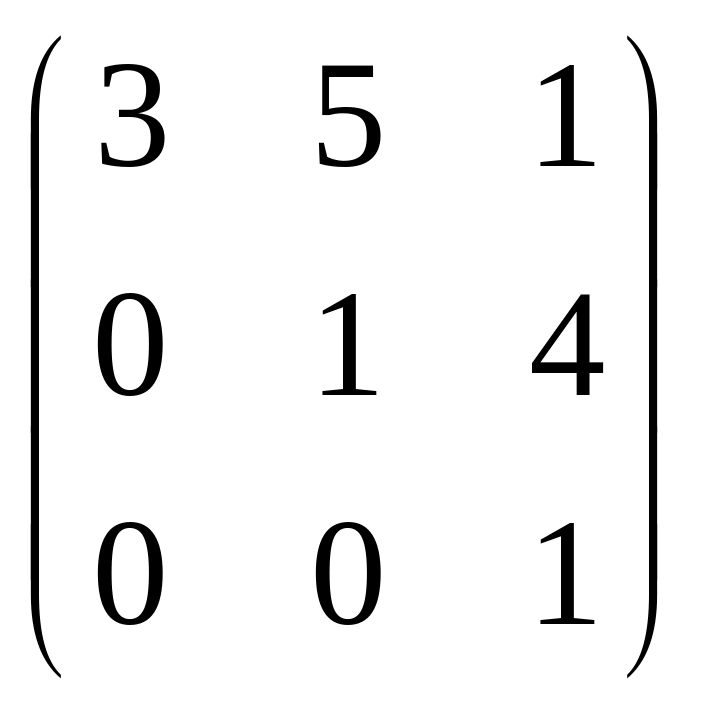
20.
A =

21. A=
22.
A =
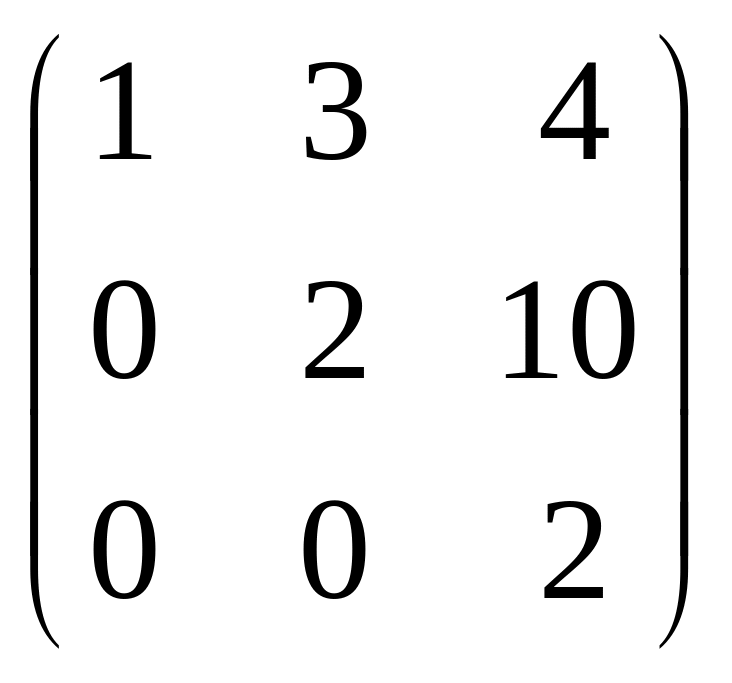
23.
![]() A =
A =
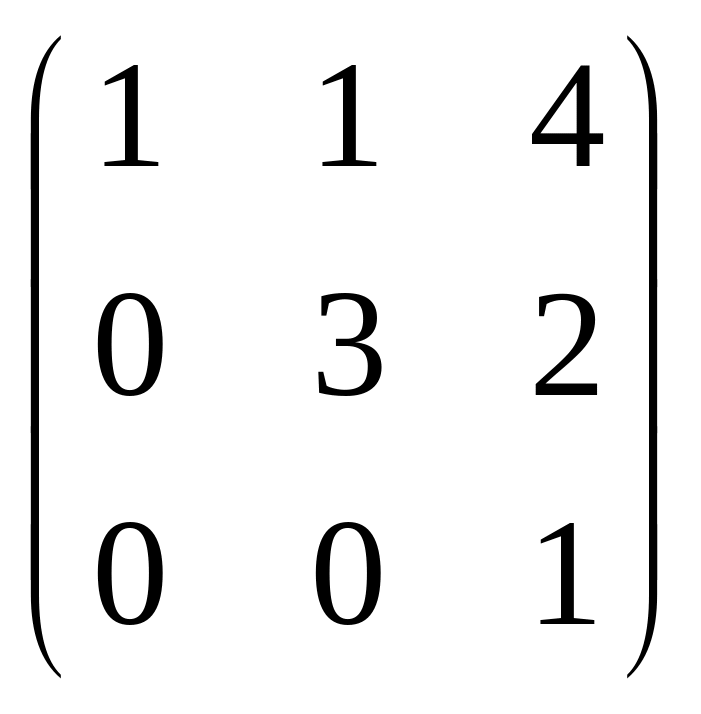
24.
A =
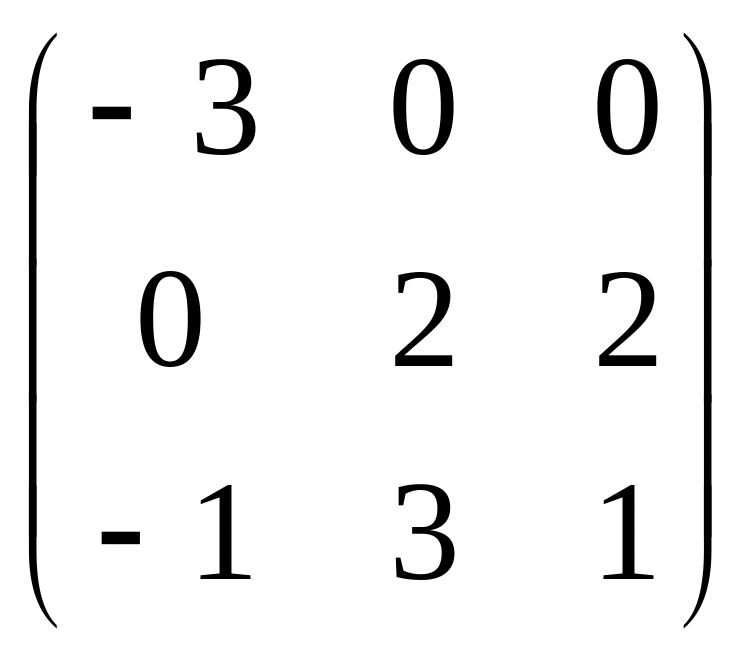
25.
![]() A =
A =
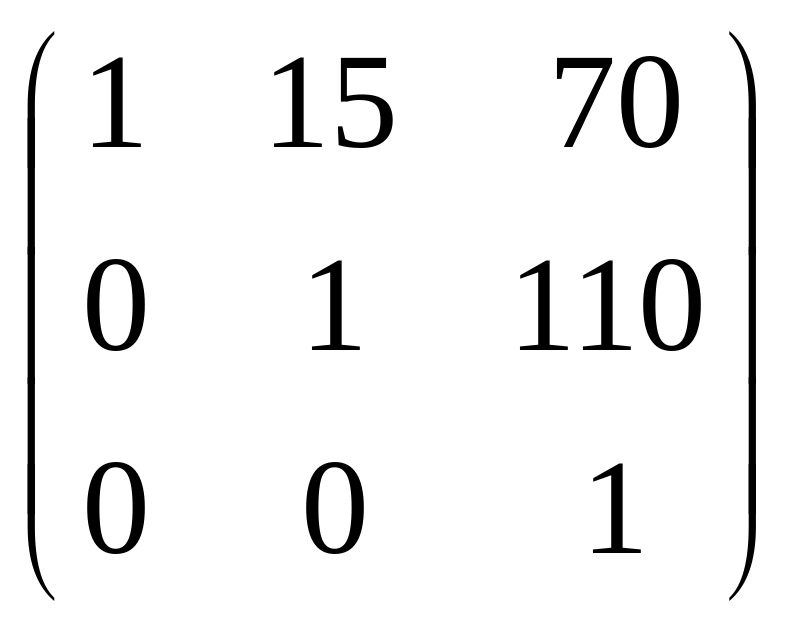
26.
![]() A =
A =

27.
A =

28.
A =
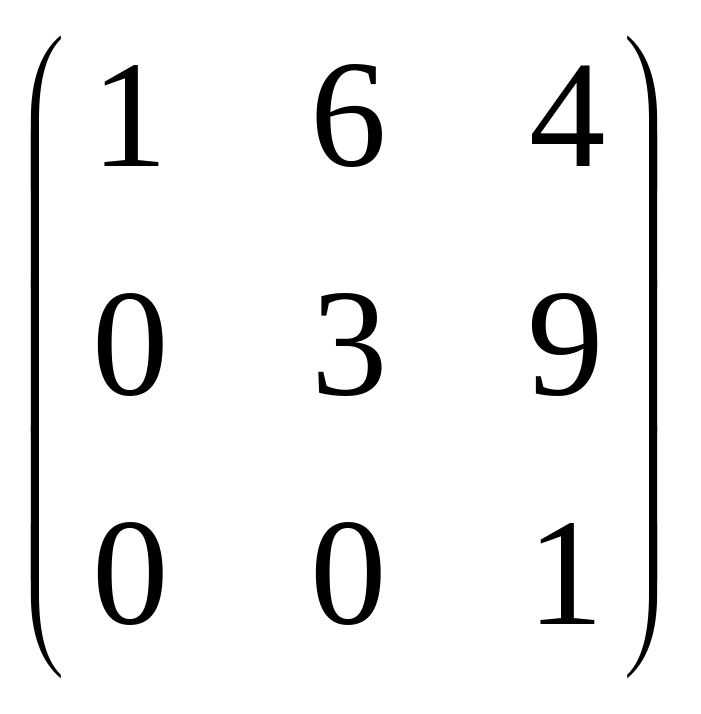
29.
A =
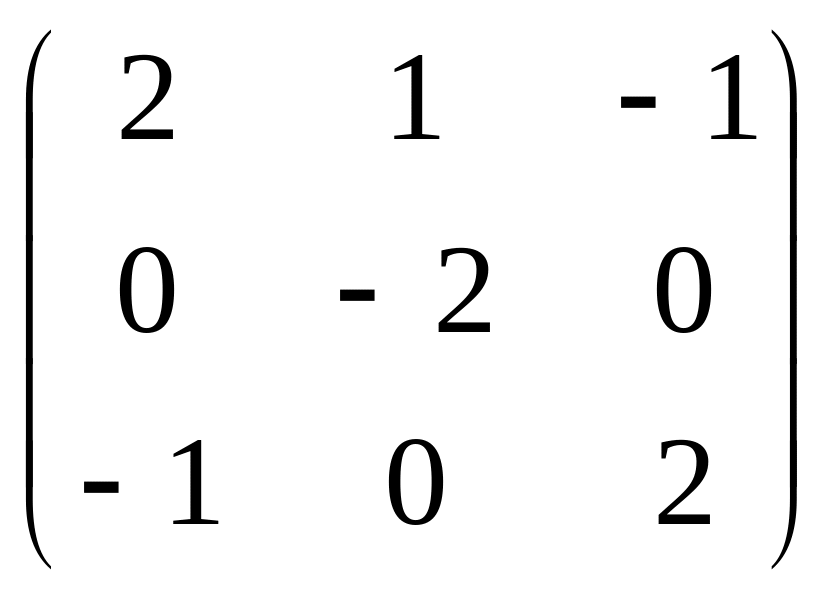
30.
A =
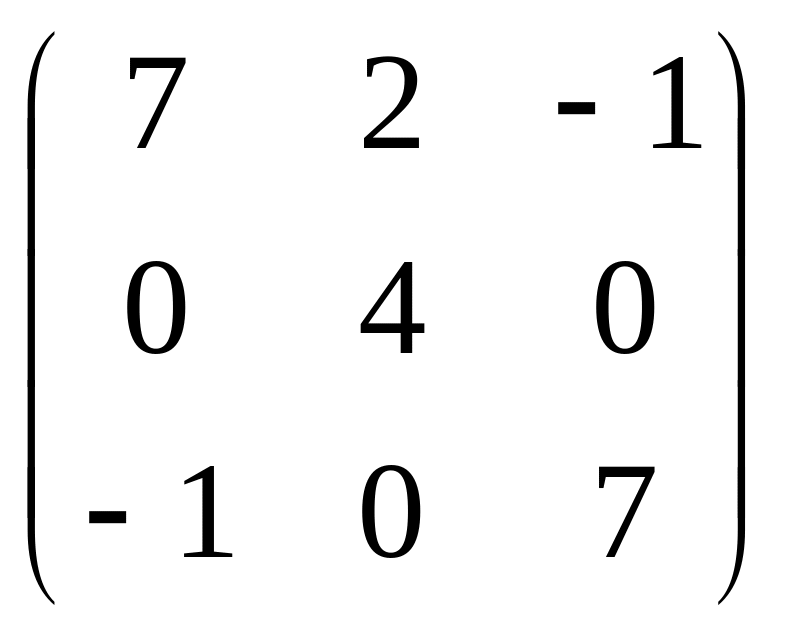
5.Матричные уравнения
5.1. Вопросы по теории
Матричные уравнения и их применение
Перестановочные матрицы
Переходные матрицы
Решение уравнения AX=B
Решение уравнения AX=XB и AX=XA
Решение уравнения AX-XB=C
5.2. Примеры решения задач
1. Решим матричное уравнение A X = B
![]() X=
X=![]() ,
,
где A — квадратная невырожденная ( det A ≠ 0 ) матрица порядка n , B — матрица размера n × m и X — неизвестная матрица.
Так как матрица A — невырожденная, то существует обратная матрица A-1 . Умножим обе части уравнения слева (операция умножения матриц некоммутацивна) на матрицу A-1 . Получим
(A-1A)X=A-1B
EX=A-1B
X=A-1B
Таким образом, искомое решение матричного уравнения определяется формулой
X=A-1B
Обратите внимание на то, что количество строк матрицы B должно быть равно порядку матрицы A .
X=![]() =
=![]() .
.
2. Рассмотрим уравнение вида AX=XB
![]() X=X
X=X![]() (1)
(1)
Найдем жорданову форму матриц A и B.
![]() =
=![]()
![]() =
=![]()
Найдем соответствующие матрицы перехода U и V методом Гаусса из уравнения AU=U и BV=V .
U =
 V=
V=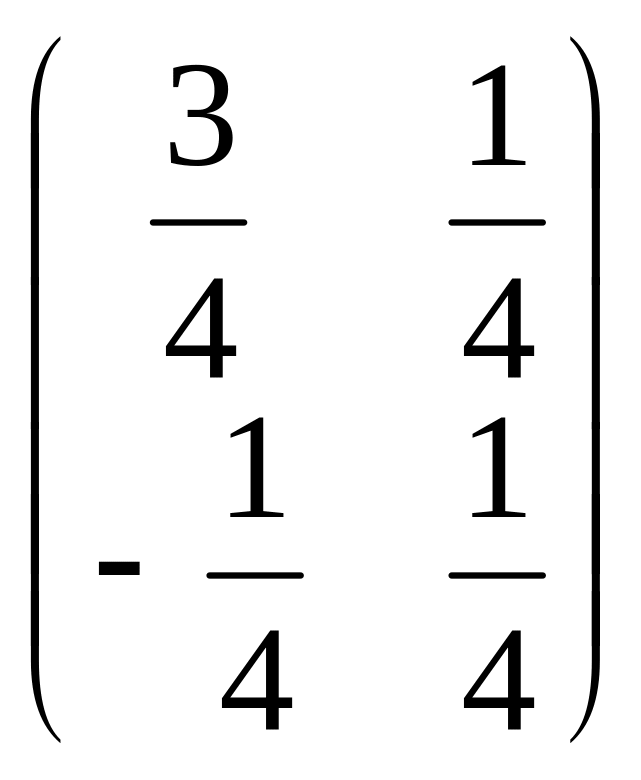
A=U U-1 B=V V-1 Подставим данные равенства в уравнение (1)
U U-1X=X V V-1
Умножим слева на U-1 и справа на V
U-1XV=U-1XV
Обозначим через
![]() =
U-1XV
и сведем исходное уравнение к более
простому
=
U-1XV
и сведем исходное уравнение к более
простому
= . Методом Гаусса найдем .
=
X= U V-1
6.Нормы матриц
6.1 Вопросы по теории:
Евклидова норма
Октаидрическая норма
Кубическая норма
Эквивалентность норм в конечномерном пространстве, теорема Люстерника
Спектральный радиус
Свойсива норм
Сингулярные числа
6.2 Примеры решения задач
Пусть дана матрица A=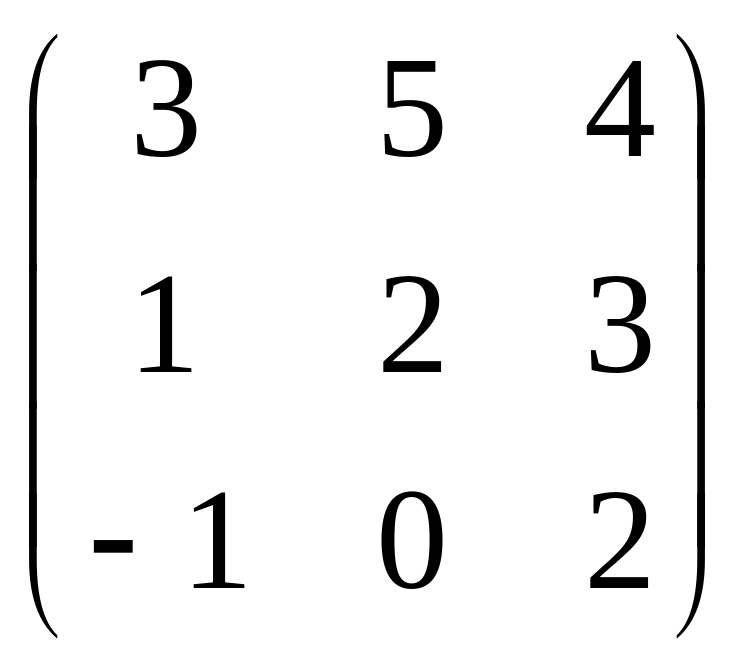 .
Вычислим ее евклидову, октаидрическую
и кубическую нормы:
.
Вычислим ее евклидову, октаидрическую
и кубическую нормы:
![]() Е=
Е=![]() =
=![]()
![]() =
=![]() =21
=21
К=![]()
![]()
![]() =15
=15
2. Рассмотрим матрицу с комплексными
элементами B=![]() .
.
![]() =
=![]()
![]() E
=
E
=
![]()
O
= 4+![]() +
+![]()
K = 9
Если требуется сохранить смысловые связи данных матрицы, то можно вычислять также такие нормы, как
1=![]()
![]() ,
,
![]() =
=![]() и др.
и др.
