Министерство Образования

Республики Беларусь

Учреждение образования “Гомельский Государственный

Университет имени Франциска Скорины”

Кривденко О.В., Куриленко Ю.В., Губенко Е.К.

Под редакцией Васильева А.Ф.

Матричный анализ

Практическое пособие для студентов

математических специальностей.

Гомель, 2009

Содержание

Предисловие…………………………………………………………………………

1. Блочные матрицы и операции над ними……………………………………………..4

2. МП-матрицы…………………………………………………………………………...5

3. Жорданова нормальная форма матрицы, ее существование и единственность…..6

4. Функция от матриц………………………………………………………………….....7

5. Матричные уравнения…………………………………………………………………8

6. !Разложение матриц……………………………...…………………………………….9

7. Норма матриц…………………………………………………………………………10

8. !Матричные модели к экономике……………...…………………………………….12

Ответы

Литература

Предисловие

1. Блочные матрицы и операции над ними

1.1. Вопросы теории

1. Разбиение матрицы на блоки

2. Сложение блочных матриц

3. Умножение блочной матрицы на число

4. Умножение блочных матриц

5. Формула Фробениуса (обратная матрица)

1.2. Примеры решения задач

Пусть даны матрицы M=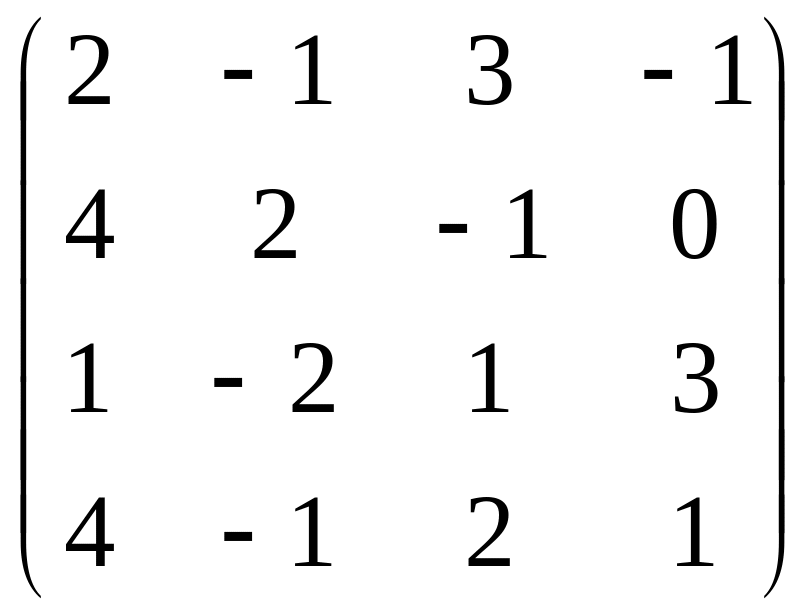 и N= .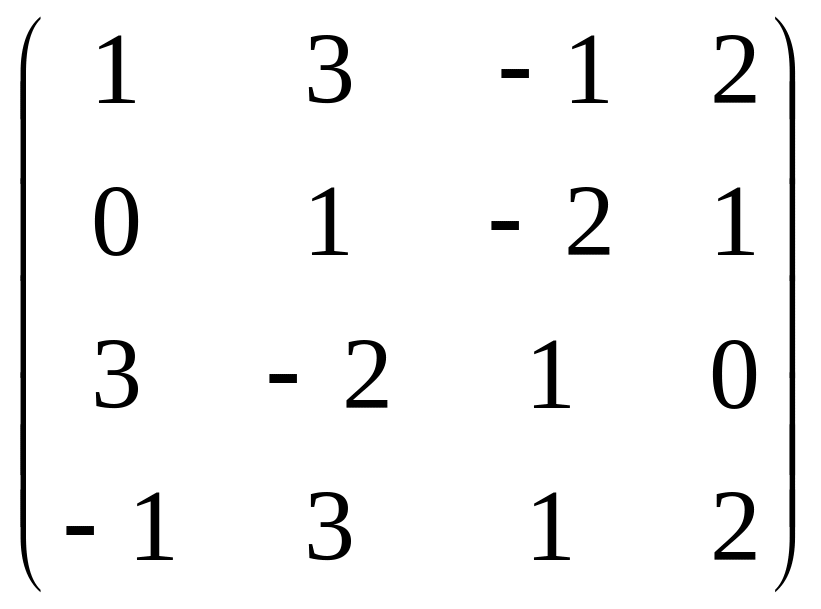

Разобьем ее на блоки:

А= , B= , C= , D= ;

E= , L= , F= , P= .

Тогда матрицы M и N можно записать в следующем виде:

M= , N= .

При умножении блочной матрицы на число умножается каждый блок на это число по обычному правилу умножения матрицы на число.

M = , если =2, то M=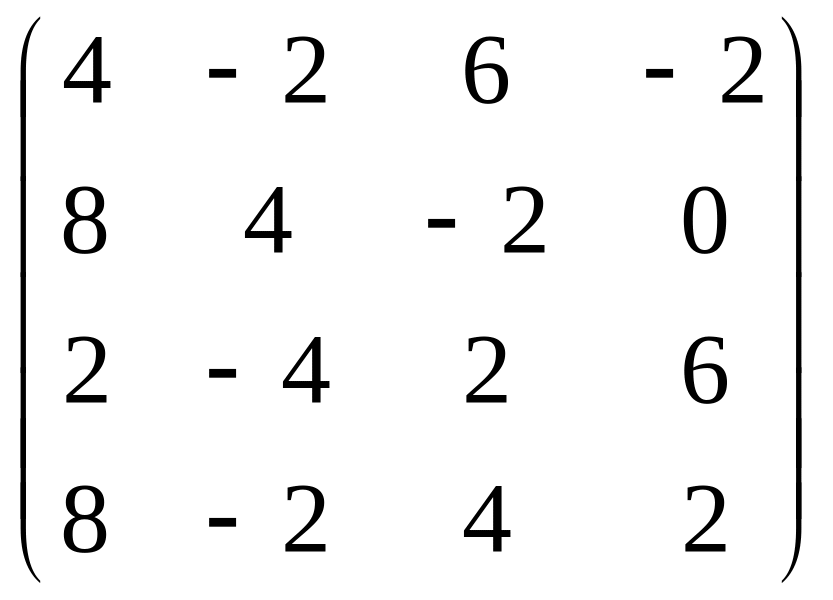

При сложении блочных матриц матрицы должны быть одинаковых размеров и одинаково разбиты на блоки. Руководствуясь формальными правилами сложения, как в случае, когда вместо блоков стоят числовые элементы, получим, что

X=M+N= = .

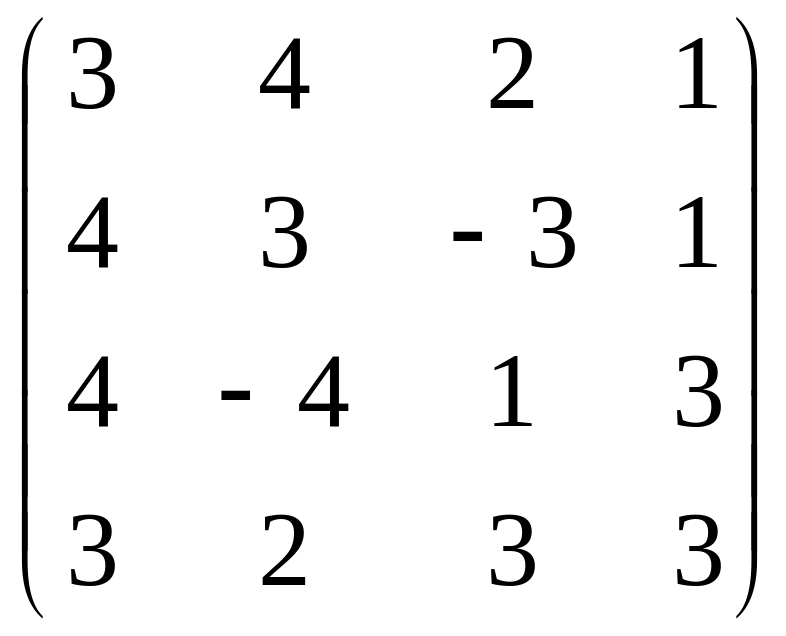При умножении блочных матриц M и N дополнительно требуется, чтобы длина строк матрицы М совпадала с высотой столбцов матрицы N, а при разбиении все горизонтальные размеры в первом сомножителе совпадали с соответствующими вертикальными размерами второго сомножителя.

X=NM= (X )= , где t- количество блоков в строке первого

сомножителя и в столбце второго.

X =AE+BF X₁₂=AL+BP X₂₁=CE+DF X₂₂=CL+DP

X₁₁= X₁₂= X₂₁= X₂₂=

Таким образом, матрица X примет вид:

X= .

При изучении блочных матриц особый интерес представляет нахождение обратной матрицы. Для этого существует формула Фробениуса. Найдем с помощью этой формулы обратную матрицу к матрице М.

A^-1+ A^-1BH^-1CA^-1 =

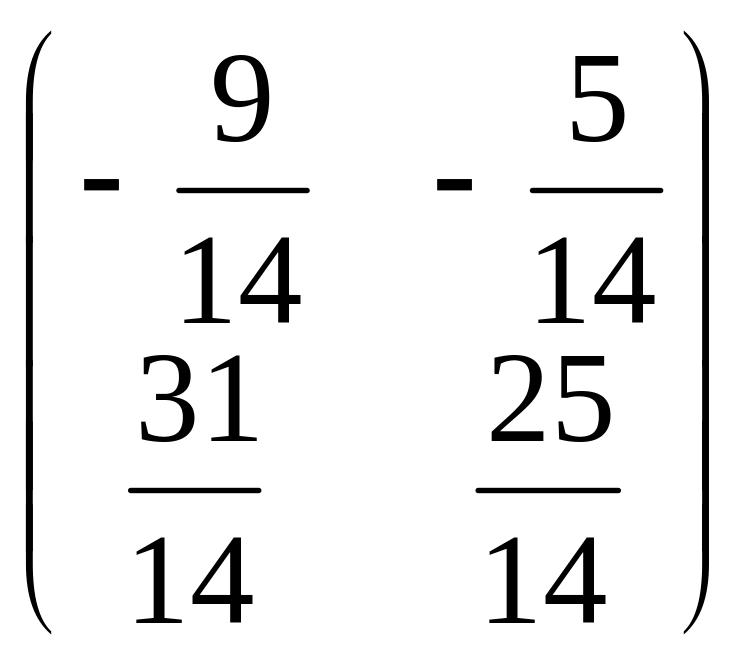
- A^-1BH^-1 =

- H^-1CA^-1 =

H^-1=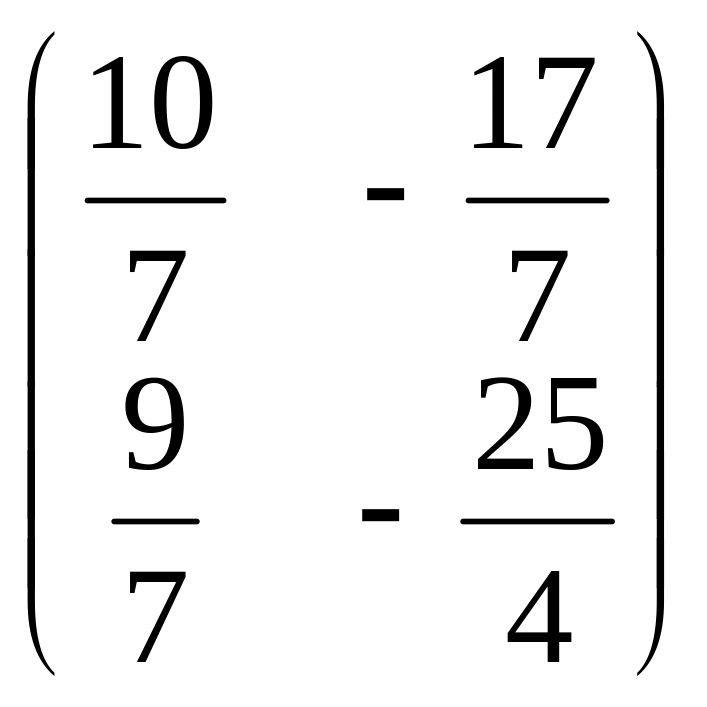

1.3. Примеры для самоконтроля

2.МП-матрицы

2.1. Вопросы теории

1. Понятие псевдообратной матрицы

2. Скелетное разложение

3. Существование и единственность псевдообратной матрицы

4. Свойства псевдообратной матрицы

5. Нормальное псевдорешение системы линейных уравнений

2.2. Примеры решения задач

Пусть дана система линейных уравнений.

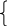x₁ - x₂ + 2x₃ + 3x₄ =1;

-x₁ + 2x₂ + x₃ + 2x₄ =2;

-2x₁ + 4x₂ + 2x₃ + 4x₄ =1.

Найдем нормальное псевдорешение и длину невязки.

Решим систему.

Запишем расширенную матрицу и найдем ее ранг.

= ~

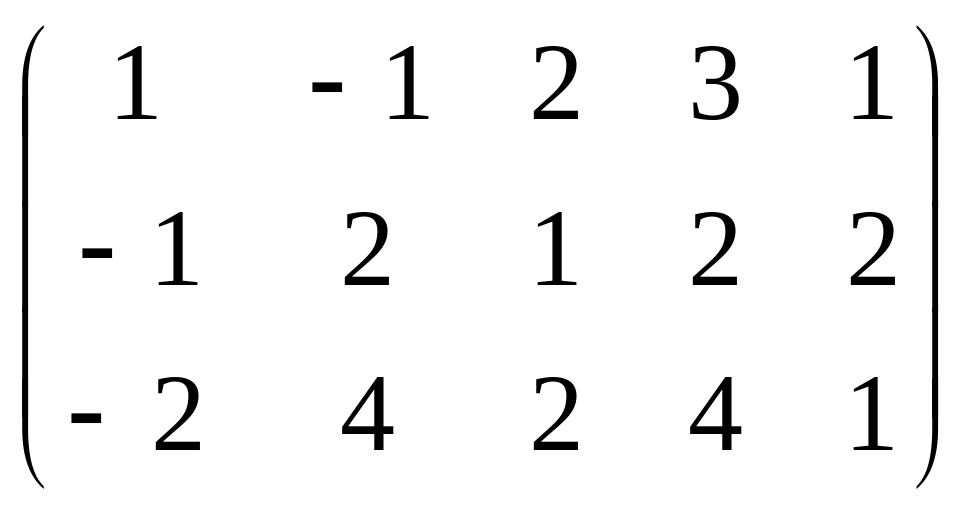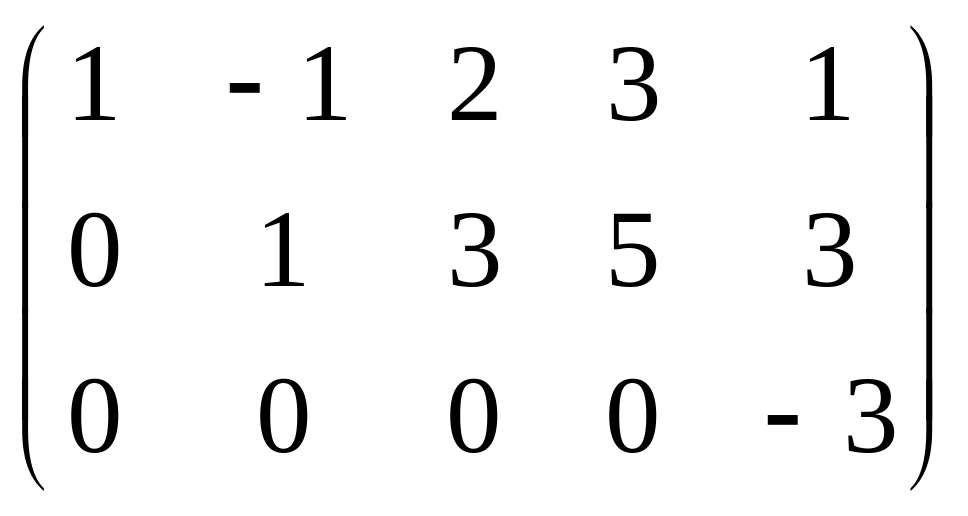
rang M=2 rang =3, значит система несовместна.

Псевдорешение (столбец, длина невязки которого минимальна) X₀=M⁺N, где N = – столбец, элементы которого свободные члены системы.

Найдем псевдообратную матрицу M⁺.

Приведем к ступенчатому виду матрицу M.

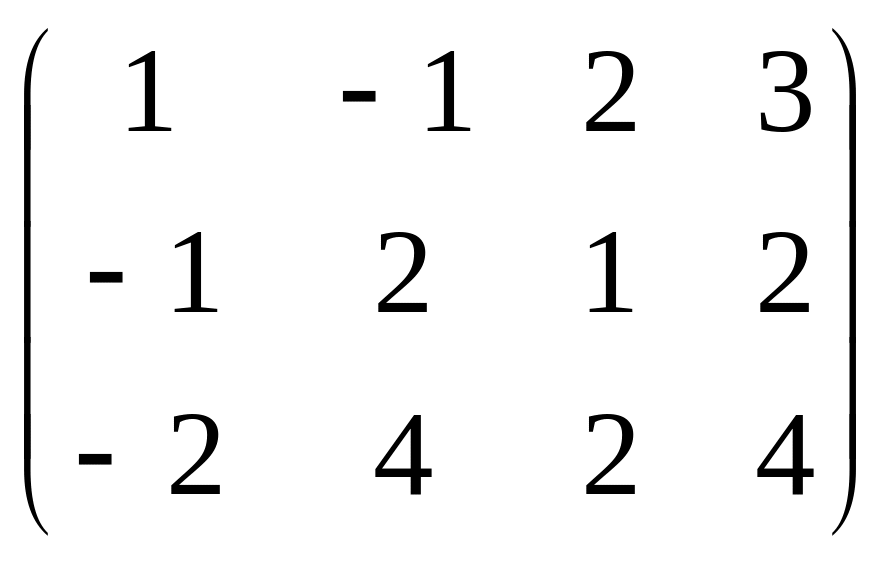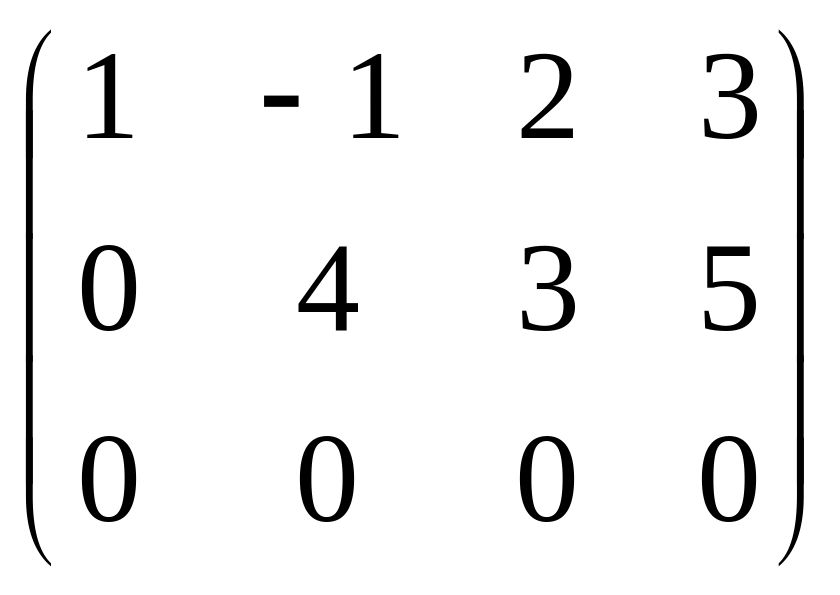~ . Тогда r = rang M=2.

Найдем скелетное разложение матрицы М.

Выберем r = 2 произвольных линейно независимых столбцов матрицы M и объявим их столбцами матрицы B.

B=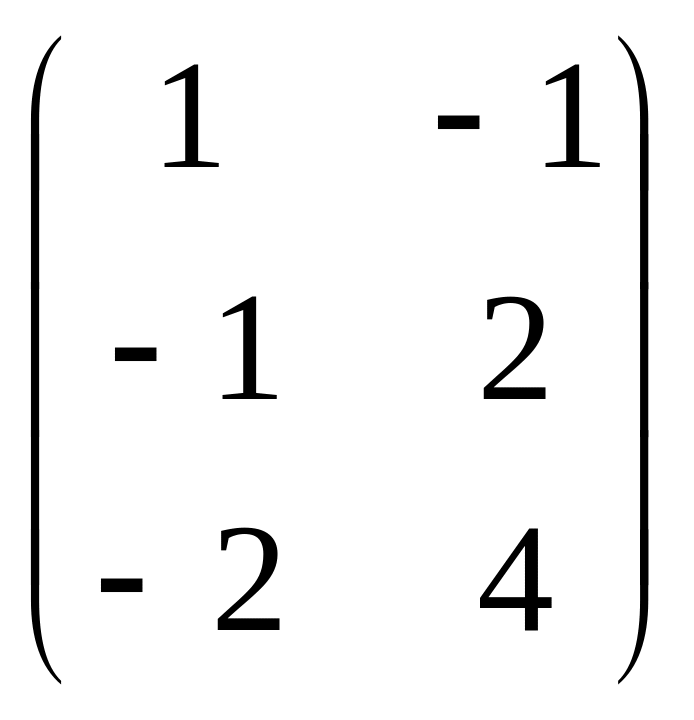

Таким образом матрица M=BC, где С – матрица коэффициентов.

~ ~ ~

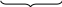
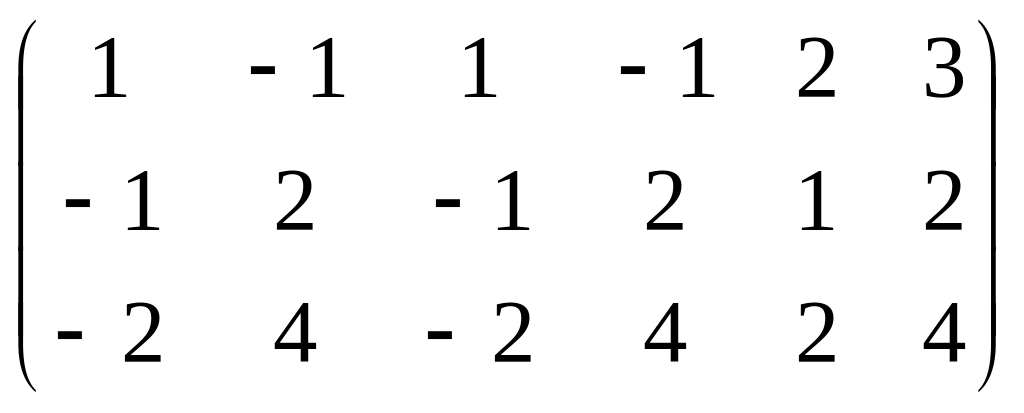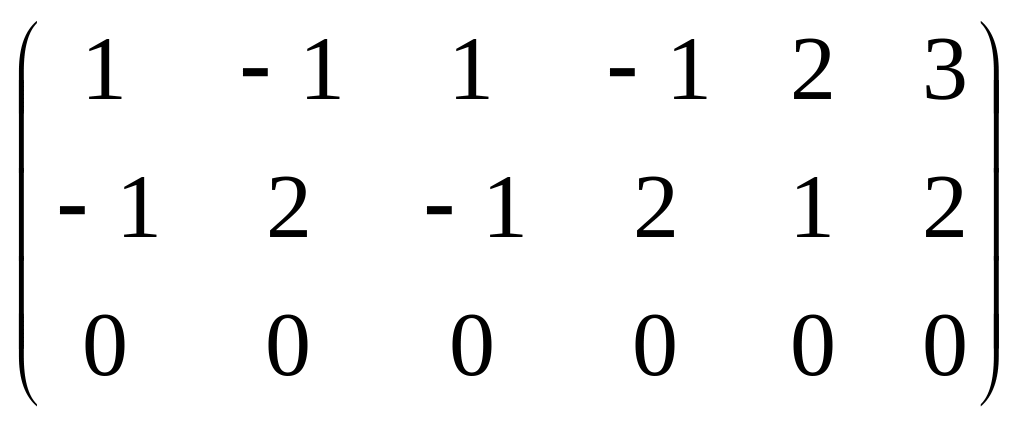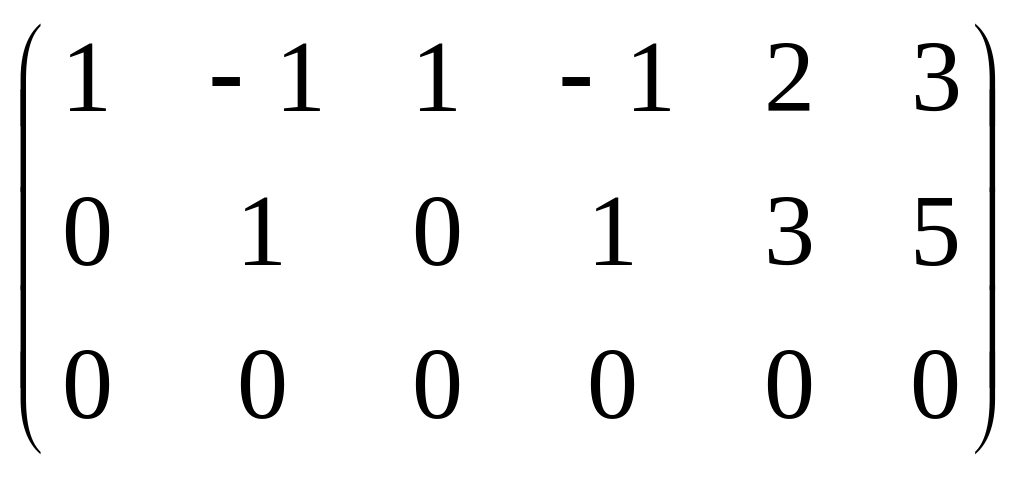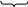
^{матрица B дополнение}

~ .

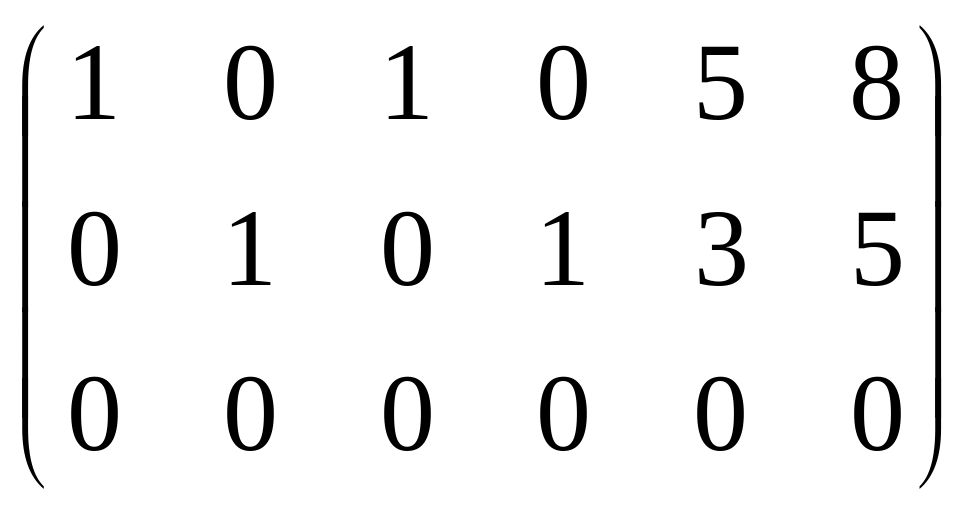Отсюда C=

C^*=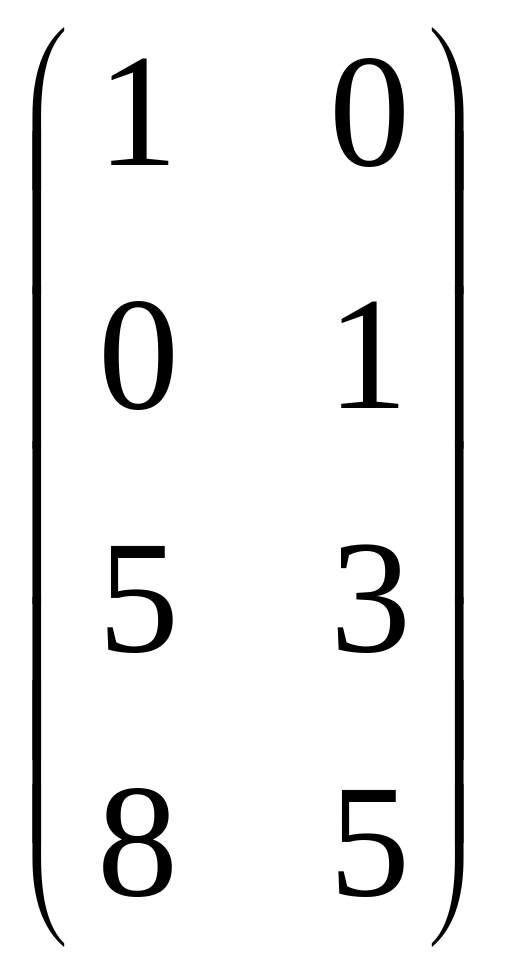

B^*= , где оператор ^* - сопряжение и транспонирование.

CC^*= =

(CC^*)^-1=

B^*B= =

(B^*B)^-1=

Построим матрицу M⁺= C^*(CC^*)^-1(B^*B)^-1 B^*= .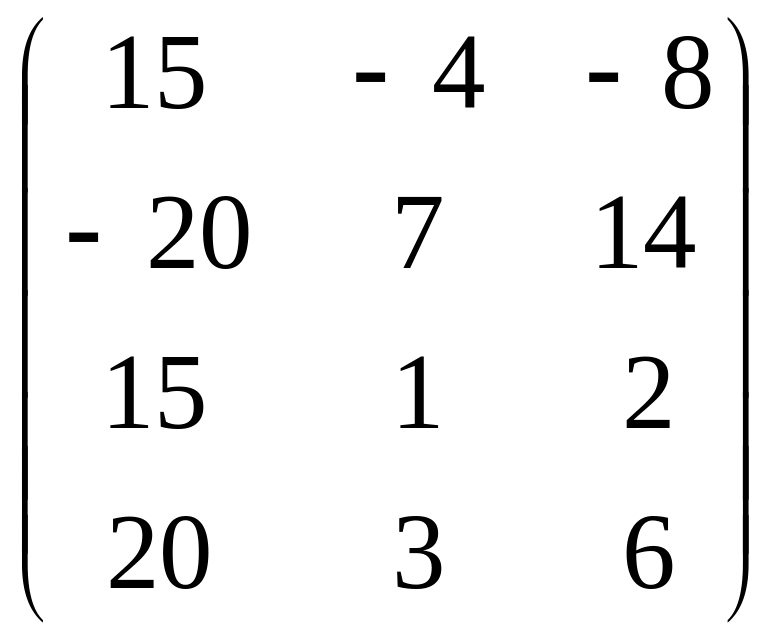

X₀=M⁺N = = - псевдорешение.

Найдем невязку системы N-MX₀.

MX₀ = = =

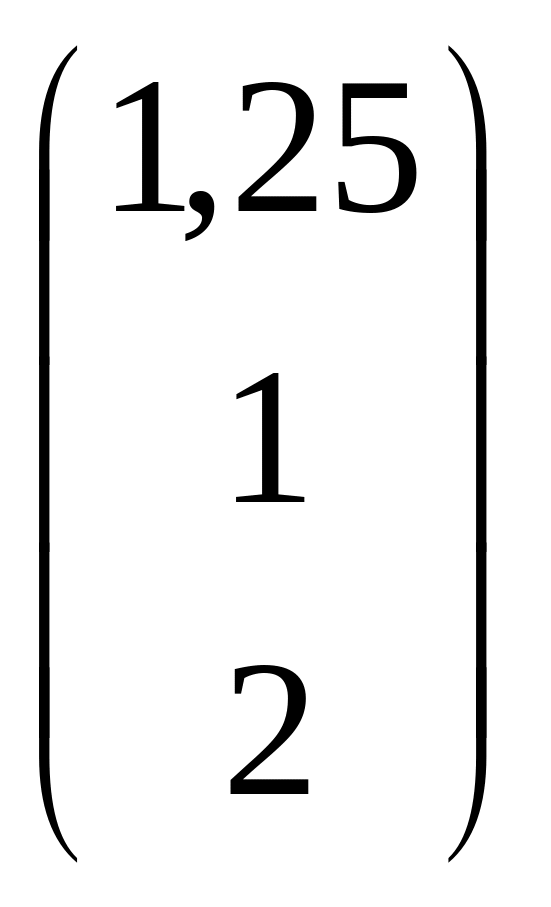
N-MX₀ = - = .

Найдем длину невязки (корень из суммы квадратов координат). |N-MX₀| = =