1. Сущность проецирования. Виды проецирования. Общие свойства проецирования.

Метод проецирования заключается в том, что любая точка

пространства может быть спроецирована с помощью проецирующих

лучей на любую поверхность. Ортогональное проецирование - это

такой метод, когда проецирующие лучи параллельны между собой и

перпендикулярны к плоскости проекций.

ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

В методе центрального проецирования все проецирующие лучи

проходят через общую точку S.

ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

Если центр проекций S – бесконечно удаленная точка, то все

проецирующие лучи параллельны между собой. Для проведения этих

лучей задается направление проецирования

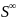
. Общие свойства проецирования.

1. Проекцией точки является точка.

2. Проекцией прямой линии – прямая (частный случай: проекция

прямой – точка, если прямая проходит через центр проекций).

3. Если точка в пространстве инцидентна (принадлежит) линии,

то проекция этой точки принадлежит проекции данной линии.

Для параллельного проецирования характерны еще два свойства:

 Проекции параллельных прямых, также

параллельны.

 Отношение длин параллельных отрезков равны

отношению длин их проекций: =

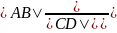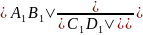
| 2. Ортогональная модель. Метод Монжа. Изображение точки на эпюре Монжа.

Сущность метода ортогонального проецирования заключается в том, что предмет проецируется на две взаимно перпендикулярные плоскости лучами, ортогональными (перпендикулярными) к этим двум плоскостям

. Линия пересечения плоскостей проекций называется осью проекций (координат) и обозначается ОХ.

При построении проекций необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость.

Чтобы получить плоский чертеж, плоскость 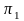совмещают вращением вокруг оси ОХ с плоскостью .

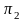Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещены определенным образом одна с другой, называется эпюром Монжа (рис.9).

Проекции одной и той же точки на две взаимно перпендикулярные плоскости располагаются на прямой, перпендикулярной оси проекций х₁₂.Эта прямая называется направлением проецирования или линией проекционной связи.

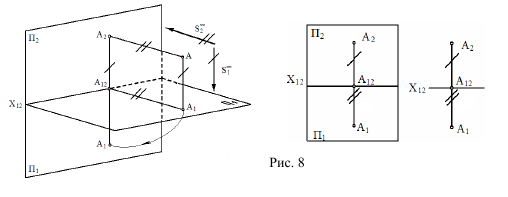
3. Изображение линии на эпюре Монжа. Определитель линии. Прямая общего положения. Принадлежность точки линии.

Моделью прямой линии на эпюре Монжа в общем случае является пара прямых. Геометрическим определителем прямой линии служат две точки.

плоскостей проекции, способ вращения вокруг проецирующей прямой, вращение вокруг плоскости уровня.

Способ перемены плоскостей проекции. Алгоритм построения:

Вводиться дополнительная плоскость проекции П4, рас-положенную перпендикулярно П1 и произвольно П2. Происходит замена одной из основных плоскостей проекции. В данном случае происходит замена фронтальной плоскости П2.

В новой системе плоскостей проекции П1/П4 из точки А1опускается перпендикуляр к оси х1,4.

Расстояние от точки А2 до оси х1,2 откладывается на полученном перпендикуляре в дополнительной плоскости П4 от оси х1,4

Способ вращения

Алгоритм построения:

Задаётся ось вращения, перпендикулярная одной из плоскостей проекции. В данном случае ось i перпендикулярна горизонтальной плоскости П1.

Точка А1 двигаясь вокруг центра вращения i1 ≡ O1 проецируется на плоскость П1 без искажения и преобразуется в новую горизонтальную проекцию А1

По линиям связи находится фронтальная проекция точки А1’

Способ вращения вокруг линии уровня

Алгоритм построения:

Задаётся ось вращения, относительно одной из основных плоскостей проекций. В данном случае за ось вращения взята горизонталь h.

Для определения радиуса вращения в плоскости П1 строиться прямоугольный треугольник

О1А1А1’.При этом за катет прямоугольного треугольника принимается горизонтальная проекция О1А1.Второй катет находится превышением высот точки А2

. 3. Пересечением дуги окружности, проведённой из горизонтальной проекции центра вращения О1 с радиусом R с горизонтальным следом плоскости ƩП1 находится точка А1’’.

По линиям связи находится фронтальная проекция точки А2’’