34. Поиск глобального минимума одномерной функции: сравнение алгоритмов метода ломаных и метода покрытий.

Метод Ломанных:

Метод применим к функциям, удовлетворяющим условию Липшица.

Функция f(x)заданная на отрезке [a, b] удовлетворяет условию Липшица, если существует такая постояннаяL>0, что

где L –постоянная Липшица.

Процесс построения ломаной функции начинается с выбора произвольной начальной точки и вычисления функции – точка С0. Из точки С0 построим два отрезка - С0 – A0 иC0 –B0 с угловыми наклонамиLи-Lсоответственно.

Ломаная линия A0 -B0 -C0 - первое приближение целевой функции.

Следующая точка x1 выбирается из условия наименьшего значения ординаты точкиm0. Совершенно очевидно, минимальное значение ордината точки примет лишь при условии, когда абсцисса точки совпадает с правой границей интервала [a, b].

Метод покрытий:

35. Поиск минимума многомерной функции: метод покоординатного спуска.

Нахождение минимума многомерной функции:

Целевая функция – функция, описывающая (n+1)-мерную поверхность.

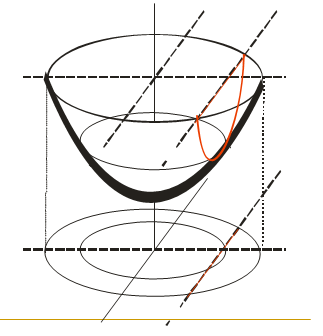
Алгоритм покоординатного спуска:

Шаг 1: Фиксируем значение y1.ФункцияF(x,y)зависит только отx - F(x,y1)

Шаг 2: находим минимум F(x,y1) в точке x1.

Шаг 3:Фиксируем значение x1.ФункцияF(x,y)зависит только отy - F(x1,y)

Шаг 4: находим минимум F(x1,y) в точке y2.

Шаг 5: Фиксируем значение y2.ФункцияF(x,y)зависит только отx - F(x,y2)

Шаг 6: находим минимум F(x,y2) в точке x2.

Шаг 7:Фиксируем значение x2.ФункцияF(x,y)зависит только отx - F(x2,y)

Шаг 8: находим минимум F(x2,y) в точке y3.

Условия выхода:

Значения функции F(x,y) на двух соседних итерациях меньше малого числаε

Интервал между локальными минимумами на двух соседних итерациях меньше малого числа δ

36. Поиск минимума многомерной функции: симплекс-метод.