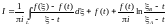- •Множества, области, кривые.
- •Комплексная плоскость.
- •Односвязные и многосвязные области.
- •Последовательности комплексных чисел.
- •Предел последовательности комплексных чисел.
- •6.Понятие функции комплексной переменной.
- •7.Предел и непрерывность функции комплексной переменной.
- •8.Основные элементарные функции комплексной переменной.
- •9.Определение производной. Дифференцирование функции комплексной переменной.
- •10.Дифференциал. Условия Коши-Римана.
- •Аналитическая функция.
- •Гармонические функции. Сопряженно-гармонические функции.
- •13.Геометрический смысл модуля производной. Коэффициент подобия.
- •14. Геометрический смысл аргумента производной.
- •Понятие о конформном отображении.
- •Конформное отображение 1-го рода. Конформное отображение 2-го рода.
- •Критерий конформности.
- •Принцип взаимно-однозначного соответствия границ.
- •Принцип симметрии Римана-Шварца. Примеры функций, задающих конформное отображение
- •Определение интеграла от функции комплексной переменной.
- •21.Связь интеграла комплексной переменной с криволинейным интегралом 2-го рода.
- •22.Свойства интеграла от фкп.
- •Оценка интеграла от функции комплексной переменной.
- •Основная теорема Коши. Теорема Коши для многосвязной области.
- •Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница.
- •Интеграл Коши.
- •27.Теорема о среднем для аналитических функций.
- •Принцип максимума модуля аналитической функции.
- •Интеграл типа Коши
- •Теорема Коши-Лиувилля.
- •Теорема Морера.
- •Числовые ряды с комплексными членами. Частичная сумма ряда.
- •Необходимое и достаточное условия сходимости числового ряда.
- •Функциональные ряды. Точка сходимости. Область сходимости.
- •Равномерная сходимость функциональных рядов.
- •Степенные ряды. Круг и радиус сходимости степенного ряда.
- •Ряд Тейлора. Разложение в ряд Тейлора некоторых элементарных функций комплексной переменной.
- •Формулы Эйлера.
- •Голоморфные функции.
- •Нули аналитической функции.
- •Ряд Лорана. Область сходимости ряда Лорана.
- •Разложение аналитической функции в ряд Лорана.
- •Классификация изолированных особых точек аналитической функции.
- •Устранимая особая точка.
- •Полюс. Порядок полюса.
- •Существенно особая точка.
- •Теорема Сохотского.
- •Разложение аналитической функции в ряд Лорана в окрестности бесконечно удаленной точки.
- •Понятие вычета. Основная теорема о вычетах.
- •Вычисление вычетов для простого полюса.
- •Вычисление вычетов для полюса порядка n.
- •Логарифмический вычет
- •Вычет относительно бесконечно удаленной точки.
- •Теорема о сумме вычетов.
- •Вычисление интегралов по замкнутому контуру.
- •Вычисление с помощью вычетов определенных интегралов от рациональных функций действительной переменной
- •Вычисление с помощью вычетов определенных интегралов от тригонометрических функций.
- •58.Вычисление с помощью вычетов несобственных интегралов от функций
- •Лемма Жордана.
- •Суммирование некоторых рядов с помощью вычетов Формула суммирования знакопеременного ряда с рациональными слагаемыми.
Интеграл Коши.
Рассмотрим
некоторую функцию f(z),
голоморфную в односвязной области D.
На контуре L
функция не обязательно голоморфна, но
обязательно непрерывна. Она также
непрерывно продолжима на контур L
из любой внутренней точки области D.
Пусть
 - некоторая внутренняя точка области
- некоторая внутренняя точка области
 .
.

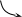

При
этом справедлива формула
 - формула
Коши.
- формула
Коши.
Доказательство:
Рассмотрим
функцию
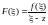 - голоморфную в области D
за исключением точки
- голоморфную в области D
за исключением точки
 с координатой
,
где она не определена.
с координатой
,
где она не определена.
Окружим точку М(z) контуром Г. Тогда по теореме Коши для многосвязных областей получим

Т ак
как функция
ак
как функция
 голоморфна повсюду, кроме точки z,
то контур Г – произвольный. Нужно лишь,
чтобы он охватывал точку M
и лежал внутри контура
голоморфна повсюду, кроме точки z,
то контур Г – произвольный. Нужно лишь,
чтобы он охватывал точку M
и лежал внутри контура
 .
В качестве Г возьмём окружность, радиус
которой стремится к нулю.
.
В качестве Г возьмём окружность, радиус
которой стремится к нулю.
Введём локальную систему координат с центром в точке M. Пусть
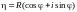 .
Выполним предельный переход
.
Выполним предельный переход

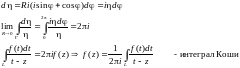
27.Теорема о среднем для аналитических функций.
1. Значения
аналитической в некоторой области
функции полностью определяются её
значениями на границе этой области.
Этот факт можно сформулировать в виде
теоремы о среднем. Возьмём
 такое, что окружность
такое, что окружность
 радиуса
с центром в
лежит в D1.
Тогда
радиуса
с центром в
лежит в D1.
Тогда
 ,
и
,
и
 .
Поэтому справедлива
.
Поэтому справедлива
2. Теорема о среднем. Значение аналитической функции в каждой точке z0 равно среднему арифметическому её значений на любой окружности с центром в точке z0.
Теорема доказана
в предположении, что точка z0
лежит внутри контура L.
Если z0
находится вне контура, то
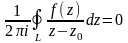 ,
так как подынтегральная функция
аналитична в
,
так как подынтегральная функция
аналитична в
 .
.
3 .
Формула справедлива и для многосвязной
области, если под кривой L
подразумевать полную границу области.
В дальнейшем нам понадобится такой
вариант:
аналитична в замкнутом кольце, ограниченном
окружностями
.
Формула справедлива и для многосвязной
области, если под кривой L
подразумевать полную границу области.
В дальнейшем нам понадобится такой
вариант:
аналитична в замкнутом кольце, ограниченном
окружностями
 и
.
Тогда для всех z,
лежащих внутри кольца,
и
.
Тогда для всех z,
лежащих внутри кольца,
 ;
при этом окружности проходятся так, что
область остаётся слева. В последней
формуле переобозначены переменные:
;
при этом окружности проходятся так, что
область остаётся слева. В последней
формуле переобозначены переменные:
 .
.
Принцип максимума модуля аналитической функции.
Теорема (принцип максимума модуля): пусть ф-ия f(z) голом-на в D и непрерывна вD. Тогда max|f(z)| достигается на D границе обл. D.
Док-во: D – компакт, f(z) непр. наD, max|f(z)| достигается.
1) f(z)const, D max|f(z)| достигается.
2) f(z) не const, по th (о постоянстве ф-ии, достигающей локального max во внутр. точке) max|f(z)| не может достигаться во внутр. обл. D, достигается на D.
Интеграл типа Коши
Интеграл типа Коши является обобщением интеграла Коши.
Н а
дуге АВ
задана функция f(t),
не обязательно аналитическая,
удовлетворяющая дуге АВ
условию Гельдера:
а
дуге АВ
задана функция f(t),
не обязательно аналитическая,
удовлетворяющая дуге АВ
условию Гельдера:
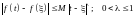
где - некоторое положительное число. Построим аналитическую функцию
 -
интеграл
типа Коши.
-
интеграл
типа Коши.
F(z)
является
аналитической во всей плоскости за
исключением контура L.
В бесконечно удалённой точке

Найдём
предельное значение функции F(z)
при
 ,
где t
– точка контура, не совпадающая с точками
А
и В.
,
где t
– точка контура, не совпадающая с точками
А
и В.
Пусть слева от контура.


Первое слагаемое – сингулярный интеграл.


Получим

Аналогично находим

Объединяя полученные равенства, получим

 -
формулы
Сохоцкого-Племеля.
-
формулы
Сохоцкого-Племеля.
Рассмотрим
частный случай: контур
замкнут, а функция
 является граничным значением функции
является граничным значением функции
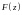 ,
то есть
,
то есть
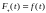 .
В этом случае интеграл типа Коши переходит
в интеграл Коши. Кроме того, теперь если
точка
лежит вне контура
,
то, в соответствии с теоремой Коши
.
В этом случае интеграл типа Коши переходит
в интеграл Коши. Кроме того, теперь если
точка
лежит вне контура
,
то, в соответствии с теоремой Коши
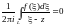
Следовательно,
 .
Из формул Сохоцкого-Племеля следует
.
Из формул Сохоцкого-Племеля следует

Полученное соотношение, справедливое для граничных значений аналитической функции, называется тождеством Племеля.
Рассмотрим задачу вычисления сингулярного интеграла

Рассмотрим первый интеграл:

Таким образом, первый интеграл не является несобственным.

-
точка
 обходится слева. Окончательно получим
обходится слева. Окончательно получим