
- •Множества, области, кривые.
- •Комплексная плоскость.
- •Односвязные и многосвязные области.
- •Последовательности комплексных чисел.
- •Предел последовательности комплексных чисел.
- •6.Понятие функции комплексной переменной.
- •7.Предел и непрерывность функции комплексной переменной.
- •8.Основные элементарные функции комплексной переменной.
- •9.Определение производной. Дифференцирование функции комплексной переменной.
- •10.Дифференциал. Условия Коши-Римана.
- •Аналитическая функция.
- •Гармонические функции. Сопряженно-гармонические функции.
- •13.Геометрический смысл модуля производной. Коэффициент подобия.
- •14. Геометрический смысл аргумента производной.
- •Понятие о конформном отображении.
- •Конформное отображение 1-го рода. Конформное отображение 2-го рода.
- •Критерий конформности.
- •Принцип взаимно-однозначного соответствия границ.
- •Принцип симметрии Римана-Шварца. Примеры функций, задающих конформное отображение
- •Определение интеграла от функции комплексной переменной.
- •21.Связь интеграла комплексной переменной с криволинейным интегралом 2-го рода.
- •22.Свойства интеграла от фкп.
- •Оценка интеграла от функции комплексной переменной.
- •Основная теорема Коши. Теорема Коши для многосвязной области.
- •Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница.
- •Интеграл Коши.
- •27.Теорема о среднем для аналитических функций.
- •Принцип максимума модуля аналитической функции.
- •Интеграл типа Коши
- •Теорема Коши-Лиувилля.
- •Теорема Морера.
- •Числовые ряды с комплексными членами. Частичная сумма ряда.
- •Необходимое и достаточное условия сходимости числового ряда.
- •Функциональные ряды. Точка сходимости. Область сходимости.
- •Равномерная сходимость функциональных рядов.
- •Степенные ряды. Круг и радиус сходимости степенного ряда.
- •Ряд Тейлора. Разложение в ряд Тейлора некоторых элементарных функций комплексной переменной.
- •Формулы Эйлера.
- •Голоморфные функции.
- •Нули аналитической функции.
- •Ряд Лорана. Область сходимости ряда Лорана.
- •Разложение аналитической функции в ряд Лорана.
- •Классификация изолированных особых точек аналитической функции.
- •Устранимая особая точка.
- •Полюс. Порядок полюса.
- •Существенно особая точка.
- •Теорема Сохотского.
- •Разложение аналитической функции в ряд Лорана в окрестности бесконечно удаленной точки.
- •Понятие вычета. Основная теорема о вычетах.
- •Вычисление вычетов для простого полюса.
- •Вычисление вычетов для полюса порядка n.
- •Логарифмический вычет
- •Вычет относительно бесконечно удаленной точки.
- •Теорема о сумме вычетов.
- •Вычисление интегралов по замкнутому контуру.
- •Вычисление с помощью вычетов определенных интегралов от рациональных функций действительной переменной
- •Вычисление с помощью вычетов определенных интегралов от тригонометрических функций.
- •58.Вычисление с помощью вычетов несобственных интегралов от функций
- •Лемма Жордана.
- •Суммирование некоторых рядов с помощью вычетов Формула суммирования знакопеременного ряда с рациональными слагаемыми.
Оценка интеграла от функции комплексной переменной.
- произвольные комплексные постоянные);
2. - кривые без общих внутренних точек):
3. - кривая, совпадающая с L, но проходимая в противоположном направлении;
4. Если l - длина кривой L, , то .
Основная теорема Коши. Теорема Коши для многосвязной области.
Теорема Коши для
односвязной области.
Если D
- односвязная ограниченная область,
- аналитическая в этой области функция,
то для любого кусочно-гладкого замкнутого
контура L,
лежащего в D,
интеграл от
по L
равен нулю:
 .
.
Доказательство.
Удивительно, но эта важнейшая теорема
непосредственно и просто следует из
условий Коши-Римана и формулы Грина.
Так как, по доказанному выше,

 ,
то, применяя к действительным криволинейным
интегралам формулу Грина, получим
,
то, применяя к действительным криволинейным
интегралам формулу Грина, получим
 ,
так как, по из условиям Коши-Римана
,
так как, по из условиям Коши-Римана
 .
Символом G
в доказательстве обозначена область,
заключённая внутри контура L.
.
Символом G
в доказательстве обозначена область,
заключённая внутри контура L.
Т еорема
Коши для многосвязной области.
Если функция
аналитична в замкнутой многосвязной
ограниченной области
еорема
Коши для многосвязной области.
Если функция
аналитична в замкнутой многосвязной
ограниченной области
 ,
ограниченной контурами
,
ограниченной контурами
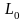 (внешняя граница),
,
,
…,
(внешняя граница),
,
,
…,
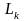 ,
то интеграл от
,
взятый по полной границе области
,
проходимой так, что область остаётся с
одной стороны, равен нулю.
,
то интеграл от
,
взятый по полной границе области
,
проходимой так, что область остаётся с
одной стороны, равен нулю.
Доказательство
и здесь воспроизводит доказательство
формулы Грина для многосвязной области.
Рассмотрим случай, когда граница области
(на рисунке область заштрихована) состоит
из внешнего контура
и внутренних контуров L1
и L2.
Соединим контур
разрезом
FM
с контуром L1,
разрезом BG
- с контуром L2
Область
 с границей
с границей
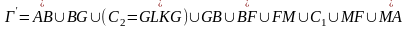 односвязна, поэтому для неё справедлива
интегральная теорема Коши:
односвязна, поэтому для неё справедлива
интегральная теорема Коши:
![]() .
Интегралы по каждому из разрезов входят
в этот общий интеграл дважды в
противоположных направлениях и, как
следствие, взаимно уничтожаются, поэтому
остаются только интегралы по контурам,
проходимым так, что область остаётся с
одной стороны.
.
Интегралы по каждому из разрезов входят
в этот общий интеграл дважды в
противоположных направлениях и, как
следствие, взаимно уничтожаются, поэтому
остаются только интегралы по контурам,
проходимым так, что область остаётся с
одной стороны.
В
дальнейшем нам понадобится другая
формулировка этой теоремы. Буквами без
верхнего индекса будем обозначать
контуры, проходимые против часовой
стрелки, с верхним минусом - по часовой.
Мы доказали, что
 .
Таким образом, интеграл
по внешнему контуру равен сумме интегралов
по внутренним контурам,
при этом все контуры обходятся в одном
направлении.
.
Таким образом, интеграл
по внешнему контуру равен сумме интегралов
по внутренним контурам,
при этом все контуры обходятся в одном
направлении.
Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница.
Первообразная
аналитической функции. Если
функция
аналитична в односвязной области D,
то, как мы доказали, интеграл по кривой
 зависит только от начальной и конечной
точек и не зависти от формы кривой. Если
зафиксировать начальную точку
,
то интеграл будет зависеть только от
конечной точки z,
поэтому можно написать
зависит только от начальной и конечной
точек и не зависти от формы кривой. Если
зафиксировать начальную точку
,
то интеграл будет зависеть только от
конечной точки z,
поэтому можно написать
 .
Можно доказать (также, как мы доказывали
существование потенциальной функции
в односвязной области при выполнении
условия
.
Можно доказать (также, как мы доказывали
существование потенциальной функции
в односвязной области при выполнении
условия
 ),
что справедлива следующая
),
что справедлива следующая
Теорема.
Для любой аналитической в области D
функции
интеграл
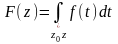 является аналитической в D
функцией, и
является аналитической в D
функцией, и

Любая функция
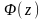 такая, что
такая, что
 ,
называется первообразной функции
.
Любые две первообразные отличаются не
более, чем на постоянную, поэтому
,
называется первообразной функции
.
Любые две первообразные отличаются не
более, чем на постоянную, поэтому
 ,
откуда при
,
откуда при
 получаем
получаем
 ,
или
,
или
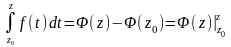 .
Таким образом, для аналитических функций
справедлива формула Ньютона-Лейбница,
и основные приёмы интегрирования:
.
Таким образом, для аналитических функций
справедлива формула Ньютона-Лейбница,
и основные приёмы интегрирования:
 .
.
