14. Геометрический смысл аргумента производной.
Р
авенство
означает, что
,
где
.
Отсюда, в частности, следует, что если
функция дифференцируема в точке, то она
непрерывна в этой точке. Будем писать
,
пренебрегая слагаемым высшего порядка
малости. Пусть в точке z
существует
.
Возьмём точки
и
;
пусть
,
тогда
.
таким образом,
в
больше
,
больше
на
для
любого
(с точностью до бесконечно малых высшего
порядка). Следовательно, в окрестности
любой точки z,
в которой
,
отображение
действует следующим образом: любой
вектор
растягивается в
раз и поворачивается на угол
.
Понятие о конформном отображении.
П
усть
через точку z
проходят две гладкие кривые
и
,
касательные
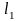и
к которым образуют с осью Ох
углы, соответственно,
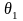и
.
Образы этих кривых
и
при дифференцируемом отображении
имеют касательные
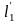и
,
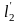образующие с действительной осью Ou
углы
и
.
Согласно предыдущему пункту,
,
,
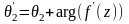т.е.
.
Таким образом, дифференцируемое
отображение при
сохраняет углы между кривыми. Сохраняется
и направление отсчёта углов (т.е. если
>
,
то
>
).
Любое преобразование плоскости в плоскость, обладающее эти свойством (т.е. свойством сохранения углов), называется конформным.
Св-ва конф. отобр-ий:
1) постоянство растяжений. Линейное растяжение всех кривых, проход. ч\з т. z0 при конф. отобр.-ии. Коэф. лин. растяж. K=|f(z0)|.
2) постоянство угла поворота. При конф. отобр. все кривые проход. ч\з т.z0 поворачиваются на 1 и тот же угол равный аргументу f(z0).
3) отобр., обратное к конф.-му явл-ся конф.-ым.
4) суперпозиция конф. отобр-ий есть конф. отобр-ие.
Конформное отображение 1-го рода. Конформное отображение 2-го рода.
П
усть
через точку z
проходят две гладкие кривые
и
,
касательные
и
к которым образуют с осью Ох
углы, соответственно,
и
.
Образы этих кривых
и
при дифференцируемом отображении
имеют касательные
и
,
образующие с действительной осью Ou
углы
и
.
Согласно предыдущему пункту,
,
,
т.е.
.
Таким образом, дифференцируемое
отображение при
сохраняет углы между кривыми. Сохраняется
и направление отсчёта углов (т.е. если
>
,
то
>
).
Если при этом сохраняется направление отсчёта углов, то преобразование называется конформным преобразованием первого рода; если направление отсчёта углов меняется на противоположное, то преобразование называется конформным преобразованием второго рода. Мы доказали, что аналитическая в некоторой области G функция осуществляет конформное отображение первого рода во всех точках, в которых производная отлична от нуля.
Пример конформного
отображения второго рода - недифференцируемая
функция
.
Критерий конформности.
Теорема.
Пусть
и
– две произвольные односвязные области,
границы
которых состоят более чем из одной
точки. Тогда существует
и только одно конформное отображение
области
на
область
такое,
что
,
, (1)
где
,
,
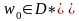– заданное действительное число
(рис.3.2).
Условия (1) называются условиями нормировки конформного отображения. Вместо (1) можно задать другие условия. Например, можно задать
,
,
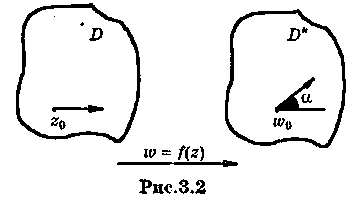где
,
– внутренние, а
,
– граничные
точки областей
и
соответственно,
или
,
,
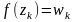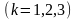где
,
,
–
различные граничные точки области
,
а
,
,
– различные
граничные точки области
,
причем точки
,
,
и
,
,
следуют
в порядке положительного обхода границ
и
областей
и
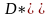соответственно.
Теорема Римана устанавливает факт существования функции, конформно отображающей область на область , но не даёт удобного способа построения её. Кроме того, эта функция выражается через элементарные функции лишь для простых областей. Поэтому изучение частных случаев отображений с помощью комбинаций элементарных функций имеет большое практическое значение.