
- •Множества, области, кривые.
- •Комплексная плоскость.
- •Односвязные и многосвязные области.
- •Последовательности комплексных чисел.
- •Предел последовательности комплексных чисел.
- •6.Понятие функции комплексной переменной.
- •7.Предел и непрерывность функции комплексной переменной.
- •8.Основные элементарные функции комплексной переменной.
- •9.Определение производной. Дифференцирование функции комплексной переменной.
- •10.Дифференциал. Условия Коши-Римана.
- •Аналитическая функция.
- •Гармонические функции. Сопряженно-гармонические функции.
- •13.Геометрический смысл модуля производной. Коэффициент подобия.
- •14. Геометрический смысл аргумента производной.
- •Понятие о конформном отображении.
- •Конформное отображение 1-го рода. Конформное отображение 2-го рода.
- •Критерий конформности.
- •Принцип взаимно-однозначного соответствия границ.
- •Принцип симметрии Римана-Шварца. Примеры функций, задающих конформное отображение
- •Определение интеграла от функции комплексной переменной.
- •21.Связь интеграла комплексной переменной с криволинейным интегралом 2-го рода.
- •22.Свойства интеграла от фкп.
- •Оценка интеграла от функции комплексной переменной.
- •Основная теорема Коши. Теорема Коши для многосвязной области.
- •Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница.
- •Интеграл Коши.
- •27.Теорема о среднем для аналитических функций.
- •Принцип максимума модуля аналитической функции.
- •Интеграл типа Коши
- •Теорема Коши-Лиувилля.
- •Теорема Морера.
- •Числовые ряды с комплексными членами. Частичная сумма ряда.
- •Необходимое и достаточное условия сходимости числового ряда.
- •Функциональные ряды. Точка сходимости. Область сходимости.
- •Равномерная сходимость функциональных рядов.
- •Степенные ряды. Круг и радиус сходимости степенного ряда.
- •Ряд Тейлора. Разложение в ряд Тейлора некоторых элементарных функций комплексной переменной.
- •Формулы Эйлера.
- •Голоморфные функции.
- •Нули аналитической функции.
- •Ряд Лорана. Область сходимости ряда Лорана.
- •Разложение аналитической функции в ряд Лорана.
- •Классификация изолированных особых точек аналитической функции.
- •Устранимая особая точка.
- •Полюс. Порядок полюса.
- •Существенно особая точка.
- •Теорема Сохотского.
- •Разложение аналитической функции в ряд Лорана в окрестности бесконечно удаленной точки.
- •Понятие вычета. Основная теорема о вычетах.
- •Вычисление вычетов для простого полюса.
- •Вычисление вычетов для полюса порядка n.
- •Логарифмический вычет
- •Вычет относительно бесконечно удаленной точки.
- •Теорема о сумме вычетов.
- •Вычисление интегралов по замкнутому контуру.
- •Вычисление с помощью вычетов определенных интегралов от рациональных функций действительной переменной
- •Вычисление с помощью вычетов определенных интегралов от тригонометрических функций.
- •58.Вычисление с помощью вычетов несобственных интегралов от функций
- •Лемма Жордана.
- •Суммирование некоторых рядов с помощью вычетов Формула суммирования знакопеременного ряда с рациональными слагаемыми.
Вычисление интегралов по замкнутому контуру.
Теорема Руше.
ЕСЛИ G
– односвязная область, С – замкнутый
контур, ограничивающий G,
и
аналитические в G
и на С,
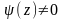 на
С,
на
С,
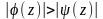 на
С,
на
С,
 -
сумма кратностей всех лежащих в G
нулей функции
,
-
сумма кратностей всех лежащих в G
нулей функции
,
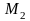 -
сумма кратностей всех лежащих в G
нулей функции
+
,
ТО
-
сумма кратностей всех лежащих в G
нулей функции
+
,
ТО
 .
.
Док-во:
1)
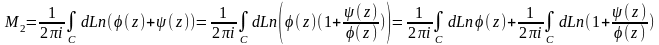
2 )
)

3)


w
Вектор
из начала координат в точку, при такой
конфигурации образа С, ни одного оборота
не совершит.
 .
.
4)
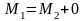
Вычисление с помощью вычетов определенных интегралов от рациональных функций действительной переменной
Интеграл
типа

R(x)- рациональная ф-ия от х
 CR=[-R,
R]R
CR=[-R,
R]R
R={zC: |z|=R, Imz>0}

Лемма (о вычислении интеграла по действительной прямой через вычеты):
пусть f(z) голоморфна в верхней полупл-ти за искл. конечного числа особых точек a1,…,an и непрерывна вплоть до границы. Если выполняется: 1) -+f(х)dх сх-ся; 2) lim(при R) Rf(z)dz=0, тогда выполняется следующее

где суммирование
ведётся по особым точкам ф-ции f(z), лежащим в верхней полупл-ти Im ak>0.
Док-во: рассмотрим контур CR=[-R,R]R. R={zC: |z|=R Im z>0};
Выберем R достаточно большим так, чтобы все особые точки ф-ции f(z) (a1,…,an) попали вовнутрь CR (можно, т.к. n-конечно). Вычисляем интеграл по этому контуру:

Теперь R, получим -RRf(z)dz-+f(x)dx.
Rf(z)dz0 в силу условия леммы,

Замечание.
Если вычислять интеграл через вычеты
в особых точках, лежащих в нижней
полуплоскости, то в правой части ф-лы
возникает знак «-»:

Вычисление с помощью вычетов определенных интегралов от тригонометрических функций.
Интеграл типа
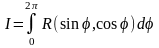
R(u,v) – ф-ия 2-х переменных.
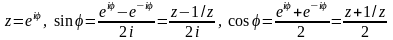

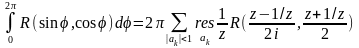
где суммирование ведется по особым точкам, попавшим внутрь единичного круга.
58.Вычисление с помощью вычетов несобственных интегралов от функций
действительной переменной.
Теорема.
Если
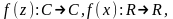
 при x=z,
при x=z,
 -изолированная
особая точка f(z),
имеет в
нуль не ниже II
порядка,
не имеет особых точек на действительной
оси,
имеет конечное число особых точек, то
-изолированная
особая точка f(z),
имеет в
нуль не ниже II
порядка,
не имеет особых точек на действительной
оси,
имеет конечное число особых точек, то
 ,
где
,
где
 распространяется
на особые точки, лежащие выше действительной
оси.
распространяется
на особые точки, лежащие выше действительной
оси.
Док-во:
Возьмем круг такого радиуса, чтобы на нем и вне его не было особых точек, кроме бесконечности.
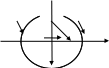
Y
R
-R R x


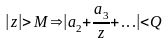
 .
.
Лемма Жордана.
Лемма (Жордана): пусть >0 и выполняются условия: 1) g(z) непрерывна в {zC: |z|R0>0, Im z0}; 2) M(R)=max(по zR)|g(z)|0 при R {zC: |z|=R, Imz>0}. Тогда limRR eizg(z)dz=0.
Док-во: z=Rei, [0,], dz=Rieid.
|


 eiz|=|exp(i(Rcos+iRsin))|=|exp(-Rsin+iRcos)|
exp(-Rsin)exp(-R2/).
eiz|=|exp(i(Rcos+iRsin))|=|exp(-Rsin+iRcos)|
exp(-Rsin)exp(-R2/).
y
y=2/ [0,/2], sin2/.

