49. Вычисление вычетов для полюса порядка n.

Если а - полюс функции n-го порядка, то .

Док-во. Так как точка - полюс n-го порядка функции , то. 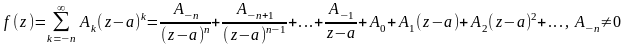. Для того, чтобы удалить особенность в точке а, умножим на 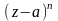: 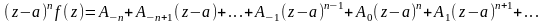. Теперь, чтобы убрать первые члены этой формулы и добраться до 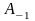, дифференцируем это произведение n-1 раз: ,

,

……………………………………………………………………………………………………………………….,

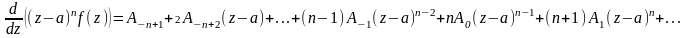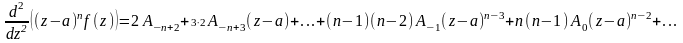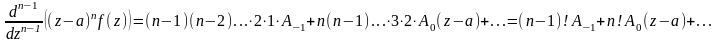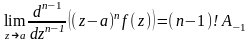, , откуда и следует доказываемая формула.

49. Логарифмический вычет

Опр: пусть функция f(z) голоморфна в проколотой окрестности т. а и не обращ. в 0 в этой окрестности. Логарифмическим вычетом функции f(z) в т. а называется вычет функции

f′(z)/f(z) в т. а.( )

Т еорема (о логарифмическом вычете): пусть D – ограниченная обл. с кусочно-гладкой границей. Пусть f(z) голоморфна в D и непрерывна вD за искл. конечного числа полюсов, лежащих в D и пусть f(z) имеет вD конечное число нулей, лежащих в D. Тогда

N- число нулей f(z) в обл. D, P – число полюсов f(z) в обл. D, причем нули и полюса считаются столько раз, какова их кратность.

Док-во:

a₁,…,a_k – нули f(z), b₁,…,b_l – полюса f(z) лежат в D, но не на D.

f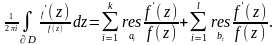 (z)/f(z) – имеет особенности только в точках a₁,…,a_k, b₁,…,b_l . Тогда:

1) пусть а – ноль f(z) порядка n, в окр. т.а f(z)=(z-a)ⁿ(z).

(z) – голоморфна в окр. т.а, (а)≠0.

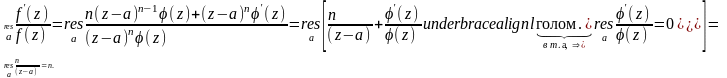
2) пусть b – полюс f(z) кратности р, в окр. т.b f(z)= (z)/(z-b)^p, где (z) – голоморфна в окр. т.b, (b)≠0.

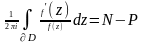
Суммируя все вычеты получаем: 

53. Вычет относительно бесконечно удаленной точки.

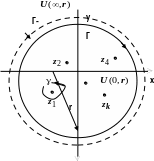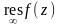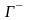Д ля конечной особой точки , где - контур, не содержащий других, кроме , особых точек, проходимый так, что область, им ограниченная и содержащая особую точку, остаётся слева (против часовой стрелке). Определим аналогичным образом: , где - контур, ограничивающий такую окрестность 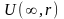точки , которая не содержит других особых точек, и проходимый так, что эта окрестность остаётся слева (по часовой стрелке). Таким образом, все остальные (конечные) особые точки функции должны находиться внутри контура . Изменим направление обхода контура : 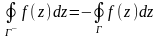. По основной теореме о вычетах 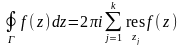, где суммирование ведётся по всем конечным особым точкам. Поэтому, окончательно, 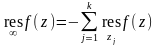, т.е. вычет в бесконечно удалённой особой точке равен сумме вычетов по всем конечным особым точкам, взятой с противоположным знаком.

53. Теорема о сумме вычетов.

вычет в бесконечно удалённой особой точке равен сумме вычетов по всем конечным особым точкам, взятой с противоположным знаком. Как следствие, имеет место теорема о полной сумме вычетов: если функция аналитична всюду в плоскости С, за исключением конечного числа особых точек 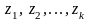, то сумма вычетов во всех конечных особых точках и вычета в бесконечности равна нулю.

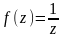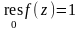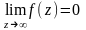Отметим, что если - устранимая особая точка, то вычет в ней может быть отличен от нуля. Так для функции , очевидно, ; - единственная конечная особая точка этой функции, поэтому , несмотря на то, что , т.е. - устранимая особая точка.