
- •Множества, области, кривые.
- •Комплексная плоскость.
- •Односвязные и многосвязные области.
- •Последовательности комплексных чисел.
- •Предел последовательности комплексных чисел.
- •6.Понятие функции комплексной переменной.
- •7.Предел и непрерывность функции комплексной переменной.
- •8.Основные элементарные функции комплексной переменной.
- •9.Определение производной. Дифференцирование функции комплексной переменной.
- •10.Дифференциал. Условия Коши-Римана.
- •Аналитическая функция.
- •Гармонические функции. Сопряженно-гармонические функции.
- •13.Геометрический смысл модуля производной. Коэффициент подобия.
- •14. Геометрический смысл аргумента производной.
- •Понятие о конформном отображении.
- •Конформное отображение 1-го рода. Конформное отображение 2-го рода.
- •Критерий конформности.
- •Принцип взаимно-однозначного соответствия границ.
- •Принцип симметрии Римана-Шварца. Примеры функций, задающих конформное отображение
- •Определение интеграла от функции комплексной переменной.
- •21.Связь интеграла комплексной переменной с криволинейным интегралом 2-го рода.
- •22.Свойства интеграла от фкп.
- •Оценка интеграла от функции комплексной переменной.
- •Основная теорема Коши. Теорема Коши для многосвязной области.
- •Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница.
- •Интеграл Коши.
- •27.Теорема о среднем для аналитических функций.
- •Принцип максимума модуля аналитической функции.
- •Интеграл типа Коши
- •Теорема Коши-Лиувилля.
- •Теорема Морера.
- •Числовые ряды с комплексными членами. Частичная сумма ряда.
- •Необходимое и достаточное условия сходимости числового ряда.
- •Функциональные ряды. Точка сходимости. Область сходимости.
- •Равномерная сходимость функциональных рядов.
- •Степенные ряды. Круг и радиус сходимости степенного ряда.
- •Ряд Тейлора. Разложение в ряд Тейлора некоторых элементарных функций комплексной переменной.
- •Формулы Эйлера.
- •Голоморфные функции.
- •Нули аналитической функции.
- •Ряд Лорана. Область сходимости ряда Лорана.
- •Разложение аналитической функции в ряд Лорана.
- •Классификация изолированных особых точек аналитической функции.
- •Устранимая особая точка.
- •Полюс. Порядок полюса.
- •Существенно особая точка.
- •Теорема Сохотского.
- •Разложение аналитической функции в ряд Лорана в окрестности бесконечно удаленной точки.
- •Понятие вычета. Основная теорема о вычетах.
- •Вычисление вычетов для простого полюса.
- •Вычисление вычетов для полюса порядка n.
- •Логарифмический вычет
- •Вычет относительно бесконечно удаленной точки.
- •Теорема о сумме вычетов.
- •Вычисление интегралов по замкнутому контуру.
- •Вычисление с помощью вычетов определенных интегралов от рациональных функций действительной переменной
- •Вычисление с помощью вычетов определенных интегралов от тригонометрических функций.
- •58.Вычисление с помощью вычетов несобственных интегралов от функций
- •Лемма Жордана.
- •Суммирование некоторых рядов с помощью вычетов Формула суммирования знакопеременного ряда с рациональными слагаемыми.
Ряд Лорана. Область сходимости ряда Лорана.
Ряд
Лорана. Пусть
функция
аналитична в кольце
 .
Тогда для любой точки этого кольца
.
Тогда для любой точки этого кольца
 ;
при этом окружности проходятся так, что
область остаётся слева. Изменим в
интеграле по внутренней окружности
направление обхода на противоположное:
;
при этом окружности проходятся так, что
область остаётся слева. Изменим в
интеграле по внутренней окружности
направление обхода на противоположное:
 .
Интеграл по внешней окружности преобразуем
так, как и при выводе формулы Тейлора:
(так
как
,
то
)
,
и ряд сходится абсолютно, поэтому его
можно почленно интегрировать:
.
Интеграл по внешней окружности преобразуем
так, как и при выводе формулы Тейлора:
(так
как
,
то
)
,
и ряд сходится абсолютно, поэтому его
можно почленно интегрировать:
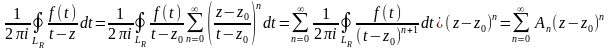 ,
где
,
где
 .
Интеграл по внутренней окружности
преобразуем аналогично, учитывая только,
что на
.
Интеграл по внутренней окружности
преобразуем аналогично, учитывая только,
что на
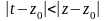 :
:

 .
И здесь ряд сходится абсолютно, поэтому
его можно почленно интегрировать:
.
И здесь ряд сходится абсолютно, поэтому
его можно почленно интегрировать:
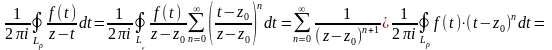
 ,
где
,
где
 .
Переобозначим
.
Переобозначим
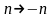 ,
тогда форма коэффициентов ряда для
совпадёт с формой коэффициентов ряда
для
:
,
тогда форма коэффициентов ряда для
совпадёт с формой коэффициентов ряда
для
:
 поэтому окончательно для интеграла по
получим
поэтому окончательно для интеграла по
получим
 .
Докажем, что и контур для вычисления
коэффициентов может быть взят один и
тот же. Действительно, пусть
.
Докажем, что и контур для вычисления
коэффициентов может быть взят один и
тот же. Действительно, пусть
 - кусочно-гладкий контур, расположенный
в кольце
,
и точка
расположена внутри этого контура. По
теореме Коши для многосвязной области
- кусочно-гладкий контур, расположенный
в кольце
,
и точка
расположена внутри этого контура. По
теореме Коши для многосвязной области
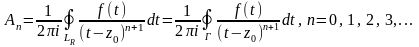 ;
;
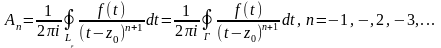 ,
поэтому для любого n
,
поэтому для любого n
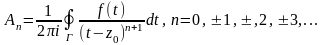 ,
и
,
и
 .
.
Этот ряд (содержащий
и положительные, и отрицательные степени
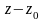 ),
называется рядом Лорана функции
.
Его часть, содержащая неотрицательные
степени (
),
называется рядом Лорана функции
.
Его часть, содержащая неотрицательные
степени ( ),
называется правильной; часть, содержащая
отрицательные степени (
),
называется правильной; часть, содержащая
отрицательные степени (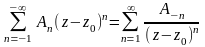 ),
называется главной. Правильная часть,
по самому своему построению, сходится
в круге
),
называется главной. Правильная часть,
по самому своему построению, сходится
в круге
 ,
главная - во внешности круга
,
главная - во внешности круга
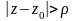 ,
поэтому весь ряд сходится в пересечении
этих областей, т.е. в кольце
,
поэтому весь ряд сходится в пересечении
этих областей, т.е. в кольце
 .
Так же, как и для ряда Тейлора, разложение
в ряд Лорана единственно.
.
Так же, как и для ряда Тейлора, разложение
в ряд Лорана единственно.
Еще раз подчеркнем, что в ряд Лорана раскладывается функция, аналитическая в кольце, и ширина этого кольца определяется областью аналитичности функции, т.е. разложение теряет смысл, как только функция теряет аналитичность.
Разложение аналитической функции в ряд Лорана.
в ряд Лорана раскладывается функция, аналитическая в кольце, и ширина этого кольца определяется областью аналитичности функции, т.е. разложение теряет смысл, как только функция теряет аналитичность. Рассмотрим
Пример 1.
Требуется получить все возможные
разложения в ряд Лорана по степеням
 функции
функции
 .
.
Здесь
 ;
функция теряет аналитичность в точках
;
функция теряет аналитичность в точках
 .
Легко видеть, что существует три области
аналитичности с центром в
(один круг и два кольца), на границах
которых функция теряет аналитичность:
.
Легко видеть, что существует три области
аналитичности с центром в
(один круг и два кольца), на границах
которых функция теряет аналитичность:
1.
 ;
2.
;
2.
 ;
3.
;
3.
 .
В каждой из этих областей разложение
будет таким:
.
В каждой из этих областей разложение
будет таким:
1.
В первой области (круге) функция
аналитична, поэтому ряд Лорана будет
совпадать с рядом Тейлора.
 - таково разложение
на простые дроби, разлагаем в ряд Тейлора
каждую их них.
- таково разложение
на простые дроби, разлагаем в ряд Тейлора
каждую их них.
 ,
где
;
,
где
;
 ;
это разложение справедливо, если
;
это разложение справедливо, если
 ,
т.е. в первой и второй областях. Окончательно
в первой области
,
т.е. в первой и второй областях. Окончательно
в первой области
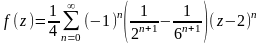 .
Этот ряд содержит только правильную
часть.
.
Этот ряд содержит только правильную
часть.
2. В кольце
знаменатель второй геометрической
прогрессии (для дроби
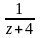 )
по модулю
)
по модулю
 ,
поэтому разложение остаётся в силе. Для
первой дроби, с учётом того, что
,
поэтому разложение остаётся в силе. Для
первой дроби, с учётом того, что
 ,
получим
,
получим
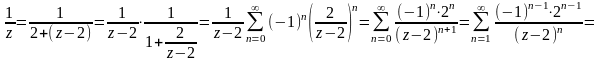 =
= .
Это - главная часть ряда Лорана. Разложение
имеет вид
.
Это - главная часть ряда Лорана. Разложение
имеет вид
 .
.
3. В кольце
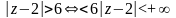 для первой дроби получим разложение
так:
для первой дроби получим разложение
так:
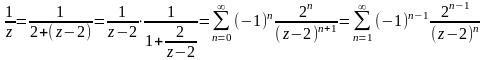 или
или
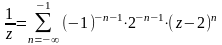 .
Для второй дроби
.
Для второй дроби
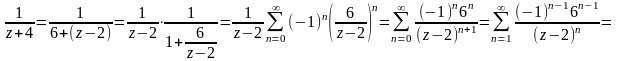
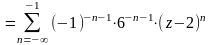 .
Ответ можно записать и в форме
.
Ответ можно записать и в форме
 ,
и в форме
,
и в форме
 .
В этом разложении имеется только главная
часть.
.
В этом разложении имеется только главная
часть.
