7.2.2 Графическое представление сетевой модели
На основании таблицы 1 построим граф сетевой модели (рис. 1)
2
7
1
9
3
5
6
10
11
4
8
13
12
Рис. 1. Сетевая модель
Построенный граф состоит из тринадцати событий (вершины графа) и шестнадцати работ (дуги графа). На дугах может быть указана продолжительность соответствующих им работ (на рис.1 она опущена).
Единственное событие, наступающее без предшествующих ему работ — событие «начало работ», помеченное номером «0».
«Окончание работ» — событие номер «13» не имеет работ, начинающихся с него.
Для корректности дальнейшего расчёта необходимо, чтобы в графе событие с номером i не зависело от событий с номерами, большими, чем i. Если такие случаи есть, необходимо перенумеровать события, чтобы исключить их. Как видно из графа сетевой модели (рис. 1), это условие соблюдено (ни одна дуга не выходит из вершины с большим номером в вершину с меньшим). Жирной линией на схеме (рис. 1) выделен критический путь (см. ниже п.п. 7.2.3, 7.2.4).
7.2.3 Расчёт показателей сетевой модели
Показатели сетевой модели позволяют определить продолжительность, сроки выполнения и степень напряженности всего комплекса работ в целом и каждой работы в отдельности, а также принять решение о перераспределении ресурсов.
Для всех работ рассчитаем следующие показатели:
Ранний срок начала работы:
Ранний срок окончания работы:
Поздний срок начала работы:
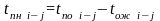
Поздний срок окончания работы:
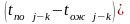
Полный резерв времени:
Свободный резерв времени:
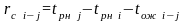
Результаты занесём в таблицу 2:
Таблица 2. Расчёт параметров сетевой модели
Код работы |
, дней |
Ранний срок |
Поздний срок |
Резервы |
кр. путидней |
кр. пути дней |
|||||
|
|
|
|
|
|
||||||
1 |
2 |
3 |
4 = 2 + 3 |
5 = 6 – 2 |
6 |
7 = 5 – 3 |
8 |
9 |
10 |
||
0 — 1 |
3,4 |
0 |
3,4 |
0 |
3,4 |
0 |
0 |
3,4 |
0,04 |
||
1 — 2 |
5,8 |
3,4 |
9,2 |
12,8 |
18,6 |
9,4 |
0 |
0 |
0 |
||
1 — 3 |
6,2 |
3,4 |
9,6 |
3,4 |
9,6 |
0 |
0 |
6,2 |
0,36 |
||
1 — 4 |
8,2 |
3,4 |
11,6 |
7,2 |
15,4 |
3,8 |
3,8 |
0 |
0 |
||
1 — 5 |
15,2 |
3,4 |
18,6 |
4,0 |
19,2 |
0,6 |
0,6 |
0 |
0 |
||
2 — 5 |
1,4 |
9,2 |
10,6 |
17,8 |
19,2 |
8,6 |
8,6 |
0 |
0 |
||
3 — 4 |
5,8 |
9,6 |
15,4 |
9,6 |
15,4 |
0 |
0 |
5,8 |
0,16 |
||
4 — 5 |
3,8 |
15,4 |
19,2 |
15,4 |
19,2 |
0 |
0 |
0 |
0 |
||
5 — 6 |
13,2 |
19,2 |
32,4 |
19,2 |
32,4 |
0 |
0 |
13,2 |
0,36 |
||
6 — 7 |
11,2 |
32,4 |
43,6 |
33,6 |
44,8 |
1,2 |
0 |
0 |
0 |
||
6 — 8 |
15,2 |
32,4 |
47,6 |
32,4 |
47,6 |
0 |
0 |
15,2 |
0,36 |
||
6 — 9 |
15,8 |
32,4 |
48,2 |
35,2 |
51,0 |
3,0 |
2,8 |
0 |
0 |
||
7 — 8 |
2,8 |
43,6 |
46,4 |
44,8 |
47,6 |
1,2 |
1,2 |
0 |
0 |
||
8 — 9 |
3,4 |
47,6 |
51,0 |
47,6 |
51,0 |
0 |
0 |
3,4 |
0,04 |
||
9 — 10 |
7,8 |
51,0 |
58,8 |
51,0 |
58,8 |
0 |
0 |
7,8 |
0,16 |
||
10 — 11 |
15,2 |
58,8 |
74,0 |
58,8 |
74,0 |
0 |
0 |
15,2 |
0,36 |
||
11 — 12 |
9,8 |
74,0 |
83,8 |
74,0 |
83,8 |
0 |
0 |
9,8 |
0,16 |
||
12 — 13 |
2,4 |
83,8 |
86,2 |
83,8 |
86,2 |
0 |
0 |
2,4 |
0,04 |
||
Суммарные время и дисперсия критического пути: |
86,2 |
2,04 |
|||||||||
,
дней
,
дней
,
дней
,
дней
,
дней
,
дней