20. Градиентные методы поиска экстремума. Метод Ньютона.

В методе Коши применяется наилучшая локальная стратегия поиска точки с использованием градиента, однако движение в напр противоположном градиенту приводит в точку min, лишь в том случает, когда линии равного уровня функцf(x) представляет собой окружности. Т.о. напрпротивоположgrad не может служить приемлемым глобальным направлением поиска точек оптимума нелин функции.

Для того чтобы построить более общ стратегию поиска, необходимо привлечь инф не только о первых, но и о вторых переменных целевой функции. В методе Ньютона стратегия поиска строится на основе разложения целевой функции в ряд Тейлора, в котором все челены разложения выше второго порядка отбрасываются.

Н

а основе этой аппроксимациипостр последовательность итераций, чтобы во вновь полученной точке х(к+1) gradфункц обращался в ноль.

,

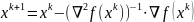где

Пример: