7. Выборочное распределение для оценки дисперсии
Распределение величины S2 задается χ2 – распределением.
оценка
Графически распределение χ2-статистикиимеет вид:
Распределение χ2 задается таблицами вероятности(получить расчетное значениеχ2>табличное).
ν Р |
0,99 |
0,95 |
0,9 |
… |
0,05 |
0,025 |
0,01 |
|
|
|
|
|
|
|
|
8. Применение выборочных распределений для интервального оценивания параметров систем управления.(нужно также в этом билете кратко рассказать 9,10, 11- все что связано с интервалами)
Если представляет собой оценку истинного значения параметра β, то зная выборочное распределение , можно найти такие два числа δ1, δ2 для которых выполняется условие:
9.Доверительный интервал генерального среднего
Для построения доверительного интервала используют t – статистику
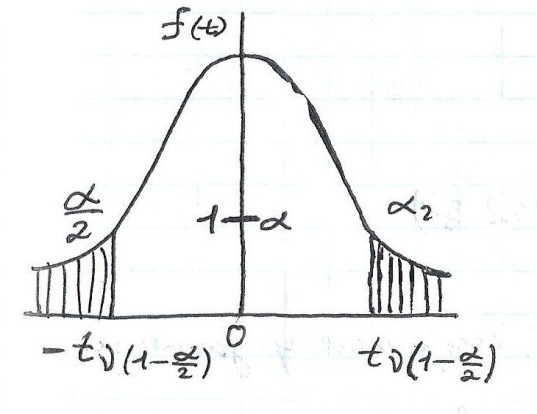
Числовой пример
Пусть выборка из n=10 измерений
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
yi |
68 |
50 |
45 |
75 |
39 |
62 |
48 |
45 |
50 |
45 |
n=10;
=9
;
Зададим
доверительность вероятностьюР= 0,95
следовательно уровнем значимости
α=0,05;
Для вероятности 0,975 и =9
T9;0,975=2,262
Таким образом, доверительный интервал:
(52-2,262·3,1; 52+2,262·3,1)
Следовательно с вероятностью Р=0,95, истинное среднее значение рассматриваемой случайной величины будет находиться в пределах:
10. Доверительный интервал для генеральной дисперсии.
Для
определения доверительного интервала
генеральной дисперсии используют
-статистику.
Т
.к.
таблица задает вероятность того, что
Х2расп>X2табл,
можно записать:
;
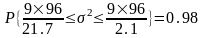
На практике часто приходится решать обратную задачу: по истинному значению ср. величины и требуемой точности найти требуемое число экспериментов для обеспечения этой точности.
σ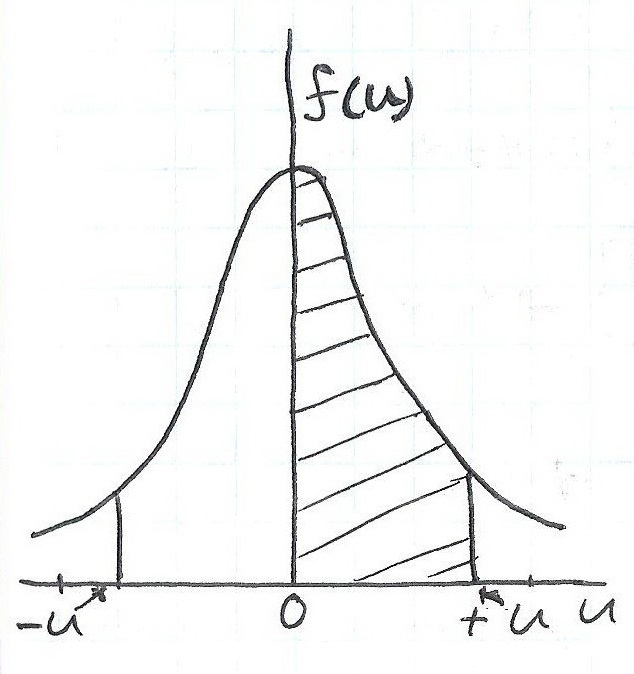
2Х=0,01
(σ=0,1)
±0,02 Р=0,95
n - ?
Известно, что генеральная совокупность исследуемых случайных величин распространяется нормально. Для решения такой задачи можно использовать выборочное распределение для ср. значения и дисперсии.
11. Определение объема выборки, который позволит с вероятностью Р=0,95 накрыть истинное значение дисперсии доверительным интервалом шириною 0,1σ2.
Определим объем выборки, для которой доверительный интервал 0,1σ2 будет накрывать истинное значение дисперсии с вероятностью 0,95.
