Вопрос 1

Множественная линейная регрессия является обобщением парной линейной регрессии на несколько объясняющих переменных. При выполнении предпосылок Гаусса-Маркова оценки параметров уравнения множественной линейной регрессии, полученные методом наименьших квадратов, обладают свойствами несмещенности, эффективности и состоятельности. Статистическая значимость коэффициентов и качество подбора уравнения проверяются с помощью распределений Стьюдента и Фишера. Коэффициент при объясняющей переменной показывает, на сколько единиц изменится зависимая переменная, если объясняющая вырастет на одну единицу при фиксированном значении остальных объясняющих переменных. В случае множественной регрессии дополнительно предполагается отсутствие мультиколлинеарности объясняющих переменных.

Вопрос 2

В основе метода наименьших квадратов (МНК) лежит поиск таких значений коэффициентов регрессии, при которых сумма квадратов отклонений теоретического распределения от эмпирического была бы наименьшей.

Оценки коэффициентов моделей, полученные на основе МНК, не зависят от фактического закона распределения.

В отношении свойств ошибки модели выдвигаются следующие предположения:

– ошибка имеет нулевое математическое ожидание;

– ее дисперсия конечна и постоянна;

– автокорреляционные связи в ряду ошибки отсутствуют

– ряд значений ошибки статистически не связан с рядами значений независимых переменных модели.

3. Геометрическая интерпретация мнк

Геометрически задача МНК состоит в том, чтобы найти такой вектор у^ из £(Х), чтобы евклидово расстояние между у и у^ было минимальным. Иными словами, мы ищем среди всех линейных комбинаций регрессоров наиболее близкую к y.

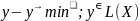
4.Теорема Гаусса-Маркова

Если предпосылки метода наименьших квадратов, то оценки, полученные по МНК, обладают следующими свойствами:

1. Оценки параметров являются несмещенными, т. е. M(b₁) = β₁, M(b₀) = β₀ (математические ожидания оценок параметров равны их теоретическим значениям). Это вытекает из того, что M(ε_i) = 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2. Оценки параметров состоятельны, так как дисперсия оценок параметров при возрастании числа n наблюдений стремится к нулю D(b₀) → 0, D(b₁) → 0 при n → ∞ . По другому говоря, при увеличении объема выборки надежность оценок увеличивается (b₁ наверняка близко к β₁, b₀ — близко к β₀).

3. Оценки параметров эффективны, т. е. они имеют наименьшую дисперсию по сравнению с другими оценками данных параметров, линейными относительно величин y_i.

Предпосылки МНК (Условия Гаусса-Маркова):

1. Математическое ожидание случайного отклонения е_i равно нулю: M(е_i) = 0 для всех наблюдений.

2. Дисперсия случайных отклонений epsiloni постоянна: D(εi) = D (εj ) = σ² = const для любых наблюдений i и j.

3. Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j.

4. Случайное отклонение должно быть независимо от объясняющих переменных.

5. Модель является линейной относительно параметров.

6. Отсутствие мультиколлинеарности.

7. Случайные отклонения εi, i = 1, 2, ... , n, имеют нормальное распределение.