48. Параметрические уравнения прямой. Угол между прямыми в .

Параметрические уравнения прямой в пространстве:

Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем. В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t0=0 он находится в точке М0, в любой другой момент времени t его координаты в пространстве вычисляются по формулам. Теперь несколько преобразуем формулы . Выразим из каждой строчки параметр t:

49.Окужность и эллипс. Уравнение эллипса. Эксцентриситет эллипса.

Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек MЕ вклидовой плоскости, для которых сумма расстояний до двух данных точек   и   (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

 причем 

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

Каноническое уравнение эллипса может быть параметризовано:

где   — параметр уравнения.

В случае окружности параметр   является углом между радиус-вектором данной точки и положительным направлением оси абсцисс.

В полярных координатах

Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах   будет иметь вид

где e — эксцентриситет, а p — фокальный параметр. При положительном знаке перед e второй фокус эллипса будет находиться в точке   а при отрицательном — в точке   где фокальное расстояние 

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .

е = с/ a .

Т.к. с < a , то е < 1.

 

Определение. Величина k = b / a называется коэффициентом сжатия , а величина 1 – k = ( a – b )/ a называется сжатием.

Коэффициент сжатия и эксцентриситет связаны соотношением: k² = 1 – e ² .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х ₁ , у ₁ ) выполняется условие:  , то она находится внутри эллипса, а если  , то точка находится вне его.

Теорема. Для произвольной точки М(х, у), принадлежащей фигуре эллипс верны соотношения :

r ₁ = a – ex , r₂ = a + ex .

 

Доказательство. Выше было показано, что r₁ + r₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

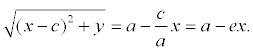
Аналогично доказывается, что r₂ = a + ex . Теорема доказана.