45. Уравнение прямой в , проходящей через точку перпендикулярно вектору.

Требуется составить уравнение прямой, проходящей через точку   перпендикулярно вектору  .

Выберем на плоскости произвольную точку  . Обозначим   и   — радиус-векторы точек   и  . Точка   принадлежит заданной прямой тогда и только тогда, когда векторы   и   перпендикулярны (рис.3.5,б). Условие ортогональности запишем при помощи скалярного произведения:

Учитывая, что  , получаем векторное уравнение прямой:

(3.5)

Это уравнение можно записать в другой форме. Преобразуем левую часть , используя свойства скалярного произведения. Обозначая  , получаем уравнение

(3.6)

выражающее постоянство проекций на нормаль   радиус-векторов точек, принадлежащих прямой.

Получим координатную форму записи векторного уравнения прямой (3.5). Так как   и  , по формуле (1.9) находим   или

(3.7)

Полученное соотношение (3.7) позволяет по координатам точки   и координатам  нормали   записать уравнение прямой без промежуточных вычислений.

46. Уравнение прямой, проходящей через две точки. Уравнение прямой в , в отрезках на осях координат.

Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂ .

Дробь 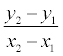 = k называется угловым коэффициентом прямой.

     (3)

где a - величина отрезка, отсекаемого прямой на оси Ox; b - величина отрезка, отсекаемого прямой на оси Oy.

Каждый из этих отрезков отложен от начала координат.

Особенности этого уравнения такие: в левой части уравнения между дробями сосит знак плюс, величины a и b могут быть как положительными, так и отрицательными, правая часть уравнения равна единице.

47. Нормальное уравнение прямой. Расстояние от данной точки до данной прямой.

1. Нормальное уравнение прямой

где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а   - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель  , взятый со знаком, противоположным знаку свободного члена C.

2. Расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

Правило. Чтобы определить расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:

Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой.

Отклонение   данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.

Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.