2.2. Ряд Фур'є для періодичних сигналів [1, с. 27-31]

2.2.1. Форми запису ряду Фур'є

Сигнал називається періодичним, якщо його форма циклічно повторюється через певний відрізок часу. Періодичний сигнал у загальному виді записується як.

, m=0, 1, 2, …, (2.2)

де Т – період сигналу.

Для математичного опису періодичних сигналів можна користуватись рядом (2.2), в якому як базисні функції зручно вибрати гармонічні (синусоїдні і косинусоїдні) функції (коливання) кратних частот

; ; ; ; ; …; (2.3)

де 1=2/Т – основна кутова частота цих функцій.

2.2.2. Спектральна діаграма і спектр періодичного сигналу

Якщо будь-який сигнал представлений як сума гармонічних коливань з різними частотами, то кажуть, що здійснено спектральний розклад сигналу.

Спектр сигналу – це сукупність гармонічних складових із конкретними значеннями частот, амплітуд і початкових фаз, які при додаванні дають цей сигнал.

Спектральною діаграмою сигналу прийнято називати графічне зображення коефіцієнтів ряду Фур'є цього сигналу. Спектральних діаграм для кожного сигналу існує дві: амплітудна та фазова. У деякому масштабі ці діаграми показано на рис. 2.6, де на горизонтальній осі відкладені значення частот гармонік, на вертикальній – їх амплітуди Аmn і фази n. Зазначимо, що амплітуди гармонік приймають тільки додатні, фази – як додатні, так і від'ємні значення в інтервалі –n+.

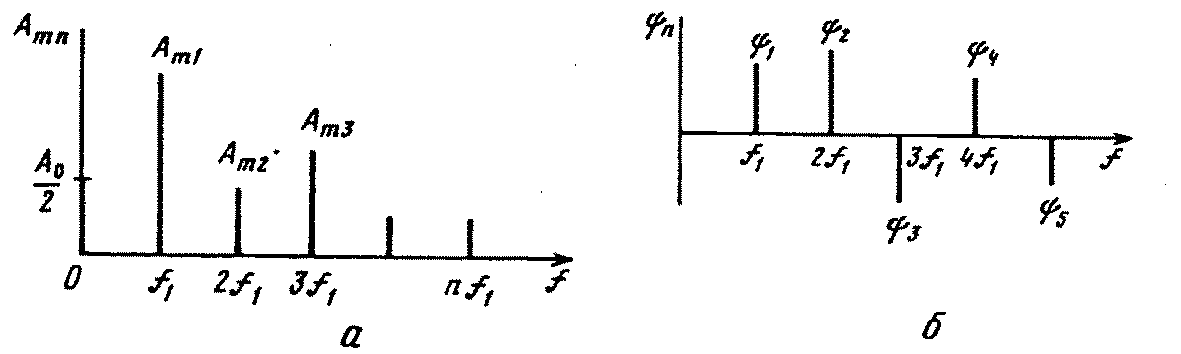
Рис. 2.6. спектральні діаграми періодичного сигналу:

а – амплітудна; б - фазова

Часто в технічній літературі спектральні діаграми називають більш коротко – амплітудний спектр, фазовий спектр. Найчастіше цікавляться амплітудним спектром, через те, що на ньому добре видно розподіл гармонічних складових у спектрі. Зазначимо, що спектр періодичного сигналу є дискретним, тобто має складові на дискретних частотах.

3. Кодування сигналів, аналого-цифрове перетворення

3.1. Ряд і теорема Котельникова [1, с. 34-40]

3.1.1. Розкладання неперервних сигналів у ряд Котельникова

Всі реальні неперервні сигнали є плавними функціями часу. Стрибки миттєвих значень у них практично відсутні. Тому такі сигнали можна представити послідовністю їх миттєвих значень, які взято через деякий інтервал часу t. Миттєве значення сигналу у фіксований момент часу tк називається відліком і позначається u(tк), а інтервал часу t – кроком дискретизації.

Виникає запитання: як часто необхідно брати відліки, щоб за ними можна було відновити сигнал? Відповідь дає доведена в 1933 р. академіком В.О. Котельниковим теорема, яка і носить його ім'я. Згідно з цією теоремою, будь-який неперервний сигнал u(t), що не має частот вище за Fmax, можна точно відновити за його відліками u(kt), які взято через інтервал (крок) дискретизації t=l/(2Fmax). Це відновлення здійснюється за допомогою ряду

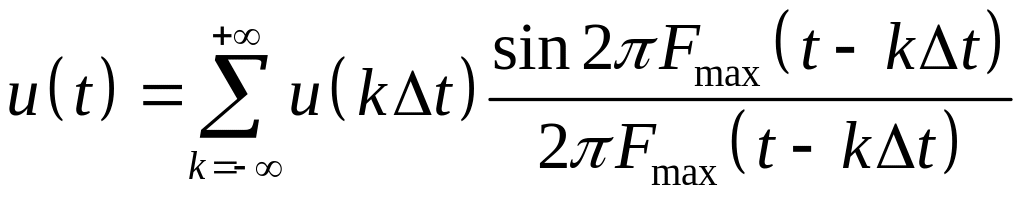(2.15)

Ряд, що подано виразом (2.15), називається рядом Котельникова.

Теорема Котельникова є основою для дискретизації неперервних сигналів за часом. У ній, по-перше, доводиться, що неперервний сигнал можна замінити його миттєвими значеннями (відліками), по-друге, вона дає правило знаходження кроку дискретизації - t=l/(2Fmax) При такому кроці дискретизації ряд Котельникова дає точне часове подання складного сигналу.

Інколи виникає запитання, яким рядом (Фур'є чи Котельникова) краще користуватись для математичного опису складного сигналу? Певної відповіді дати неможливо – це залежить від конкретної задачі. Єдине, що можна певно зазначити, так це простоту розрахунків коефіцієнтів розкладу a_к у ряді Котельникова (вони є відліками сигналу u(kt) через інтервал kt).