4.2.10. Абсолютная и относительная адресация
При работе с формулами значение выражения зависит от содержимого ячеек, ссылки на которые используются в формуле.
Основное свойство электронной таблицы: изменение числового значения в ячейке приводит к мгновенному пересчету формул, содержащих ссылку на эту ячейку.
Ссылки могут быть абсолютные, относительные и смешанные.
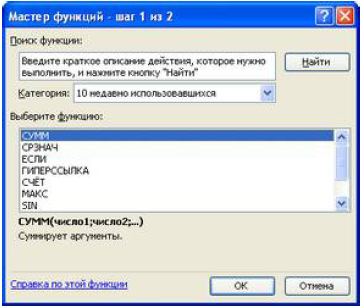
Рис. 4.4. Окно Мастер функций
По умолчанию для указания адресов ячеек создаются относительные ссылки. Это означает, что ссылки на ячейки изменяются при перемещении формулы на новое место.
Относительная ссылка указывает на ячейку, основываясь на ее положении относительно ячейки, в которой находится формула. После копирования формулы относительные ссылки будут указывать на другие ячейки. Например, формула =A3+B3, хранящаяся в ячейке С3, при перемещении в ячейку С4 примет вид: =A4+B4.
В тех случаях, когда ссылки не должны изменяться при копировании формулы, следует использовать абсолютные ссылки. Абсолютные ссылки обозначаются знаком доллара, например $A$4.
Ссылки вида $A4 или A$4 называются смешанными. Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка столбцов приобретает вид $A4, $B4 и т. д. Абсолютная ссылка строки приобретает вид A$4, B$4 и т. д. При изменении позиции ячейки, содержащей формулу, относительная ссылка изменяется, а абсолютная ссылка не изменяется. При копировании формулы вдоль строк и вдоль столбцов относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании смешанной ссылки из ячейки A2 в ячейку B3, она изменяется с =A$1 на =B$1.
4.3. Порядок выполнения работы
Данная лабораторная работа предполагает выполнение следующих этапов:
1. Изучить методические указания к лабораторной работе
2. Пройти собеседование с преподавателем и получить задание для выполнения работы
3. На листе 1 создать ведомость, образец которой показан в табл. 4.2 (ячейки, в которых значения должны быть найдены через формулы отмечены серым цветом).
Формулы для нахождения суммарного расхода и прибыли имеют следующий вид:
Суммарный расход = Зарплата + Закупка материалов + Накладные расходы
Прибыль = Доход от продажи – Суммарный расход.
Таблица 4.2
Ведомость о балансе предприятия за 2010 г.
Месяц |
Зарплата |
Закупка материалов |
Накладные расходы |
Доход от продажи |
Суммарный расход |
Прибыль |
Январь |
|
|
|
|
|
|
Февраль |
|
|
|
|
|
|
Март |
|
|
|
|
|
|
Апрель |
|
|
|
|
|
|
Май |
|
|
|
|
|
|
Июнь |
|
|
|
|
|
|
Июль |
|
|
|
|
|
|
Август |
|
|
|
|
|
|
Сентябрь |
|
|
|
|
|
|
Октябрь |
|
|
|
|
|
|
Ноябрь |
|
|
|
|
|
|
Декабрь |
|
|
|
|
|
|
Макс. за год |
|
|
|
|
|
|
Мин. за год |
|
|
|
|
|
|
Сред. за год |
|
|
|
|
|
|
Итого |
|
|
|
|
|
|
4. Составить таблицу значений функции двух переменных F(x, y), заданной в прямоугольной области [a, b]×[c, d], для аргументов xi = a + i∙hx, yj = c + j∙hy, где i = 0…Nx, j = 0…Ny,
, 
.
Исходные данные для выполнения задания взять из табл. 4.3.
5. Оформить и защитить отчет по лабораторной работе.
Таблица 4.3
Варианты заданий
№ |
F(x, y) |
A |
b |
c |
d |
hx |
hy |
1 |
xy + 5,6(x + y) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
2 |
ln(x + y) |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
3 |
cos(x) + sin(y) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
4 |
sin(x) + cos(y) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
5 |
tg(x + y) |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
6 |
sin(x) + xy |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
7 |
cos(x) + 5xy |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
8 |
y + tg(x + y) |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
9 |
sin(xy) + cos( |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
10 |
5sin(cos(x + y) + 3,78) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
11 |
6,4cos(5,8 + ln(xy)) |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
12 |
xy + x2 + y2 |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
13 |
sin2(x + y) + cos2(x + y) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
14 |
xsin(y) + ycos(x) |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
15 |
10xy(sin(xy) + cos(y)) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
16 |
xy – 5,6(x – y) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
17 |
xyln(x + y) |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
18 |
xy(cos(x) + sin(y)) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
19 |
x(sin(x) + cos(y)) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
20 |
xytg(x + y) |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
21 |
sin(x) + xy – 2 |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
22 |
cos(x) + 5xy – sin(y) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
23 |
xy + tg(x + y) – 4 |
1 |
3 |
0 |
2 |
0,2 |
0,2 |
24 |
xy(sin(xy) + cos(xy)) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
25 |
xysin(cos(x + y) + 3,78) |
0 |
1 |
0 |
1 |
0,1 |
0,1 |
4.4. Контрольные вопросы
1.
2.
3.
4.
5.
5. РАБОТА С ДИАГРАММАМИ И ЛОГИЧЕСКИМИ ФУНКЦИЯМИ В MS EXCEL
5.1. Цель работы
Цель работы – приобрести умение работать с диаграммами и логическими функциями в MS Excel.
5.2. Основные теоретические сведения
5.2.1. Общие сведения о диаграммах Excel
Диаграмма Excel – это наглядное графическое представление различных данных, удобное средство сравнения и демонстрации. Для создания диаграммы необходимо использовать данные, расположенные на листе. При этом диаграмма связана со значениями и будет автоматически обновляться при их изменении в таблице.
Для отображения числовых данных, введенных в ячейки таблицы, используются линии, полосы, столбцы, сектора и другие визуальные элементы. Диаграмму можно отобразить как в виде отдельного листа книги, так и поместить на лист с данными подобно рисунку или автофигуре.
Все диаграммы Excel, за исключением круговой, имеют две оси: горизонтальную – ось категорий и вертикальную – ось значений. При создании объёмных диаграмм добавляется третья ось – ось рядов.
Часто диаграмма содержит такие элементы, как сетка, заголовки и легенда. Линии сетки являются продолжением делений, находящихся на осях, заголовки используются для пояснений отдельных элементов диаграммы и характера представленных на ней данных, легенда помогает идентифицировать ряды данных, представленные на диаграмме.
Можно выделить следующие основные типы диаграмм:
1). Гистограммы, которые, как правило, используются для отображения изменений данных за определенный период времени или для сравнения различных объектов. При этом категории в них обычно формируются по горизонтальной оси, а значения – по вертикальной.
2). Графики, которые позволяют демонстрировать непрерывную зависимость значений одной переменной от другой.
3). Круговые диаграммы, которые отображают величину размера элементов одного ряда данных пропорционально сумме всех элементов.
4). Линейчатые диаграммы, которые отображают явное сравнение отдельных элементов.
5). Кольцевые диаграммы, которые подобно круговой диаграмме иллюстрируют отношение частей к целому, но при этом могут содержать более одного ряда данных.
Добавлять диаграммы можно двумя способами: внедрять их в текущий рабочий лист и добавлять отдельный лист диаграммы. В том случае, если интерес представляет сама диаграмма, то она размещается на отдельном листе. Если же нужно одновременно просматривать диаграмму и данные, на основе которых она была построена, то тогда создаётся внедрённая диаграмма.
Для того чтобы вставить диаграмму необходимо выполнить следующие действия:
1. На рабочем листе выделяются ячейки, содержащие данные, которые следует представить в виде диаграммы. Также выделяются описания данных, которые будут использоваться для легенды на диаграмме.
2. На вкладке Вставка в группе Диаграммы раскрывается меню нужного типа диаграммы (гистограмма, круговая, график и т. д.) .
3. В списке команд выбирается нужная разновидность выбранного типа диаграммы.