
- •Билет № 1
- •Билет № 2
- •Билет № 3
- •Билет № 5
- •Билет № 6
- •Билет № 7
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 8
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 9
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 10
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 11
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 12
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 13
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 14
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 15
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 16
- •3. Задачи 3, 4, 5 из приложения к билету.
- •2)Основные правила нахождения производной
- •Билет № 17
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 18
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 19
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 20
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 21
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 22
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 23
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 24
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 25
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Системы координат на плоскости и в пространстве
- •Свойства компланарности
- •Условия коллинеарности векторов
- •Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
- •[Править]Вырожденные кривые
- •Односторонний предел по Коши
- •Дифференцируемость функции и дифференциал
- •Точка перегиба функции
- •Неофициальное
- •Условия существования
Односторонний предел по Коши
Число
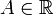 называется правосторонним
пределом (правым
пределом, пределом
справа)
функции
называется правосторонним
пределом (правым
пределом, пределом
справа)
функции 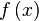 в
точке
в
точке 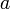 ,
если для всякого положительного
числа
,
если для всякого положительного
числа  отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число 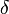 такое,
что для всех
точек
такое,
что для всех
точек 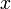 из интервала
из интервала 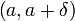 справедливо неравенство
справедливо неравенство 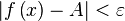 .
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число , такое, что для всех точек из интервала
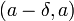 справедливо
неравенство
.[1]
справедливо
неравенство
.[1]
![]()
Дифференцируемость функции и дифференциал
Пусть
функция ![]() задана
в некоторой области
задана
в некоторой области ![]() ,
и
,
и ![]() --
внутренняя точка этой области. Пусть
--
внутренняя точка этой области. Пусть ![]() --
произвольная точка этой же области
--
произвольная точка этой же области ![]() .
Разность
.
Разность ![]() называется приращением
аргумента
;
называется приращением
аргумента
; ![]() ,
где
,
где ![]() .
Разность значений функции
.
Разность значений функции ![]() называется приращением,
или полным
приращением функции
называется приращением,
или полным
приращением функции ![]() в
точке
,
соответствующим приращению
аргумента
в
точке
,
соответствующим приращению
аргумента ![]() ;
; ![]() --
это функция от точки
и
приращения
.
--
это функция от точки
и
приращения
.
Предположим, что приращение функции можно представить в виде
|
(7.2) |
где ![]() --
некоторые числа. Подчеркнём, что эти
числа не зависят от
,
но могут измениться, если сменить
точку
.
Относительно величины
--
некоторые числа. Подчеркнём, что эти
числа не зависят от
,
но могут измениться, если сменить
точку
.
Относительно величины ![]() мы
предположим, что это функция, при
базе
мы
предположим, что это функция, при
базе ![]() являющаяся
величиной большего порядка малости,
чем
являющаяся
величиной большего порядка малости,
чем ![]() .
Это означает, если вспомнить определение
бесконечно малой величины большего
порядка малости относительно другой
бесконечно малой, что
.
Это означает, если вспомнить определение
бесконечно малой величины большего
порядка малости относительно другой
бесконечно малой, что
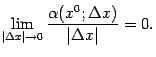
Заметим, что сумма всех слагаемых левой части (7.2), кроме последнего, -- это линейная функция от приращения аргумента , если точка фиксирована. Условие большей малости последнего слагаемого (7.2) относительно означает, что эта линейная функция -- главная часть приращения функции.
Определение 7.11 Если указанное представление (7.2) имеет место, то функцию называют дифференцируемой в точке , а линейную относительно функцию
![]()
то есть главную линейную часть приращения функции, -- дифференциалом функции в точке .
Если функция является дифференцируемой в любой точке открытой области , то функцию называют дифференцируемой в области .
Таким
образом, приращение ![]() дифференцируемой
функции можно представить в виде суммы
дифференциала
дифференцируемой
функции можно представить в виде суммы
дифференциала ![]() ,
то есть линейной части приращения, и
остатка
,
то есть линейной части приращения, и
остатка ![]() ,
который имеет более высокий порядок
малости, чем приращение
:
,
который имеет более высокий порядок
малости, чем приращение
:
![]()
Теорема 7.8 Дифференцируемая в точке функция является непрерывной в этой точке.
Доказательство.
Действительно, если ![]() ,
то стремятся к 0 все слагаемые дифференциала:
они имеют вид
,
то стремятся к 0 все слагаемые дифференциала:
они имеют вид ![]() ;
множитель
;
множитель ![]() не
зависит от
,
то есть постоянен, а
не
зависит от
,
то есть постоянен, а![]() ,
поскольку
,
поскольку ![]() Величина
также
стремится к 0, так как имеет даже больший
порядок малости, чем
.
Значит,
Величина
также
стремится к 0, так как имеет даже больший
порядок малости, чем
.
Значит, ![]() .
Но условие
.
Но условие ![]() как
раз и означает, что
как
раз и означает, что ![]() при
при ![]() ,
то есть что функция
непрерывна
в точке
.
,
то есть что функция
непрерывна
в точке
.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
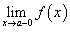 и
правосторонний предел
и
правосторонний предел 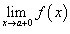 ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов![]() называется скачком
функции.
называется скачком
функции.
Дифференциалы высших порядков
Пусть в интервале (a, b) задана дважды дифференцируемая функция y = f(x), где x — независимая переменная.
Фиксируем приращение dx = Δx независимой переменной x, т.е. будем считать первый дифференциал
|
dy = f'(x) dx |
(1) |
функцией только переменной x.
Дифференциал от первого дифференциала, при условии, что повторное приращение независимой переменной x совпадает с первоначальным, называется вторым дифференциалом функции f(x) в точке x и обозначается d2 f(x).
Дифференцируем выражение в правой части (1) как произведение
|
d2 f(x) = d (df(x) ) = d (f'(x) dx) = f''(x) dx · dx + f'(x) · d(dx) . |
