Условия коллинеарности векторов

• Два вектора коллинеарные, если отношения их координат равны.

• Два вектора коллинеарные, если их векторное произведение равно нулю.

• Так в случае плоской задачи вектора 

•  коллинеарны если

ax	=	ay	.
bx		by
Так в случае пространственной задачи вектора коллинеарны если ax  =  ay  =  az . bx by bz

Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника

1. Если x₁ и y₁ - координаты точки A, а x₂ и y₂ - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении  , определяются по формулам

Если  , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

2. Площадь треугольника по известным координатам его вершин A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) вычисляется по формуле

Полученное с помощью этой формулы число следует взять по абсолютной величине.

3. Площадь многоугольника с вершинами A(x₁, y₁), B(x₂, y₂), C(x₃, y₃), ..., F(x_n, y_n) равна

Выражение вида   равно x₁y₂ - x₂y₁ и называется определителем второго порядка.

Уравнения прямой на плоскости

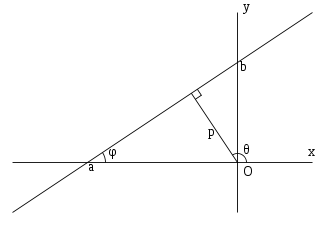
Способы задания прямой:  или  .

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где  ,   и   — произвольные постоянные, причем постоянные   и   не равны нулю одновременно. Вектор с координатами  называется нормальным вектором, он перпендикулярен прямой.

При   прямая проходит через начало координат. Также уравнение можно переписать в виде

Классификация кривых второго порядка

[править]Невырожденные кривые

Кривая второго порядка называется невырожденной, если   Могут возникать следующие варианты:

• Невырожденная кривая второго порядка называется центральной, если 

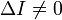
  • эллипс — при услови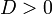и   и  ;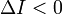

    • частный случай эллипса — окружность — при услови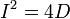и   или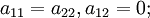 

  • мнимый эллипс (ни одной вещественной точки) — при условии 

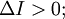
  • гипербола — при условии 

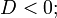
• Невырожденная кривая второго порядка называется нецентральной, если 

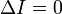
  • парабола — при условии 

[Править]Вырожденные кривые

Кривая второго порядка называется вырожденной, если  . Могут возникать следующие варианты:

• вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии 

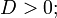
• пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии 

• вырожденная парабола — при условии 

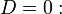
  • пара вещественных параллельных прямых — при условии 

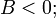
  • одна вещественная прямая (две слившиеся параллельные прямые) — при условии 

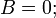
  • пара мнимых параллельных прямых (ни одной вещественной точки) — при условии 

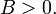
Неполные уравнения прямой на плоскости.

Определение. Уравнение

                                                                      (2)

 называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю.

   Если коэффициент  ,  , то из уравнения (2) следует  . Это уравнение прямой, параллельной оси Оу, отсекающей от оси Ох отрезок величиной а.

Если коэффициент  ,   то из уравнения (2) следует  . Это уравнение прямой, параллельной оси Ох, отсекающей от оси Оу отрезок величиной b.

               

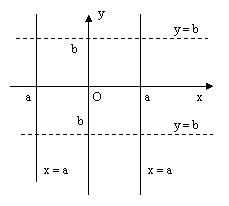
                                       рис.5.

Если  , то уравнение (2) принимает вид

                                 .                                          (9)

Ясно, что эта прямая проходит через начало координат.

   Если в уравнении (9) коэффициент  , то отсюда получаем  . Обозначив через  , получаем уравнение, которое носит название уравнения прямой с угловым коэффициентом   , которое изучалось в школьном курсе алгебры.

   Если в уравнении (9)  , то   и, сокращая на А, получаемуравнение оси Оу:   .

   Если в уравнении (9)  , то   и, сокращая на В, получаемуравнение оси Ох:  .

   Подведем итог исследования общего уравнения прямой

                                                                      (2)

1) Если  , то уравнение (2) может быть записано в виде уравнения прямой в отрезках:

                                            

– прямая, отсекающая от осей координат отрезки величиной а и b соответственно.

2) Если  , то уравнение может быть записано в виде:

                                            

– прямая параллельная оси Ох и отсекающая от оси Оу отрезок величины b.

3) Если  , то уравнение может быть записано в виде:

                                            

– прямая параллельная оси Оу и отсекающая от оси Ох отрезок величины а.

4) Если  , то уравнение прямой имеет вид

                                            

– прямая совпадает с осью Ох.

5) Если  , то уравнение прямой имеет вид

                                            

– прямая совпадает с осью Оу.

6) Если  , то уравнение может быть записано в виде:   – уравнение прямой с угловым коэффициентом.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).