
- •Билет № 1
- •Билет № 2
- •Билет № 3
- •Билет № 5
- •Билет № 6
- •Билет № 7
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 8
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 9
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 10
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 11
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 12
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 13
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 14
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 15
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 16
- •3. Задачи 3, 4, 5 из приложения к билету.
- •2)Основные правила нахождения производной
- •Билет № 17
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 18
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 19
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 20
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 21
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 22
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 23
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 24
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Билет № 25
- •3. Задачи 3, 4, 5 из приложения к билету.
- •Системы координат на плоскости и в пространстве
- •Свойства компланарности
- •Условия коллинеарности векторов
- •Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
- •[Править]Вырожденные кривые
- •Односторонний предел по Коши
- •Дифференцируемость функции и дифференциал
- •Точка перегиба функции
- •Неофициальное
- •Условия существования
Билет № 23
1. Системы линейных алгебраических уравнений.
2. Взаимное расположение прямых в пространстве.
3. Задачи 3, 4, 5 из приложения к билету.
1) Система
![]() линейных
алгебраических уравнений
с
линейных
алгебраических уравнений
с
![]() неизвестными —
это система уравнений вида
неизвестными —
это система уравнений вида
![]() Матрица коэффициентов системы; столбец
неизвестных Х(х1 х2 хn);
В(b1
b2
bn)
столбец свободных членов
Матрица коэффициентов системы; столбец
неизвестных Х(х1 х2 хn);
В(b1
b2
bn)
столбец свободных членов
2) Взаимное расположение прямых
y=k1x+b1 y= k2x+b2
k1=k2-параллельны, k1k2=-1-перпендикулярны
![]()
![]()
![]() ={А1,
В1}
={А1,
В1}
![]() ={А2,
В2}
={А2,
В2}
![]() -параллельны
прямые (прямые не совпадают и не
пересекаются)
-параллельны
прямые (прямые не совпадают и не
пересекаются)
Необходимым и достаточным условием перпендикулярности прямых
![]()
Билет № 24
1. Матричный метод решения систем линейных алгебраических уравнений.
2. Касательная и нормаль к плоской кривой.
3. Задачи 3, 4, 5 из приложения к билету.
1) Пусть дана система линейных уравнений
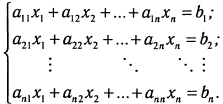
Если ввести матричные обозначения
![]()
то систему можно
записать матричным уравнением
![]() Решение системы матричным методом
определяется соотношением
Решение системы матричным методом
определяется соотношением
![]()
2)Из
геометрического смысла производной
следует, что угловой коэффициент
касательной к кривой
![]() в точке
в точке
![]() равен значению производной в этой точке,
т. е.
равен значению производной в этой точке,
т. е.
![]() касательной к кривой в точке имеет вид
касательной к кривой в точке имеет вид
![]()
Нормалью к
кривой в точке
![]() называется прямая, проходящая через
точку М
перпендикулярно
касательной к кривой в этой точке. В
силу условия перпендикулярности двух
прямых
называется прямая, проходящая через
точку М
перпендикулярно
касательной к кривой в этой точке. В
силу условия перпендикулярности двух
прямых![]() уравнение нормали имеет вид
уравнение нормали имеет вид
![]()
Билет № 25
1. Метод Крамера решения систем линейных алгебраических уравнений.
2. Вычисление площадей при помощи определённого интеграла.
3. Задачи 3, 4, 5 из приложения к билету.
1) Решение системы двух линейных уравнений с двумя неизвестными
![]() по формулам Крамера
имеет вид
по формулам Крамера
имеет вид![]()
Где
![]() основной и дополнительные определители
системы.
основной и дополнительные определители
системы.
![]() — система совместна,
имеет единственное решение;
— система совместна,
имеет единственное решение;
![]() — система несовместна,
не имеет решения;
— система несовместна,
не имеет решения;
![]() — система
неопределенна, т. е. имеет бесчисленное
множество решений (система сводится к
одному уравнению).
— система
неопределенна, т. е. имеет бесчисленное
множество решений (система сводится к
одному уравнению).
Однородная система трех линейных уравнений с тремя неизвестными
![]()
![]() система имеет
единственное решение, определяемое по
формулам Крамера решению
система имеет
единственное решение, определяемое по
формулам Крамера решению
![]()
Системы координат на плоскости и в пространстве
Системы координат на плоскости Декартовы прямоугольные координаты (рис. 4.1)
О -
начало координат, Ох -
ось абсцисс, Оy -
ось ординат, ![]() -
базисные векторы,
-
базисные векторы, ![]() -
абсцисса точки M (
-
абсцисса точки M (![]() -
проекция точки M на
ось Ох параллельно
оси Оy),
-
проекция точки M на
ось Ох параллельно
оси Оy), ![]() -
ордината точки M (
-
ордината точки M (![]() -
проекция точки M на
ось Oy параллельно
оси Ox).
-
проекция точки M на
ось Oy параллельно
оси Ox).

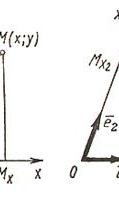
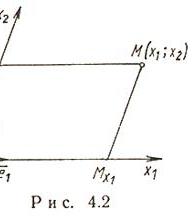
Декартовы косоугольные (афинные) координаты (рис. 4.2)
О -
начало координат, ![]() -
оси координат,
-
оси координат, ![]() ,
, ![]() -
координаты точки M (
-
координаты точки M (![]() -
проекция точки M на
ось
-
проекция точки M на
ось ![]() параллельно
оси
параллельно
оси ![]() ,
аналогично
,
аналогично ![]() ),
), ![]() -
базисные векторы.
-
базисные векторы.
Полярные координаты (
О -
полюс, Ox -
полярная ось, ![]() -
полярный радиус,
-
полярный радиус, ![]() -
полярный угол.
-
полярный угол.
Главные
значения ![]() и
:
и
: ![]() (иногда
(иногда ![]() ).
).
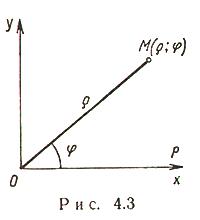
Выражение декартовых прямоугольных координат через полярные
![]()
![]() Выражение
полярных координат через декартовы
прямоугольные
Выражение
полярных координат через декартовы
прямоугольные
![]()
Условия коллинеарности и компланарности векторов.
Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости
Свойства компланарности
Пусть ![]() —
векторы пространства
—
векторы пространства ![]() .
Тогда верны следующие утверждения:
.
Тогда верны следующие утверждения:
Если хотя бы один из трёх векторов — нулевой, то три вектора тоже считаются компланарными.
Тройка векторов, содержащая пару коллинеарных векторов, компланарна.
Смешанное произведение компланарных векторов
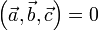 .
Это — критерий компланарности трёх
векторов.
.
Это — критерий компланарности трёх
векторов.Компланарные векторы — линейно зависимы. Это — тоже критерий компланарности.
Существуют действительные числа
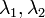 такие,
что
такие,
что 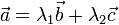 для
компланарных
для
компланарных 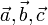 ,
за исключением случаев
,
за исключением случаев 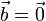 или
или 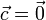 .
Это — переформулировка предыдущего
свойства и тоже критерий компланарности.
.
Это — переформулировка предыдущего
свойства и тоже критерий компланарности.В 3-мерном пространстве 3 некомпланарных вектора образуют базис. То есть любой вектор
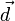 можно
представить в виде:
можно
представить в виде: 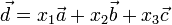 .
Тогда
.
Тогда 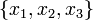 будут
координатами
в
данном базисе.
будут
координатами
в
данном базисе.
