Билет № 20

1. Векторы. Линейные действия над векторами.

2. Непрерывность функции в точке. Точки разрыва.

3. Задачи 3, 4, 5 из приложения к билету.

1) Вектором называется направленный отрезок с началом в точке A и концом в точке B.

Суммой векторов и называется вектор который получается при совмещении конца вектора с началом вектора . Тогда началом вектора будет начало вектора , а концом вектора - конец вектора .

Сумма векторов обладает свойствами сочетательности и переместительности

Вектор называется разностью векторов если сумма векторов равна вектору т. е. если

2) Функция непрерывна в точке х = а, если пределы слева и справа равны и равны значению функции в этой точке, т. е.

Функция непрерывна в точке х = а, если она определена в этой точке и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, вблизи точки а.

Сумма, разность и произведение конечного числа непрерывных функций есть функция непрерывная.

Непрерывная на отрезке функция принимает любое промежуточное значение между ее наименьшим т и наибольшим М значением, то есть

Значения аргумента, которые не удовлетворяют условиям непрерывности, называются точками разрыва функции. При этом различают два рода точек разрыва функции.

Если при слева функция имеет конечный предел а при справа функция имеет конечный предел то говорят, что функция при имеет разрыв первого рода.

Если значение функции при равно то говорят, что функция непрерывна слева; если же то говорят, что функция непрерывна справа.

Если говорят, что функция имеет в точке а устранимый разрыв.

Если при справа или слева, предел функции не существует или равен бесконечности, то есть то говорят, что при функция имеет разрыв второго рода.

Билет № 21

1. Миноры и алгебраические дополнения. Теорема разложения.

2. Бесконечно малые и бесконечно большие функции, связь между ними.

3. Задачи 3, 4, 5 из приложения к билету.

1) Минором некоторого элемента определителя называется определитель, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых этот элемент находится. Так для элемента минор обозначается

Алгебраическим дополнением некоторого элемента определителя называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, на пересечении которых находится этот элемент—число четное и со знаком минус, если эта сумма — число нечетное. Алгебраическое дополнение элемента будет

2)Ф-ция назыв бесконечно малой при x0, если lim x0 =0

Ф-ция называется бесконечно большой при x0, если lim x0 =

(1/0)= обратная к бесконечно малой при x0, бесконечно большая и наоборот (1/ )=0

Билет № 22

1. Обратная матрица и её вычисление.

2. Понятие функции. Классы функций. Сложная функция.

3. Задачи 3, 4, 5 из приложения к билету.

1) Обратной матрицей по отношению к заданной квадратной матрице А называется такая квадратная матрица, обозначаемая которая удовлетворяет равенствам

Нахождение обратной матрицы :

1. находим определитель |А| = 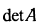Если он не равен нулю, то

2. находим алгебраические дополнения 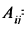всех элементов матрицы А

3. составляем из них матрицу А*

4. транспорируем ее (А*)^Т

5. получаем обратную матрицу

2)Переменную х называют независимой переменной или аргументом, а у — функцией. Функция может задаваться аналитически, графически и таблично.

К основным элементарным функциям относятся пять классов функций: степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические.

Пусть каждому значению переменной х ставится в соответствие определенное значение переменной а каждому уже определенному значению и ставится в соответствие определенное значение тогда соответствие между значениями имеет вид и определяет у как сложную функцию от х, т. е. функцию от функции.