3. Задачи 3, 4, 5 из приложения к билету.

1)Векторное произведение векторов назыв вектор, обозначаемой ([ ],[ ]) и удовлетворяющий трем св-вам:

1. длина векторного произведения равна-

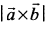
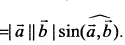
2. вектор перпендикулярен векторам

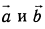
3. вектор направлен в ту сторону с которой поворот от 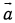к 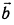видится против часовой стрелки.

Св-ва геометрические

1. длина векторного произведения численно равна площади параллелограмма, построенного на векторах

2. векторы коллинеарны тогда и только тогда, когда * =0. В частности * =0

Алгебраические:

2. Замечательные пределы 1. Первый замечательный предел

2. Второй замечательный предел

Билет № 16

1. Скалярное произведение векторов, его свойства.

2. Основные правила нахождения производных. Примеры.

3. Задачи 3, 4, 5 из приложения к билету.

1) Скалярным произведением двух векторов называется скаляр (число), равное произведению модулей перемножамых векторов на косинус угла между ними

Свойства

1. Переместительность

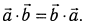
2. Распределительность

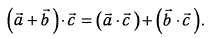
3.Скалярный множитель можно выносить за знак скалярного произведения

4. Скалярный квадрат вектора равен квадрату его модуля

5. Скалярное произведение единичных векторов определяется формулами

2)Основные правила нахождения производной

Билет № 17

1. Проекция вектора на ось.

2. Наибольшее и наименьшее значения функции на отрезке.

3. Задачи 3, 4, 5 из приложения к билету.

1) Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора

2)Наибольшим значением функции а некотором отрезке называется самое большое, а наименьшим значением — самое меньшее из всех ее значений.

Если функция непрерывна в некотором интервале и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале (конечном или бесконечном).

Билет № 18

1. Базис и координаты вектора в пространстве.

2. Производная функции, заданной параметрически.

3. Задачи 3, 4, 5 из приложения к билету.

1) Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке. Эти векторы называются базисными.

Коэффициенты в разложении называются координатами вектора относительно базиса (число , называют абсциссой, — ординатой, а — аппликатой вектора).

2)Если функциональная зависимость между переменными задана параметрически. TO производная от равна

Билет № 19

1. Базис и координаты вектора на плоскости.

2. Сравнение и эквивалентность бесконечно малых.

3. Задачи 3, 4, 5 из приложения к билету.

1) Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определённом порядке. Эти векторы называются базисными.

Коэффициенты и в разложении (1.3) называются координатами вектора а относительно базиса (число называют абсциссой, а — ординатой вектора ).

2) Ф-ция назыв бесконечно малой при x0, если lim x0 =0 Отношение бесконечно малых величин образует так называемую неопределённость .

Если , то β — бесконечно малая высшего порядка малости, чем α.

Если , то β — бесконечно малая низшего порядка малости, чем α.

Если (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.

Если , то бесконечно малые величины α и β называются эквивалентными ( ).

При справедливы следующие соотношения эквивалентности







