Экзаменационный билет(Городниченко)
Кафедра «Технологии и системы связи»
Дисциплина «Технологии цифровой связи»
Специальность 5В071900 «Теория электрической связи»
Спектры сигналов
Спектр сигнала - это совокупность гармонических составляющих с конкретными значениями частот, амплитуд и начальных фаз, образующих в сумме сигнал. Практически пользуются амплитудной спектральной диаграммой.
Шириной
спектра сигнала
называется минимальная полоса частот,
на которой сосредоточена подавляющая
часть (95%) мощности (или энергии) сигнала.
Для спектрального представления
непериодических (импульсных) сигналов,
заданных на конечном интервале
,
непосредственно воспользоваться рядом
Фурье нельзя, так как импульсный сигнал
не является периодическим. Для
гармонического разложения сигнала
выполняется следующее:
импульсный сигнал u (t) дополняется до периодического с любым периодом Т, включающим в себя промежуток ;
полученный периодический сигнал u пер(t) представляется в виде ряда Фурье;
затем производится предельный переход от u пер(t) к u (t) при
.
Для вычисления спектра в этом случае пользуются комплексной формой записи ряда Фурье:
(обратное
преобразование Фурье), где
(прямое
преобразование Фурье).
Комплексная спектральная плотность:
где
модуль
или спектральная
плотность амплитуд (амплитудный
спектр);
аргумент
или фазовый
спектр
непериодического сигнала.
Поскольку сигналы и помехи - это случайные процессы, то знание спектра помехи позволяет предпринимать меры для ее подавления. Таким образом, спектр необходимо знать для осуществления неискаженной передачи сигнала по каналу связи, для обеспечения разделения сигналов и ослабления помех.Ширина спектра - это интервал частот, занимаемый спектром сигнала. Ширина спектра импульсных сигналов обратно пропорциональна длительности импульса.
Понятие «детерминированная» функция, «финитный» процесс
Сообщения,
сигналы, помехи являются случайными
процессами и для их исследования
используются основные положения теории
случайных процессов. Неслучайная функция
времени называется детерминированной.
Случайный процесс может быть задан на
дискретном множестве значений t.
Процессы, заданные на конечном отрезке
времени, называются финитными.
Случайные
процессы бывают различных типов.
Различают дискретные и непрерывные
процессы. Для дискретного
процесса
случайная
величина Х может принимать только
конечное множество значений
для непрерывного
- любые
значения х из некоторого интервала,
даже бесконечного. Для математического
описания случайных величин вводятся
следующие неслучайные основные
статистические характеристики:
Функция распределения вероятности:
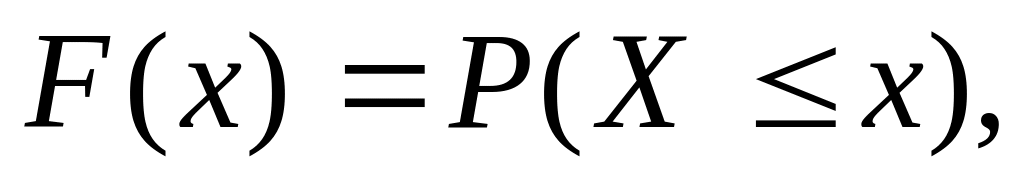показывающая
вероятность того, что значения случайной
величиныне превысят конкретно выбранного
значения х. Если случайная величина Х
принимает дискретные значения, то F(x)
- дискретная функция. Если Х - непрерывная
случайная величина, то F(х)
- монотонно возрастающая функция,
значение которой лежат в интервале
,
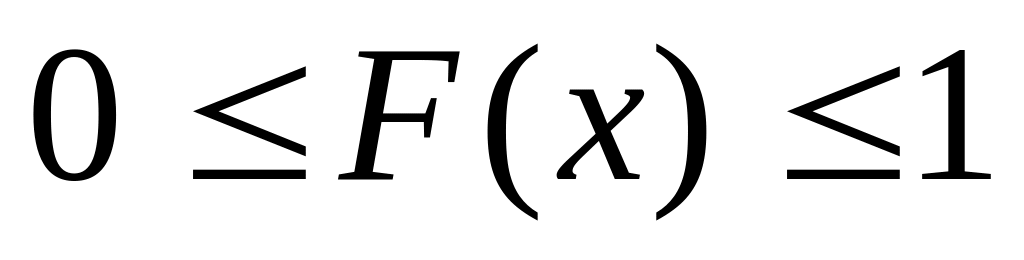причем
Плотность распределения вероятности, которая вычисляется как производная от функции распределения:
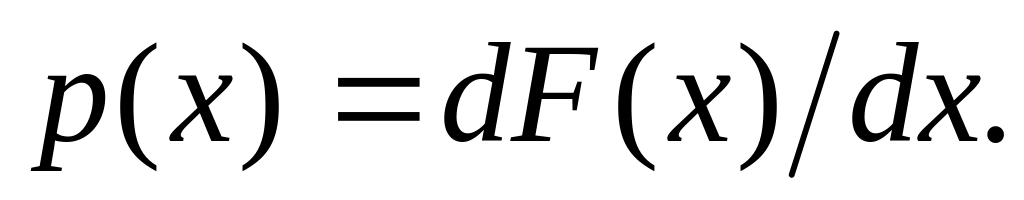Физически p(x)
- это вероятность попадания случайной
величины в малый интервал dx
в окрестности точки х.Математическое ожидание - это среднее значение процесса по ансамблю:
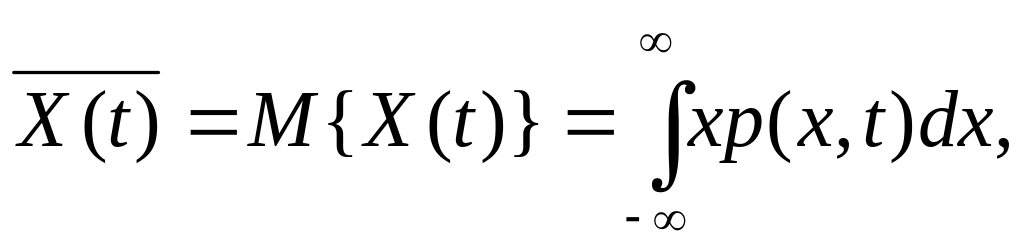где p(x,t)
- одномерная плотность распределения
для сечения t.
Разность между случайным процессом и
его математическим ожиданием называется
центрированным процессом, обозначается
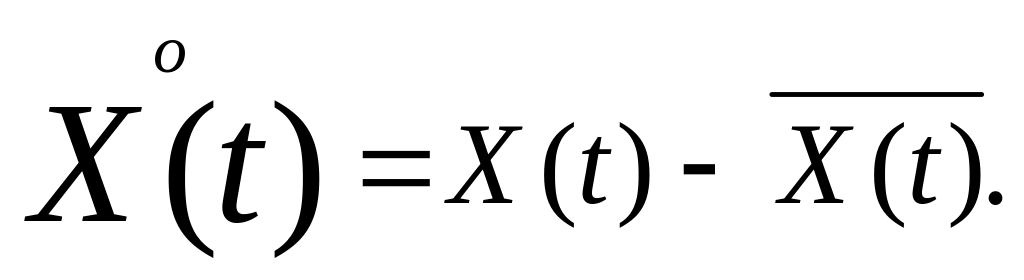
Математическое ожидание квадрата центрированного процесса называется дисперсией:
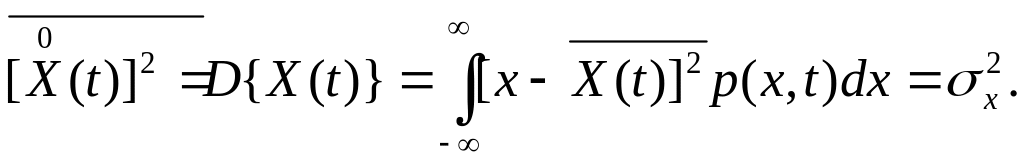
Дисперсия
количественно характеризует степень
разброса результатов относительно
среднего значения. По физическому смыслу
- это среднеквадратичное отклонение
(эффективное значение).
Задача
Дать общую характеристику и классификацию корректирующих кодов.
Изложить принцип построения кодов, обнаруживающих и исправляющих ошибки.
Изложить функциональную схему кодирующего устройства кода Хэмминга
Построить код Хэмминга, взяв в качестве исходной кодовой комбинации двоичное число, полученное из двух последних цифр шифра студента. Определить вероятность ошибочного приема полученной кодовой комбинации кода Хэмминга и вероятность появления необкарироваемой ошибки .
Зав кафедрой
Протокол №17
от 02.05.2012 г
Министерство образования и науки Республики Казахстан
Карагандинский Государственный Технический Университет