2. Виды относительных величин

1. Относ. величина выполнения плана: i_{вып. пл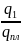} = = 1,02(выполнен на 2) или 102%(перевыполнено на 102%)

2. Относ. величина планового задания: i _{пл. зад} = =108%планом предусмотрено по сравнению с прошлым годом на 8%

3. Относ. величина динамики: i_дин =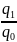 =115,2% (увел на 15,2) или 98% (уменьшение на 2)

i_дин = i_{вып. пл} ∙ i _{пл. зад}

Планом было предусмотрено 12,5% фактический показатель увеличился на 14,8%. Как был выполнен план?

i_{вып. пл}= =1,02 (план перевыполнен на 2%)

4. Относительная величина структуры – показывает дела каждой группы в общей совокупности.

Рабочие 140чел

Специалисты и служащие 82чел

Вспомогательный персонал 15чел

Итого: 237чел

iстр = ∙ 100%= 59,1% - увеличенный вес рабочих в общей численности

iстр = ∙ 100%= 34,6%

iстр = ∙ 100%= 6,3%

Наибольший удельный вес занимают рабочие.

5. Относительная величина координации – получают сравнение одной величины с другой, за базу сравнения берется большая величина.

Определением сколько специалистов приходится на 100 рабочих?

∙ 100 раб= 58 чел

∙ 100 раб= 10 чел

6. Относительная величина интенсивности – показывает распространение изучаемого явления в опр. среде.

Телефонная плотность: ∙ 100 чел N- кол-во телефон(посылок)

Душевой уровень потребления услуг связи: ∙ 100 чел Н- численность населения

7. Относительная величина сравнения – показывает отношение одной абсолютной величины и другой относящихся к разным объектам или территориям.

А – 1200 чел	iср = = 3,5 раза
В – 345 чел

Средние величины

1. Понятие средней величины и виды средней

Средние величины – стат показатель, дающий обобщающую характеристику изучаемого признака.

З = =

Средняя стат величина отличается от средней математической величины. Средняя мат величина-отвлеченная, средняя стат величина характеризует конкретные явления.

В средней величине проявляется закон больших чисел – погашает все случайные отклонения у отдельных признаков.

Виды средних: ср арифметическая простая и взвешенная; ср гармоническая; ср прогрессивная; ср хронологическая; ср геометрическая; ср квадратическая.

2. Средняя арифметическая простая и взвешенная

Пример: Определить средний возраст рабочих цеха по следующим данным:

возраст (лет) – 15; 25; 30; 42; 30; 45; 18; 25; 30; 25; 42

сред возраст = = 29,5 лет

Обозначим через Х индивидуальные значения возраста. Обозначим через n кол-во единиц которое обладает данным признаком и запишем формулу:

= = – средняя арифметическая простая

Сгруппируем всех рабочих бригады по возрасту и представим в виде ряда распределения

Возраст лет (Х)	Кол-во работников(m)	xm
18	2	36
25	4	100
30	3	90
42	2	24
45	1	45
Итого	12	355

Ряд распределения состоит из 2 составляющих:

• Индивидуальное значение признака или варианта (Х)

• Кол-во работников (m) – частота, сколько раз повториться индивидуальный распределенный признак в ряду распределения

= = – средняя арифметическая взвешенная

Если ряд распределения интервальный, то в этом случае сначала находят середину каждого интервала это и будет Х , а затем находят среднею арифметическую взвешенную.