621.3(075)
С 232
М
ИНОБРНАУКИ
РОССИИ
Федеральное государственное автономное образовательное
учреждение высшего профессионального образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
КАФЕДРА МЕХАТРОНИКИ И ЭЛЕКТРОТЕХНИКИ
Д.П. Рассоха
Сборник индивидуальных
домашних заданий с примерами выполнения
по курсу
Теоретические основы
Электротехники
Для студентов дневной формы обучения всех специальностей
Таганрог 2012
УДК 621.3.011.1(07.07)
Д.П. Рассоха. Сборник индивидуальных домашних заданий с примерами выполнения по курсу «Теоретические основы электротехники».
Для студентов дневной формы обучения все специальностей. - Таганрог: Изд-во ТТИ ЮФУ, 2012. - 72 с.
Методические материалы, изложенные в данной работе, содержат всю необходимую информацию по выполнению индивидуального задания по курсу «Теоретические основы электротехники». Выполнение индивидуального задания ориентировано на оптимальное сочетание индивидуальной самостоятельной работы студентов и аудиторных занятий.
Цель данной работы заключается в оказании методической помощи студентам, изучающим курс «Теоретические основы электротехники».
Табл. 14. Библиогр.: 17 назв.
Рецензент А.А. Шеслер, канд. техн. наук, директор НПТК “АВС-LTD”.
ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ В г. ТАГАНРОГЕ 2012г.
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ 3
Индивидуальное домашние задание № 1 Расчет цепи с диодами на постоянном токе в установившемся режиме 4
Индивидуальное задание № 2. Анализ переходных процессов в линейных цепях 17
Задача № 1. Расчет переходных процессов в линейных цепях с синусоидальными источниками электрической энергии классическим методом 17
Прядок расчета переходного процесса классическим методом: 20
1. Пример выполнения расчета переходного процесса в цепи второго порядка классическим методом 22
Задача № 2. Анализ переходных процессов в линейных цепях операторным методом 32
. Задача № 3. Расчет переходного процесса с источником произвольной формы интегралом Дюамеля 40
Задача № 5. Анализ переходных процессов в линейных цепях методом переменных состояния 60
Библиографический список 68
Предисловие
Учебное пособие предназначено для студентов всех специальностей, изучающих теорию электрических цепей.
Сборник индивидуальных домашних заданий включает следующие разделы:
- расчет цепи с диодами на постоянном токе в установившемся режиме;
- расчет переходных процессов в линейных цепях классическим методом;
- расчет переходных процессов в линейных цепях операторным методом;
- расчет переходного процесса с источником произвольной формы интегралом Дюамеля.
Каждая тема в сборнике включает сто вариантов типовых задач с подробным решением нулевого варианта. Варианты определяются по последним двум цифрам зачетной книжки или студенческого билета. Например, номер зачетной книжки – 025221, вариант равен 21.
Индивидуальное домашние задание № 1 Расчет цепи с диодами на постоянном токе в установившемся режиме
Д
ля
получения расчетной схемы, необходимо
в топологию цепи (рис. 1) поместить
элементы из таблицы 1, которые указаны
буквами. Если в таблице 1 элементы
записаны через запятую, то они включаются
в ветвь последовательно. Направление
источников и диодов должно совпадать
с направление указанным в ветвях
топологической схемы. Если перед
источниками стоит знак минус, то его
значение берется со знаком минус, или
меняется направление источника.
Вариант задается преподавателем или определяется по последним двум цифрам зачетной книжки (студенческого билета).
Назначение букв в таблице следующее: |
|
Численное значение элементов для всех вариантов равно: |
Е - постоянный источника ЭДС |
|
Е = 20 B |
J - постоянный источника тока |
|
J = 2 A |
R - сопротивление |
|
R = 10 Ом |
D - диод |
|
|
Для расчетной схемы, согласно заданному варианту, необходимо решить следующие задачи:
Задача №1. Для заданного диода снять вольтамперную характеристику (ВАХ) в программе Multisim.
Задача №2. Выполнить моделирования заданной цепи в программе Multisim
Задача №3. Рассчитать режим работы нелинейной цепи, используя метод простой итерации, если вольтамперная характеристика диода задана виде графика снятой в программе Multisim;
Задача
№4. Выполнить аппроксимацию
ВАХ диода используя выражение
и рассчитать заданную цепь используя
процедуру Given
…… Minerr
программы Mathcad.
Задача №5Рассчитать токи и напряжения во всех ветвях, используя матричный метод расчета сложных цепей. Правильность расчёта проверить через уравнения баланса мощностей. Значение сопротивления Rст диодов взять из задач 1, 2или 3.
Таблица 1.
Вариант |
Диод |
Номер ветви |
|||||||||
№ |
Тип диода |
Знач N |
Ток Is, мА |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1N4001 |
5 |
100 |
R |
D |
D |
R |
E,R |
J |
R |
J |
|
|
1N4001GP |
6 |
150 |
J |
R |
D |
D |
R |
E,R |
J |
R |
|
|
1N4002 |
7 |
200 |
R |
J |
R |
D |
D |
R |
E,R |
J |
|
|
1N4002GP |
8 |
250 |
J |
R |
J |
R |
D |
D |
R |
E,R |
|
|
1N4003 |
9 |
100 |
E,R |
J |
R |
J |
R |
D |
D |
R |
|
|
1N4003GP |
10 |
150 |
R |
E,R |
J |
R |
J |
R |
D |
D |
|
|
1N4004 |
11 |
200 |
D |
R |
E,R |
J |
R |
J |
R |
D |
|
|
1N4004GP |
12 |
250 |
D |
D |
R |
E,R |
J |
R |
J |
R |
|
|
1N4005 |
5 |
100 |
J |
D |
E,R |
D |
R |
R |
J |
R |
|
|
1N4005GP |
6 |
150 |
R |
J |
D |
E,R |
D |
R |
R |
J |
|
|
1N4006 |
7 |
200 |
J |
R |
J |
D |
E,R |
D |
R |
R |
|
|
1N4006GP |
8 |
250 |
R |
J |
R |
J |
D |
E,R |
D |
R |
|
|
1N4007 |
9 |
100 |
R |
R |
J |
R |
J |
D |
E,R |
D |
|
|
1N4007GP |
10 |
150 |
D |
R |
R |
J |
R |
J |
D |
E,R |
|
|
1N4148 |
11 |
200 |
-E,R |
D |
R |
R |
J |
R |
J |
D |
|
|
1N4245GP |
12 |
250 |
D |
E,R |
D |
R |
R |
J |
R |
J |
|
|
1N4246GP |
5 |
100 |
D |
R |
E,R |
R |
J |
J |
D |
R |
|
|
1N4247GP |
6 |
150 |
R |
D |
R |
E,R |
R |
J |
J |
D |
|
|
1N4248GP |
7 |
200 |
D |
R |
D |
R |
E,R |
R |
J |
J |
|
|
1N4249GP |
8 |
250 |
-J |
D |
R |
D |
R |
E,R |
R |
J |
|
|
1N4383GP |
9 |
100 |
-J |
J |
D |
R |
D |
R |
E,R |
R |
|
|
1N4384GP |
10 |
150 |
R |
J |
J |
D |
R |
D |
R |
E,R |
|
|
1N4385GP |
11 |
200 |
-E,R |
R |
J |
J |
D |
R |
D |
R |
|
|
1N4531 |
12 |
250 |
R |
E,R |
R |
J |
J |
D |
R |
D |
|
|
1N4532 |
5 |
100 |
R |
D |
J |
D |
R |
E,R |
R |
J |
|
|
1N4534 |
6 |
150 |
-J |
R |
E,R |
D |
D |
R |
J |
R |
|
|
1N4585GP |
7 |
200 |
R |
J |
R |
R |
D |
D |
E,R |
J |
|
|
1N4585GP |
8 |
250 |
-J |
R |
D |
J |
R |
D |
R |
E,R |
|
|
1N4586GP |
9 |
100 |
-E,R |
J |
D |
R |
J |
R |
D |
R |
|
|
1N4933 |
10 |
150 |
R |
E,R |
R |
J |
R |
J |
D |
D |
|
|
1N4933GP |
11 |
200 |
D |
R |
J |
E,R |
J |
R |
R |
D |
|
|
1N4934 |
12 |
250 |
D |
D |
R |
R |
J |
E,R |
J |
R |
|
|
1N4934GP |
5 |
100 |
J |
D |
R |
E,R |
D |
R |
J |
R |
|
|
1N4935 |
6 |
150 |
R |
J |
R |
D |
E,R |
D |
R |
J |
|
|
1N4935GP |
7 |
200 |
J |
R |
D |
J |
D |
E,R |
R |
R |
|
|
1N4936 |
8 |
250 |
R |
J |
E,R |
R |
J |
D |
D |
R |
|
|
1N4936GP |
9 |
100 |
R |
R |
D |
J |
R |
J |
E,R |
D |
|
|
1N4937 |
10 |
150 |
D |
R |
J |
R |
J |
R |
D |
E,R |
|
|
1N4937GP |
11 |
200 |
E,R |
D |
R |
R |
R |
J |
J |
D |
|
|
1N4942GP |
12 |
250 |
D |
E,R |
J |
D |
R |
R |
R |
J |
|
|
1N4944GP |
5 |
100 |
D |
R |
-J |
E,R |
R |
J |
D |
R |
|
|
1N4946GP |
6 |
150 |
R |
D |
-J |
R |
E,R |
R |
J |
D |
|
|
1N4947GP |
7 |
200 |
D |
R |
R |
D |
R |
E,R |
J |
J |
|
|
1N4948GP |
8 |
250 |
J |
D |
-E,R |
R |
D |
R |
R |
J |
|
|
1N4001 |
9 |
100 |
J |
J |
R |
D |
R |
D |
E,R |
R |
|
|
1N4001GP |
10 |
150 |
R |
J |
D |
J |
D |
R |
R |
E,R |
|
|
1N4002 |
11 |
200 |
E,R |
R |
R |
J |
J |
D |
D |
R |
|
|
1N4002GP |
12 |
250 |
R |
E,R |
D |
R |
J |
J |
R |
D |
|
|
1N4003 |
5 |
100 |
R |
D |
R |
D |
R |
E,R |
J |
J |
|
|
1N4003GP |
6 |
150 |
J |
R |
-J |
D |
D |
R |
E,R |
R |
|
|
1N4004 |
7 |
200 |
R |
J |
-E,R |
R |
D |
D |
R |
J |
|
|
1N4004GP |
8 |
250 |
J |
R |
R |
J |
R |
D |
D |
E,R |
|
|
1N4005 |
9 |
100 |
E,R |
J |
D |
R |
J |
R |
D |
R |
|
|
1N4005GP |
10 |
150 |
R |
E,R |
D |
J |
R |
J |
R |
D |
|
|
1N4006 |
11 |
200 |
D |
R |
R |
E,R |
J |
R |
J |
D |
|
|
1N4006GP |
12 |
250 |
D |
D |
-J |
R |
E,R |
J |
R |
R |
|
|
1N4007 |
5 |
100 |
J |
D |
-J |
E,R |
D |
R |
R |
R |
|
|
1N4007GP |
6 |
150 |
R |
J |
R |
D |
E,R |
D |
R |
J |
|
|
1N4148 |
7 |
200 |
J |
R |
R |
J |
D |
E,R |
D |
R |
|
|
1N4245GP |
8 |
250 |
R |
J |
D |
R |
J |
D |
E,R |
R |
|
|
1N4246GP |
9 |
100 |
R |
R |
-E,R |
J |
R |
J |
D |
D |
|
|
1N4247GP |
10 |
150 |
D |
R |
D |
R |
J |
R |
J |
E,R |
|
|
1N4248GP |
11 |
200 |
E,R |
D |
-J |
R |
R |
J |
R |
D |
|
|
1N4249GP |
12 |
250 |
D |
E,R |
R |
D |
R |
R |
J |
J |
|
|
1N4383GP |
5 |
100 |
D |
R |
D |
E,R |
R |
J |
J |
R |
|
|
1N4384GP |
6 |
150 |
R |
D |
J |
R |
E,R |
R |
J |
D |
|
|
1N4385GP |
7 |
200 |
D |
R |
J |
D |
R |
-E,R |
R |
J |
|
|
1N4531 |
8 |
250 |
J |
D |
R |
R |
D |
R |
E,R |
J |
|
|
1N4532 |
9 |
100 |
J |
J |
E,R |
D |
R |
D |
R |
R |
|
|
1N4534 |
10 |
150 |
R |
J |
R |
J |
D |
R |
D |
E,R |
|
|
1N4585GP |
11 |
200 |
E,R |
R |
D |
J |
J |
D |
R |
R |
|
|
1N4585GP |
12 |
250 |
R |
E,R |
R |
R |
J |
-J |
D |
D |
|
|
1N4586GP |
5 |
100 |
R |
D |
R |
J |
D |
R |
E,R |
J |
|
|
1N4933 |
6 |
150 |
J |
R |
J |
E,R |
D |
D |
R |
R |
|
|
1N4933GP |
7 |
200 |
R |
J |
E,R |
R |
R |
D |
D |
J |
|
|
1N4934 |
8 |
250 |
J |
R |
R |
D |
J |
R |
D |
E,R |
|
|
1N4934GP |
9 |
100 |
E,R |
J |
D |
D |
R |
-J |
R |
R |
|
|
1N4935 |
10 |
150 |
R |
E,R |
D |
R |
J |
R |
J |
D |
|
|
1N4935GP |
11 |
200 |
D |
R |
R |
J |
E,R |
-J |
R |
D |
|
|
1N4936 |
12 |
250 |
D |
D |
J |
R |
R |
-J |
E,R |
R |
|
|
1N4936GP |
5 |
100 |
J |
D |
J |
R |
E,R |
D |
R |
R |
|
|
1N4937 |
6 |
150 |
R |
J |
R |
R |
D |
-E,R |
D |
J |
|
|
1N4937GP |
7 |
200 |
J |
R |
R |
D |
J |
D |
E,R |
R |
|
|
1N4942GP |
8 |
250 |
R |
J |
D |
E,R |
R |
-J |
D |
R |
|
|
1N4944GP |
9 |
100 |
R |
R |
E,R |
D |
J |
R |
J |
D |
|
|
1N4946GP |
10 |
150 |
D |
R |
D |
J |
R |
-J |
R |
E,R |
|
|
1N4947GP |
11 |
200 |
E,R |
D |
J |
R |
R |
R |
J |
D |
|
|
1N4948GP |
12 |
250 |
D |
E,R |
R |
J |
D |
R |
R |
J |
|
|
1N4001 |
5 |
100 |
D |
R |
D |
J |
E,R |
R |
J |
R |
|
|
1N4001GP |
6 |
150 |
R |
D |
J |
J |
R |
-E,R |
R |
D |
|
|
1N4002 |
7 |
200 |
D |
R |
J |
R |
D |
R |
E,R |
J |
|
|
1N4002GP |
8 |
250 |
J |
D |
R |
E,R |
R |
D |
R |
J |
|
|
1N4003 |
9 |
100 |
J |
J |
E,R |
R |
D |
R |
D |
R |
|
|
1N4003GP |
10 |
150 |
R |
J |
R |
D |
J |
D |
R |
E,R |
|
|
1N4004 |
11 |
200 |
E,R |
R |
D |
R |
J |
-J |
D |
R |
|
|
1N4004GP |
12 |
250 |
R |
E,R |
R |
D |
R |
-J |
J |
D |
|
|
1N4005 |
5 |
100 |
J |
D |
R |
D |
J |
R |
E,R |
R |
|
|
1N4005GP |
6 |
150 |
R |
J |
D |
E,R |
R |
-J |
D |
R |
|
|
1N4006 |
7 |
200 |
R |
R |
E,R |
D |
J |
R |
J |
D |
|
|
1N4006GP |
8 |
250 |
D |
J |
D |
J |
R |
R |
R |
E,R |
План расчета нелинейной цепи методом простой итерации
Нелинейную цепь заменяем линейной: нелинейные элементы заменяем линейными.
Для полученной линейной цепи формируем уравнения по известным методам расчета сложных цепей.
Из полученной системы расчетных уравнений получаем nуравнений в виде функции:
,
(1)
где n - количество нелинейных элементов.
Анализ ВАХ НЭ необходим для того, чтобы при формировании итерационных уравнений итерационный процесс сходился.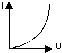
Если ВАХ имеет вид:
.
Если же ВАХ имеет вид :
то итерационные уравнения записываются относительно напряжений на линейном элементе.
,
(2)
5).Полученные уравнения решаются при к=0,1,2,..(шаг итерации).
Итерационный процесс продолжается до тех пор, пока
,
где
- заданная точность.
7)Для
начала решения итерационных уравнений
положим к=0, а
задаем произвольно, но в пределах
видимости ВАХ.