
- •Основные понятия и определения.
- •Условные обозначения и размерность основных величин
- •Основные элементы процесса измерения
- •Классификация измерений
- •Особенности электро-радиоизмерений
- •Основы теории погрешностей и обработки результатов измерений. Классификация погрешностей
- •Классификация погрешностей по форме выражения
- •Классификация погрешностей по причине возникновения.
- •Классификация погрешностей измерений по закономерностям проявления.
- •Математическое описание случайных погрешностей
- •Оценка случайных погрешностей прямых равноточных измерений
- •Суммирование погрешностей
- •Погрешность косвенных измерений
- •Способы оценивания и исключения систематических погрешностей
- •Формы представления результатов измерений и показатели точности
- •Классификация средств измерений Классификация средств измерений по их роли, выполняемой в процессе измерений
- •Классификация средств измерений по роли выполняемые в системе обеспечения единства измерений
- •Классификация средств электроизмерений по измеряемой величине и принципу действия Системы обозначений
- •Классификация методов измерений
- •Структурная схема прямого преобразования
- •Структурная схема прямого преобразования
- •Структурная схема уравновешивающего преобразования
- •Аналоговые и цифровые измерительные приборы Аналоговые приборы
- •Обобщенная структурная схема цифровых измерительных приборов (цип)
- •Общие методы повышения точности средств измерений
- •Классификация измерительных приборов
- •Основные метрологические характеристики средств измерений
- •Выбор методов и средств измерений. Планирование измерений.
- •Выбор средства измерений.
- •Основные правила измерений. Составление схемы измерительной установки.
- •Правила округления значений погрешности и результата наблюдений.
- •Правила построения графиков.
- •Измерение напряжения измерение постоянного напряжения
- •Электронные вольтметры постоянного тока
- •Измерение переменных напряжений.
- •Вольтметры амплитудных значений.
- •Вольтметры среднеквадратических значений.
- •Вольтметры средневыпремленных значений
- •Цифровой вольтметр с временным импульсным преобразователем
- •Специальные типы вольтметров
- •Фазочувствительный вольтметр
- •Избирательные (селективные) вольтметры.
- •Изменение мощности в цепях постоянного тока
- •Измерение мощности в цепях переменного тока
- •Общая характеристика методов измерения мощности на высоких и сверхвысоких частотах
- •Измерение мощности с помощью терморезисторов
- •Калориметрический метод измерения мощности
- •Измерение мощности свч по напряжению, выделяемому на известном сопротивлении
- •Измерители мощности, основанные на использовании пондемоторного (механического) действия электромагнитного поля
- •Измерение проходящей мощности
- •Метод измерения мощности, основанный на эффекте Холла
- •Метод, использующий неоднородный разогрев зарядов в полупроводниках
- •Измерение импульсной мощности
- •Измерение частоты Общие сведения
- •Метод дискретного счета Измерение частоты следования импульсов
- •Измерение частоты гармонического напряжения
- •Уменьшение погрешности дискретности
- •Возможности электронно-счетных частотомеров
- •Гетеродинный метод
- •Сочетание методов дискретного счета и гетеродинного
- •Резонансный метод
- •Метод заряда и разряда конденсатора
- •Методы сравнения с частотой другого источника посредством осциллографа
- •Метод интерференционных фигур
- •Метод круговой развертки с модуляцией яркости
- •Меры частоты
- •Измерение фазового сдвига Общие сведения
- •Фазометр с преобразованием сигналов в прямоугольное напряжение
- •Измерения фазового сдвига с помощью осциллографа
- •Компенсационный метод
- •Измерение фазового сдвига по геометрической сумме и разности напряжений
- •Фазометр с преобразованием фазового сдвига во временной интервал
- •Цифровые фазометры
- •Осциллографы Общие сведения
- •Общая структурная схема и принцип действия электронно-лучевого осциллографа
- •Виды осциллографических разверток
- •Основные узлы электронно-лучевого осциллографа Канал вертикального отклонения
- •Канал горизонтального отклонения
- •Калибраторы
- •Синхронизация развертки
- •Двухканальные и двухлучевые осциллографы
- •Скоростные и запоминающие осциллографы Особенности скоростных осциллографов
- •Стробоскопические осциллографы
- •Запоминающие осциллографы
Суммирование погрешностей
При суммировании погрешностей пользуются:
Систематические погрешности
 если они известны или достаточно точно
определены, суммируют алгебраически
(с учетом знаков)
если они известны или достаточно точно
определены, суммируют алгебраически
(с учетом знаков)

Рекомендуется при суммировании рассматривать все погрешности измерительной аппаратуры как случайные.
Случайные погрешности (среднеквадратические оценки) суммируют с учетом их взаимных коррекционных связей. Среднеквадратическая погрешность
 суммы двух случайных погрешностей
характеризуемых среднеквадратичными
отклонениями
суммы двух случайных погрешностей
характеризуемых среднеквадратичными
отклонениями
 и
и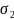 ,
,
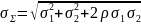
Где

Т.к.
обычно информация о тесноте корреляционных
связей отсутствует, то на практике
рассматриваются 2 крайних случая:
 .
При этом:
.
При этом:
Некоррелированные (вызванные взаимно независимыми источниками или причинами) погрешности суммируются геометрически

Если
количество источников погрешностей n,
то

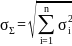
Где
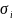 – среднеквадратическая оценка
погрешности, обусловленной -тым
источником.
– среднеквадратическая оценка
погрешности, обусловленной -тым
источником.
Случайные погрешности, сильно или жестко коррелированные (коэффициент корреляции
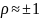 ),
суммируются с учетом следующих
предпосылок. Если причина вызывает в
разных узлах прибора изменение
погрешностей, то погрешности складываются,
т. е.
),
суммируются с учетом следующих
предпосылок. Если причина вызывает в
разных узлах прибора изменение
погрешностей, то погрешности складываются,
т. е.

Когда
же изменения получаются противоположными,
погрешности складываются, т.е.

Суммирование системной погрешности со случайной осуществляют с учетом корреляционных связей по тому же принципу, что и суммирование случайных погрешностей.
Погрешность косвенных измерений
Определение погрешностей функции результатов измерений основывается на двух теоремах теории погрешностей измерений:
Теорема
1: Если величина
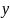 ,
значение которой измеряют косвенным
путем, представляет собой линейную
функцию
,
значение которой измеряют косвенным
путем, представляет собой линейную
функцию
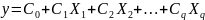 ,
где
,
где
 – независимые результаты прямых
измерений значений аргументов
– независимые результаты прямых
измерений значений аргументов
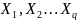 ,
полученные с абсолютными среднеквадратичными
случайными погрешностями
,
полученные с абсолютными среднеквадратичными
случайными погрешностями
 и содержащие соответственно абсолютные
математические погрешности (аддитивные
составляющие)
и содержащие соответственно абсолютные
математические погрешности (аддитивные
составляющие)
 , то результат косвенного измерения,
определяется из формулы
, то результат косвенного измерения,
определяется из формулы
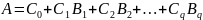 , содержит абсолютную систематическую
погрешность
, содержит абсолютную систематическую
погрешность
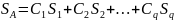 и характеризующуюся абсолютной
среднеквадратичной случайной погрешностью
и характеризующуюся абсолютной
среднеквадратичной случайной погрешностью

При доказательстве этой теоремы предполагается, что погрешности независимы друг от друга и от измеряемых значений.
Теорема
2: Если величина
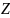 ,
значение которой измеряют косвенным
путем, представляет собой нелинейную
дифференцируемую функцию
,
значение которой измеряют косвенным
путем, представляет собой нелинейную
дифференцируемую функцию
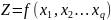 и
и
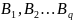 – независимые результаты прямых
измерений значений аргументов
– независимые результаты прямых
измерений значений аргументов
 , полученные с абсолютными
среднеквадратическими случайными
погрешностями
и содержащие соответственно систематические
погрешности
, то результат косвенного измерения,
определяемый из выражения
, полученные с абсолютными
среднеквадратическими случайными
погрешностями
и содержащие соответственно систематические
погрешности
, то результат косвенного измерения,
определяемый из выражения
 ,
содержит абсолютную систематическую
погрешность
,
содержит абсолютную систематическую
погрешность
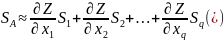 и характеризуется абсолютной
среднеквадратичной случайной погрешностью
и характеризуется абсолютной
среднеквадратичной случайной погрешностью

При
доказательстве теоремы 2 предполагается,
что погрешности независимы друг от
друга и от измеряемых значений, а также
настолько малы, что функция
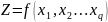 в этих пределах изменения аргументов
может быть линеаризована, т.е. при
разложении функции в ряд Тейлора может
быть учтены только члены первого порядка.
Если случайные погрешности коррелированы,
то
в этих пределах изменения аргументов
может быть линеаризована, т.е. при
разложении функции в ряд Тейлора может
быть учтены только члены первого порядка.
Если случайные погрешности коррелированы,
то
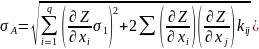
Где
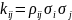 – корреляционный момент случайных
погрешностей
– корреляционный момент случайных
погрешностей
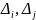
Так
как получение информации о тесноте
корреляционных связей – задача сложная,
то обычно рассматривают 2 крайних случая:
при наличии связи полагают коэффициент
корреляции
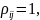 а
если она отсутствует, то
а
если она отсутствует, то

Когда знаки частных системных погрешностей результата косвенных измерений определяют по формуле

Эту
погрешность называют предельной
системной погрешностью. При расчете
относительных погрешностей
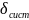 и
и
 вырождения для
вырождения для
 и
и
 относят к результату косвенных измерений
А. Чтобы получить расчетные формулы
правые части (*), (**), (***) после взятия
частных производных делят соответственно
на правые части функции
или
и в полученных выражениях заменяют
аргументы
результатами
измерений.
относят к результату косвенных измерений
А. Чтобы получить расчетные формулы
правые части (*), (**), (***) после взятия
частных производных делят соответственно
на правые части функции
или
и в полученных выражениях заменяют
аргументы
результатами
измерений.
