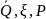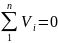- •Основные понятия и определения.
- •Условные обозначения и размерность основных величин
- •Основные элементы процесса измерения
- •Классификация измерений
- •Особенности электро-радиоизмерений
- •Основы теории погрешностей и обработки результатов измерений. Классификация погрешностей
- •Классификация погрешностей по форме выражения
- •Классификация погрешностей по причине возникновения.
- •Классификация погрешностей измерений по закономерностям проявления.
- •Математическое описание случайных погрешностей
- •Оценка случайных погрешностей прямых равноточных измерений
- •Суммирование погрешностей
- •Погрешность косвенных измерений
- •Способы оценивания и исключения систематических погрешностей
- •Формы представления результатов измерений и показатели точности
- •Классификация средств измерений Классификация средств измерений по их роли, выполняемой в процессе измерений
- •Классификация средств измерений по роли выполняемые в системе обеспечения единства измерений
- •Классификация средств электроизмерений по измеряемой величине и принципу действия Системы обозначений
- •Классификация методов измерений
- •Структурная схема прямого преобразования
- •Структурная схема прямого преобразования
- •Структурная схема уравновешивающего преобразования
- •Аналоговые и цифровые измерительные приборы Аналоговые приборы
- •Обобщенная структурная схема цифровых измерительных приборов (цип)
- •Общие методы повышения точности средств измерений
- •Классификация измерительных приборов
- •Основные метрологические характеристики средств измерений
- •Выбор методов и средств измерений. Планирование измерений.
- •Выбор средства измерений.
- •Основные правила измерений. Составление схемы измерительной установки.
- •Правила округления значений погрешности и результата наблюдений.
- •Правила построения графиков.
- •Измерение напряжения измерение постоянного напряжения
- •Электронные вольтметры постоянного тока
- •Измерение переменных напряжений.
- •Вольтметры амплитудных значений.
- •Вольтметры среднеквадратических значений.
- •Вольтметры средневыпремленных значений
- •Цифровой вольтметр с временным импульсным преобразователем
- •Специальные типы вольтметров
- •Фазочувствительный вольтметр
- •Избирательные (селективные) вольтметры.
- •Изменение мощности в цепях постоянного тока
- •Измерение мощности в цепях переменного тока
- •Общая характеристика методов измерения мощности на высоких и сверхвысоких частотах
- •Измерение мощности с помощью терморезисторов
- •Калориметрический метод измерения мощности
- •Измерение мощности свч по напряжению, выделяемому на известном сопротивлении
- •Измерители мощности, основанные на использовании пондемоторного (механического) действия электромагнитного поля
- •Измерение проходящей мощности
- •Метод измерения мощности, основанный на эффекте Холла
- •Метод, использующий неоднородный разогрев зарядов в полупроводниках
- •Измерение импульсной мощности
- •Измерение частоты Общие сведения
- •Метод дискретного счета Измерение частоты следования импульсов
- •Измерение частоты гармонического напряжения
- •Уменьшение погрешности дискретности
- •Возможности электронно-счетных частотомеров
- •Гетеродинный метод
- •Сочетание методов дискретного счета и гетеродинного
- •Резонансный метод
- •Метод заряда и разряда конденсатора
- •Методы сравнения с частотой другого источника посредством осциллографа
- •Метод интерференционных фигур
- •Метод круговой развертки с модуляцией яркости
- •Меры частоты
- •Измерение фазового сдвига Общие сведения
- •Фазометр с преобразованием сигналов в прямоугольное напряжение
- •Измерения фазового сдвига с помощью осциллографа
- •Компенсационный метод
- •Измерение фазового сдвига по геометрической сумме и разности напряжений
- •Фазометр с преобразованием фазового сдвига во временной интервал
- •Цифровые фазометры
- •Осциллографы Общие сведения
- •Общая структурная схема и принцип действия электронно-лучевого осциллографа
- •Виды осциллографических разверток
- •Основные узлы электронно-лучевого осциллографа Канал вертикального отклонения
- •Канал горизонтального отклонения
- •Калибраторы
- •Синхронизация развертки
- •Двухканальные и двухлучевые осциллографы
- •Скоростные и запоминающие осциллографы Особенности скоростных осциллографов
- •Стробоскопические осциллографы
- •Запоминающие осциллографы
Математическое описание случайных погрешностей
Измеряемая величина это случайная величина. Наиболее общей характеристикой непрерывной случайной величины является плотность распределения её вероятности, которая определяется как
 ,где
dF(x)
– вероятность значений случайной
величины x в
интервале dx.
,где
dF(x)
– вероятность значений случайной
величины x в
интервале dx.
Кроме этого используется функция распределения вероятностей случайной величины
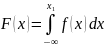
которая
выражает собой вероятность того, что
случайная величина находится в интервале
от
 до некоторого значения <x1
до некоторого значения <x1
Функция
распределения любой случайной величины
является неубывающей функцией,
определенной так, что
 .
Вероятность того, что случайная величина
x примет значение
в интервале между x1
и x2 равна
.
Вероятность того, что случайная величина
x примет значение
в интервале между x1
и x2 равна

В практике электроизмерений чаще всего имеют дело с нормальным и равномерным распределениями.
Случайная
величина
 распределена нормально, если её плотность
вероятностей имеет вид
распределена нормально, если её плотность
вероятностей имеет вид

где
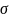 – среднее квадратическое отклонение
(СКО)
– среднее квадратическое отклонение
(СКО)
 – математическое
ожидание
– математическое
ожидание
Оценка случайных погрешностей прямых равноточных измерений
Случайные погрешности проявляются при многократных наблюдениях измеряемой величины в одинаковых условиях, их влияние на результат измерения надо учитывать и стремиться по возможности уменьшить.
К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности.
Оценка
параметра Q считается
состоятельной, если
 , несмещенной, если
, несмещенной, если
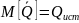 , эффективной, если
, эффективной, если
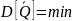 . Здесь
. Здесь
 – результат i-того
наблюдения n – число
наблюдений.
– результат i-того
наблюдения n – число
наблюдений.
Способы нахождения оценок конечного ряда наблюдений и показатели их качества зависит от законов распределения.
Для нормального распределения, а если пренебречь эффективностью оценки, то и для всех симметричных распределений, в качестве оценки математического ожидания ряда равноточных наблюдений принимают среднее арифметическое ряда наблюдений.
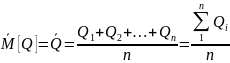
При
 ,
если нет систематических погрешностей,
,
если нет систематических погрешностей,
 . Разность
. Разность
 представляет собой случайную погрешность
при i-том наблюдении.
Она может быть положительной и
отрицательной.
представляет собой случайную погрешность
при i-том наблюдении.
Она может быть положительной и
отрицательной.
Среднее арифметическое независимо от закона распределения, обладает следующими свойствами:
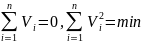
В качестве оценки дисперсии берется дисперсия отклонения результата наблюдения
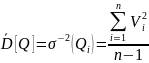
А в качестве оценки СКО результата наблюдения –
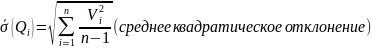
Широко
используется понятие максимальной
погрешности, под которой понимают закон
трех сигм. Так как на практике число
измерений не превышает несколько
десятков, то появление погрешности
равно
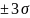 ,
маловероятно. Потому погрешность
– максимальная возможная случайная
погрешность. Погрешности больше
считаются промахами и при обработке
результатов измерений не учитываются.
Схема обработки результатов измерения
с многократными измерениями:
,
маловероятно. Потому погрешность
– максимальная возможная случайная
погрешность. Погрешности больше
считаются промахами и при обработке
результатов измерений не учитываются.
Схема обработки результатов измерения
с многократными измерениями:
Оценка
закона распределения
n
наблюдений


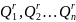


Выбор доверительной вероятности Р
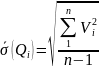
Исключение
систематических погрешностей


Оценка доверительного интервала

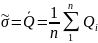
Запись
результата
Проверка
Остаточные
погрешности