48. Выражение тока, напряжения, сопротивления, проводимости, эдс электромагнитной индукции, мощности комплексными числами. Законы Ома и Кирхгофа в символическом виде.

• Выражение тока, напряжения, сопротивления, проводимости, ЭДС электромагнитной индукции, мощности комплексными числами

• Законы Ома и Кирхгофа в символическом виде

49. Комплексная передаточная функция. Частотные характеристики. Ачх, фчх. Годограф. Частотные характеристики простейших двухполюсников.

• Комплексная передаточная функция

• Частотные характеристики. АЧХ, ФЧХ

• Годограф

50. Понятие о колебательном контуре. Свободные колебания в идеальном контуре. Период, частота и длина волны свободных колебаний. Характеристическое сопротивление контура. Свободные колебания в реальном контуре. Затухание колебаний. Добротность контура.

• Колебательный контур

Представляет собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи может возбуждаться колебания тока и напряжения.

• Свободные колебания в идеальном контуре

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур.

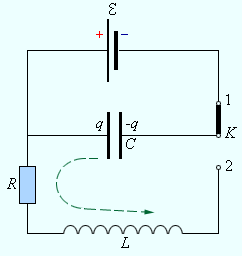
• Характеристическое сопротивление контура

Отношение амплитуды напряжения на конденсаторе или равной ей амплитуды э.д.с. самоиндукции на катушке к амплитуде тока в колебательном контуре при последовательном резонансе. Также называют волновым сопротивлением контура.

• Свободные колебания в реальном контуре

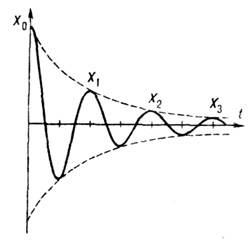
• Затухание колебаний

Уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебат. системой.

• Добротность контура

Характеризует качество колебательного контура, обозначается Q. Численно равна отношению напряжения на любом из реактивных участков на резонансе к напряжению, подводимому к контуру, или отношению реактивного сопротивления к активному. При большой добротности контура напряжение на нем значительно превышает напряжение на входе контура.

51. Последовательный колебательный контур. Вынужденные колебания. Полное сопротивление контура, его составляющие и зависимость их от частоты. Резонанс напряжений, условие его возникновения. Признаки резонанса. Резонансная частота. Векторная диаграмма.

• Последовательный колебательный контур

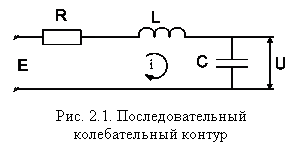
52. Последовательный колебательный контур. Коэффициент мощности. Коэффициент передачи по напряжению. Добротность. Амплитудно-частотные и фазочастотные характеристики.

• Коэффициент мощности

Безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

• Коэффициент передачи по напряжению

Коэффициент передачи (также коэффициент преобразования) — отношение напряжения на выходе той или иной системы, предназначенной для передачи электрических сигналов, к напряжению на входе. В частном случае, когда значения выходного и входного сигнала являются однородными, коэффициент передачи называют коэффициентом усиления. KП = UВЫХ / UВХ. Коэффициент передачи часто выражают в логарифмическом виде, как 20 lg (UВЫХ / UВХ), дБ

• Добротность

Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Общая формула для добротности любой колебательной системы:

,

где:

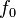•  — резонансная частота колебаний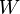

•  — энергия, запасённая в колебательной системе

•  — рассеиваемая мощность.

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.

• Амплитудно-частотные и фазочастотные характеристики