37. Интегрирующая и дифференцирующая цепи.

• Интегрирующая цепь

Выходным напряжением в интегрирующей цепи является напряжение на конденсаторе. Естественно, если конденсатор разряжен, оно равно нулю. При подаче импульса напряжения на вход цепи конденсатор начнет накапливать заряд, и накопление будет происходить по экспоненциальному за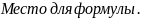 кону, соответственно, и напряжение на нем будет нарастать по экспоненте от нуля до своего максимального значения. Его значение можно определить по формуле U_вых = U₀(1 - e^-t/τ). Постоянная времени цепи определяется по такой же формуле, как и для дифференцирующей цепи и имеет тот же смысл.

• Дифференцирующая цепь

Вот такое соединение резистора и конденсатора называется дифференцирующей цепью или укорачивающей цепью. На графиках показаны эпюры напряжения на входе и выходе этой цепи. Допустим, что конденсатор разряжен. При подаче на вход RC-цепи импульса напряжения конденсаторе сразу же начнет заряжаться током, проходящим через него самого и резистор. Сначала ток будет максимальным, затем по мере увеличения заряда конденсатора постепенно уменьшится до нуля по экспоненте. Когда через резистор проходит ток, на нем образуется падение напряжения, которое определяется, как U=i R, где i-ток заряда конденсатора. Поскольку ток изменяется экспоненциально, то и напряжение будет изменяться также - экспоненциально от максимума до нуля. Падение напряжения на резисторе как раз таки и является выходным. Его величину можно определить по формуле U_вых = U₀e^-t/τ. Величина τ называется постоянной времени цепи и соответствует изменению выходного напряжения на 63% от исходного (e^-1 = 0.37). Очевидно, что время изменения выходного напряжения зависит от сопротивления резистора и емкости конденсатора и, соответственно, постоянная времени цепи пропорциональна этим значениям, т. е. τ = RC. Если емкость в Фарадах, сопротивление в Омах, то τ в секундах.

38. Цепь синусоидального тока с емкостью. Закон Ома для действующих и амплитудных значений тока и напряжения. Ёмкостное сопротивление, его зависимость от частоты.

• Цепь синусоидального тока с емкостью

• Закон Ома для действующих и амплитудных значений тока и напряжения

• Ёмкостное сопротивление, его зависимость от частоты.

Величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью цепи (или её участка). Ёмкостное сопротивление синусоидальному току Хс = 1/ωС, где ω — угловая частота, С — ёмкость. Измеряется в омах.

39. Цепь синусоидального тока с емкостью. Энергетический процесс. Мгновенная, активная и реактивная мощности.

• Энергетический процесс

• Мгновенная, активная и реактивная мощности

40. Последовательное соединение резистора и конденсатора (конденсатор с потерями). Временная и векторная диаграммы. Закон Ома для действующих и амплитудных значений тока и напряжения.

Для увеличения ёмкости конденсаторы соединяются параллельно

41. Треугольники напряжений и сопротивлений. Полное сопротивление. Угол сдвига фаз между напряжением и током. Закон Ома для действующих и амплитудных значений тока и напряжения.

• Треугольники напряжений и сопротивлений

• Полное сопротивление (Z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного. 

Здесь:

- активное сопротивление

-емкостное сопротивление

-индуктивное сопротивление

-полное сопротивление, определяет силу тока в цепи по закону Ома

• Угол сдвига фаз между напряжением и током

Угол сдвига фаз между током и напряжением при резонансе равен нулю.

Если угол сдвига фаз между напряжением источника и током равен нулю, то внешняя цепь оказывает источнику сопротивление чисто активного характера. В данном случае напряжение U и ток / 0 совпадают по фазе и, следовательно, колебательный контур ведет себя по отношению к источнику как активное сопротивление.

Угол сдвига фаз между током и напряжением зависит от соотношения между активным и реактивным сопротивлениями, включенными в цепь.

Угол сдвига фаз между напряжением и током определяется непосредственно на диаграмме.

42. Энергетический процесс. Мгновенная, активная, реактивная и полная мощности. Треугольник мощностей. Коэффициент мощности.

• Энергетический процесс

• Мгновенная, активная, реактивная и полная мощности

1. Мгновенная мощность

Мгновенная мощность P_R = u_Ri содержит две составляющие: постоянную и переменную, которая изменяется по закону косинуса с частотой 

2. Активная мощность

Среднее за период значение мгновенной мощности (называется активной мощностью) равно:

3. Реактивная мощность

4. Полная мощность

Полная мощность определяется по формуле: лишь в том случае, если спектры тока и напряжения совпадают. При несовпадении спектров этих функций:

, где T – мощность искажения, обусловленная несовпадением спектров тока и напряжения.

• Треугольник мощностей

Треугольник мощностей – это графическое изображение активной, реактивной и полной мощностей в цепи переменного тока.

Треугольник мощностей получается из соотношения Р² + Q² = S²

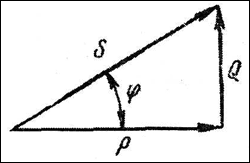
• Коэффициент мощности

Безразмерная физическая величина. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

43. Последовательное соединение активного, индуктивного и ёмкостного сопротивлений. II закон Кирхгофа для мгновенных значений. Временная и векторная диаграммы для различного характера цепи.

• Последовательное соединение активного, индуктивного и ёмкостного сопротивлений.